京改版数学八年级上册课件 11.4 无理数与实数(1)(共31张ppt)
文档属性
| 名称 | 京改版数学八年级上册课件 11.4 无理数与实数(1)(共31张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 21:47:27 | ||
图片预览










文档简介
(共31张PPT)
无理数与实数(1)
初二年级
数学
整数和分数统称为有理数
古希腊的毕达哥拉斯学派曾断言:“世界上只有整数和分数,除此之外,就再也没有别的什么数了.”
这个断言正确吗?
新课引入
1.面积等于2的正方形的边长是
;
2.体积等于5的正方体的棱长是
.
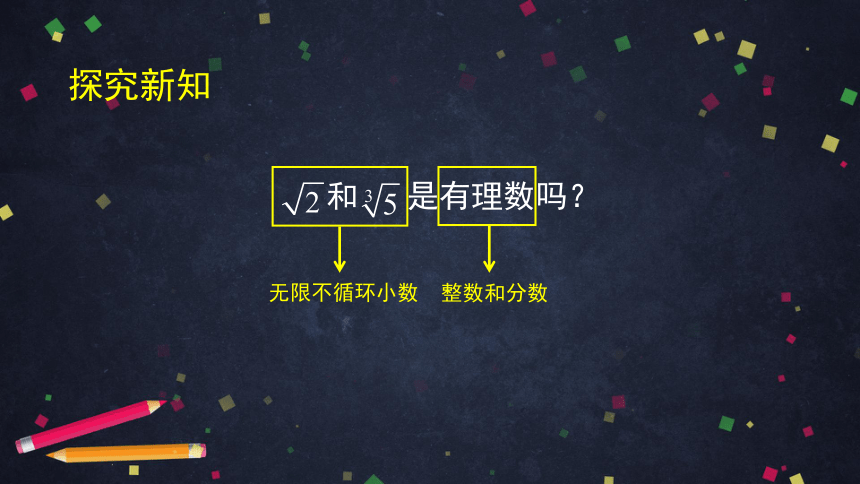
探究新知
和
是有理数吗?
可以借助科学计算器进行探究.
探究新知
用计算器计算:
=
.
计算器屏幕上显示出的有限小数是
的精确值吗?
1.414
213
562
按键
输入:2
按键
显示:
1.414
213
562
373
095
探究新知
用计算器计算:
(1)1.414
2132
=
(2)1.414
213
5622
=
(3)1.414
213
562
3732
=
1.999
999
998
944
727
844
1.999
999
999
999
731
161
391
129
1.999
998
409
369
;
;
.
有限小数只是
的近似值.
……
探究新知
是一个无限不循环小数.
=
1.414
213
562
373???
它的小数点后面的位数是无限的,而且是不循环的.
探究新知
也是一个无限不循环小数.
用计算器计算:
=
1.709
975
9463
=
1.709
975
946
???
4.999
999
994
063
978
001
557
890
536
;
.
探究新知
整数和分数
无限不循环小数
和
是有理数吗?
探究新知
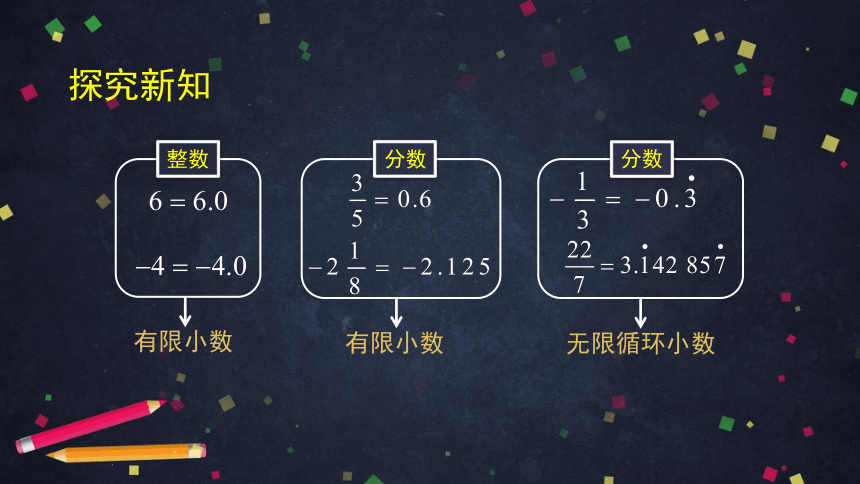
请把下列有理数写成小数形式,观察它们的小数部分各有什么特点?
整数
分数
,
,
,
,
,
.
探究新知
有限小数
无限循环小数
有限小数
整数
分数
分数
探究新知
无限循环小数
小数点后是0的有限小数
有理数
有限小数
任意有理数都可以用有限小数或无限循环小数表示;反过来,有限小数或无限循环小数也都是有理数.
整数
分数
归纳总结
探究新知
无限不循环小数不是有理数.
无限不循环小数
和
是有理数吗?
和
不是有理数.
有限小数或无限循环小数
探究新知
3.141
592
653…
.
π
1.732
050
807…,
无限不循环小数有很多,类似的还有:
2.236
067
977…,
?7.280
109
889…,
……
探究新知
无理数的概念:无限不循环小数叫做无理数.
无理数的本质特征:
①
无限小数;
②
不循环小数.
两个本质特征缺一不可.
概念讲解
下列各数中,哪些是无理数?
(两个1之间依次多一个2)
化简得4
有理数
无理数
有限小数
有理数
无理数
无限循环小数
有理数
,
,
,
,
,?0.121
221
222
1…
.
,
,?0.121
221
222
1…是无理数.
.
无理数
概念理解
无理数的三种常见形式:
①带根号且开方开不尽的数,如:
,
;
②π以及含π的代数式,如:
,
;
③特殊的无限不循环小数,如:0.121
221
222
1….
归纳总结
判断正误:
①无限小数一定是无理数;
②无理数是无限小数;
③带根号的数一定是无理数;
④无理数是带根号的数.
错误
正确
错误
错误
反例:
,
,
.
无限循环小数
无限不循环小数
反例:
π,0.121
221
222
1….
反例:0.3
.
.
概念辨析
概
念
有理数
整数和分数
(有限小数或无限循环小数)
无理数
无限不循环小数
?
在数轴上表示
任意一个有理数都
能用数轴上的点表示
知识对比
你能在数轴上找到表示
的点吗?
分析:
可以表示面积等于2的正方形的边长.
思考:如何作一个面积等于2的正方形呢?
再探新知
从如图所示的折纸中(正方形纸片边长为2),你能不能得到启发?
原正方形的面积为4;
黄色正方形的面积为2;
黄色正方形的边长为
.
再探新知
也可以表示边长为1的正方形的对角线长.
从如图所示的折纸中(正方形纸片边长为2),你还能得到什么启发?
O
A
B
C
可以表示面积为2的正方形的边长;
再探新知
在数轴上作出表示
的点.
作法:在数轴Ox上以1个单位长度的线段OA为一边作正方形OABC,连接OB;
再探新知
O
1
2
x
-
1
A
B
C
作法:在数轴Ox上以1个单位长度的线段OA为一边作正方形OABC,连接OB;
在Ox轴上截取线段OD=OB,所以OD=
,点D所对应的数便是
.
在数轴上作出表示
的点.
再探新知
O
1
2
x
-
1
A
B
C
D
事实上,每个无理数都可以用数轴上的一个点表示.数轴上的点,有的表示有理数,有的表示无理数.
归纳总结
学习了无理数的概念和在数轴上表示.
课堂小结
概
念
有理数
整数和分数
(有限小数或无限循环小数)
无理数
无限不循环小数
在数轴上表示
任意一个有理数都
能用数轴上的点表示
任意一个无理数都
能用数轴上的点表示
课堂小结
古希腊的毕达哥拉斯学派曾断言:“世界上只有整数和分数,除此之外,就再也没有别的什么数了.”
这个断言正确吗?
错误
希帕索斯
发现了
不是有理数
引发了第一次数学危机
问题解决
1.
下列各数中,哪些是有理数?哪些是无理数?
2.“形如
,
的数是无理数”,这个说法对吗?为什么?
(两个1之间依次多一个0)
,
,
,
,
,
,
,
,?0.101
001
000
1….
课后练习
4.
把直径为1个单位长度的圆放在数轴上从原点向右滚动一周,
圆上的一点O由原点到达另一个点P,这个点P对应的数是多少?
3.
在数轴上找到表示?
的点.
课后练习
祝同学们学习进步!
无理数与实数(1)
初二年级
数学
整数和分数统称为有理数
古希腊的毕达哥拉斯学派曾断言:“世界上只有整数和分数,除此之外,就再也没有别的什么数了.”
这个断言正确吗?
新课引入
1.面积等于2的正方形的边长是
;
2.体积等于5的正方体的棱长是
.
探究新知
和
是有理数吗?
可以借助科学计算器进行探究.
探究新知
用计算器计算:
=
.
计算器屏幕上显示出的有限小数是
的精确值吗?
1.414
213
562
按键
输入:2
按键
显示:
1.414
213
562
373
095
探究新知
用计算器计算:
(1)1.414
2132
=
(2)1.414
213
5622
=
(3)1.414
213
562
3732
=
1.999
999
998
944
727
844
1.999
999
999
999
731
161
391
129
1.999
998
409
369
;
;
.
有限小数只是
的近似值.
……
探究新知
是一个无限不循环小数.
=
1.414
213
562
373???
它的小数点后面的位数是无限的,而且是不循环的.
探究新知
也是一个无限不循环小数.
用计算器计算:
=
1.709
975
9463
=
1.709
975
946
???
4.999
999
994
063
978
001
557
890
536
;
.
探究新知
整数和分数
无限不循环小数
和
是有理数吗?
探究新知
请把下列有理数写成小数形式,观察它们的小数部分各有什么特点?
整数
分数
,
,
,
,
,
.
探究新知
有限小数
无限循环小数
有限小数
整数
分数
分数
探究新知
无限循环小数
小数点后是0的有限小数
有理数
有限小数
任意有理数都可以用有限小数或无限循环小数表示;反过来,有限小数或无限循环小数也都是有理数.
整数
分数
归纳总结
探究新知
无限不循环小数不是有理数.
无限不循环小数
和
是有理数吗?
和
不是有理数.
有限小数或无限循环小数
探究新知
3.141
592
653…
.
π
1.732
050
807…,
无限不循环小数有很多,类似的还有:
2.236
067
977…,
?7.280
109
889…,
……
探究新知
无理数的概念:无限不循环小数叫做无理数.
无理数的本质特征:
①
无限小数;
②
不循环小数.
两个本质特征缺一不可.
概念讲解
下列各数中,哪些是无理数?
(两个1之间依次多一个2)
化简得4
有理数
无理数
有限小数
有理数
无理数
无限循环小数
有理数
,
,
,
,
,?0.121
221
222
1…
.
,
,?0.121
221
222
1…是无理数.
.
无理数
概念理解
无理数的三种常见形式:
①带根号且开方开不尽的数,如:
,
;
②π以及含π的代数式,如:
,
;
③特殊的无限不循环小数,如:0.121
221
222
1….
归纳总结
判断正误:
①无限小数一定是无理数;
②无理数是无限小数;
③带根号的数一定是无理数;
④无理数是带根号的数.
错误
正确
错误
错误
反例:
,
,
.
无限循环小数
无限不循环小数
反例:
π,0.121
221
222
1….
反例:0.3
.
.
概念辨析
概
念
有理数
整数和分数
(有限小数或无限循环小数)
无理数
无限不循环小数
?
在数轴上表示
任意一个有理数都
能用数轴上的点表示
知识对比
你能在数轴上找到表示
的点吗?
分析:
可以表示面积等于2的正方形的边长.
思考:如何作一个面积等于2的正方形呢?
再探新知
从如图所示的折纸中(正方形纸片边长为2),你能不能得到启发?
原正方形的面积为4;
黄色正方形的面积为2;
黄色正方形的边长为
.
再探新知
也可以表示边长为1的正方形的对角线长.
从如图所示的折纸中(正方形纸片边长为2),你还能得到什么启发?
O
A
B
C
可以表示面积为2的正方形的边长;
再探新知
在数轴上作出表示
的点.
作法:在数轴Ox上以1个单位长度的线段OA为一边作正方形OABC,连接OB;
再探新知
O
1
2
x
-
1
A
B
C
作法:在数轴Ox上以1个单位长度的线段OA为一边作正方形OABC,连接OB;
在Ox轴上截取线段OD=OB,所以OD=
,点D所对应的数便是
.
在数轴上作出表示
的点.
再探新知
O
1
2
x
-
1
A
B
C
D
事实上,每个无理数都可以用数轴上的一个点表示.数轴上的点,有的表示有理数,有的表示无理数.
归纳总结
学习了无理数的概念和在数轴上表示.
课堂小结
概
念
有理数
整数和分数
(有限小数或无限循环小数)
无理数
无限不循环小数
在数轴上表示
任意一个有理数都
能用数轴上的点表示
任意一个无理数都
能用数轴上的点表示
课堂小结
古希腊的毕达哥拉斯学派曾断言:“世界上只有整数和分数,除此之外,就再也没有别的什么数了.”
这个断言正确吗?
错误
希帕索斯
发现了
不是有理数
引发了第一次数学危机
问题解决
1.
下列各数中,哪些是有理数?哪些是无理数?
2.“形如
,
的数是无理数”,这个说法对吗?为什么?
(两个1之间依次多一个0)
,
,
,
,
,
,
,
,?0.101
001
000
1….
课后练习
4.
把直径为1个单位长度的圆放在数轴上从原点向右滚动一周,
圆上的一点O由原点到达另一个点P,这个点P对应的数是多少?
3.
在数轴上找到表示?
的点.
课后练习
祝同学们学习进步!
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
