北师大版数学九年级上册6.3反比例函数的应用 专项强化训练(word版含答案)
文档属性
| 名称 | 北师大版数学九年级上册6.3反比例函数的应用 专项强化训练(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 83.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 21:03:08 | ||
图片预览



文档简介
【反比例函数的应用】期末复习专项强化训练(二)
1.某市计划建设一项水利工程,运输公司接到任务后,计划每天运输土方2000m3,共计50天运完,但由于受到各种因素的影响,实际平均每天运输土方vm3,共计t天运输完成.
(1)请直接写出v关于t的函数关系式;
(2)为了给后续工程节省出时间,这批土方需要在40天内运输完成,求实际平均每天至少需要比原计划增加
多少土方运输量?
2.如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m,设AD的长为xm,DC的长为ym.
(1)求y与x之间的函数关系式;
(2)根据实际情况,对于(1)式中的函数自变量x能否取值为4m,若能,求出y的值,若不能,请说明理由;
(3)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案.
3.强哥驾驶小汽车(出租)匀速地从如皋火车站送客到南京绿口机场,全程为280km,设小汽车的行驶时间为t(单位:h),行驶速度为v(单位:km/h),且全程速度限定为不超过120km/h.
(1)求v关于t的函数解析式;
(2)强哥上午8点驾驶小汽车从如皋火车站出发.
①乘客需在当天10点48分至11点30分(含10点48分和11点30分)间到达南京绿口机场,求小汽车行驶速度v的范围;
②强哥能否在当天10点前到达绿口机场?说明理由.
4.某校举行田径运动会,学校准备了某种气球,这些气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求这个函数的表达式;
(2)当气球内的气压大于150kPa时,气球将会爆炸,为了安全起见,气体的体积应至少是多少?
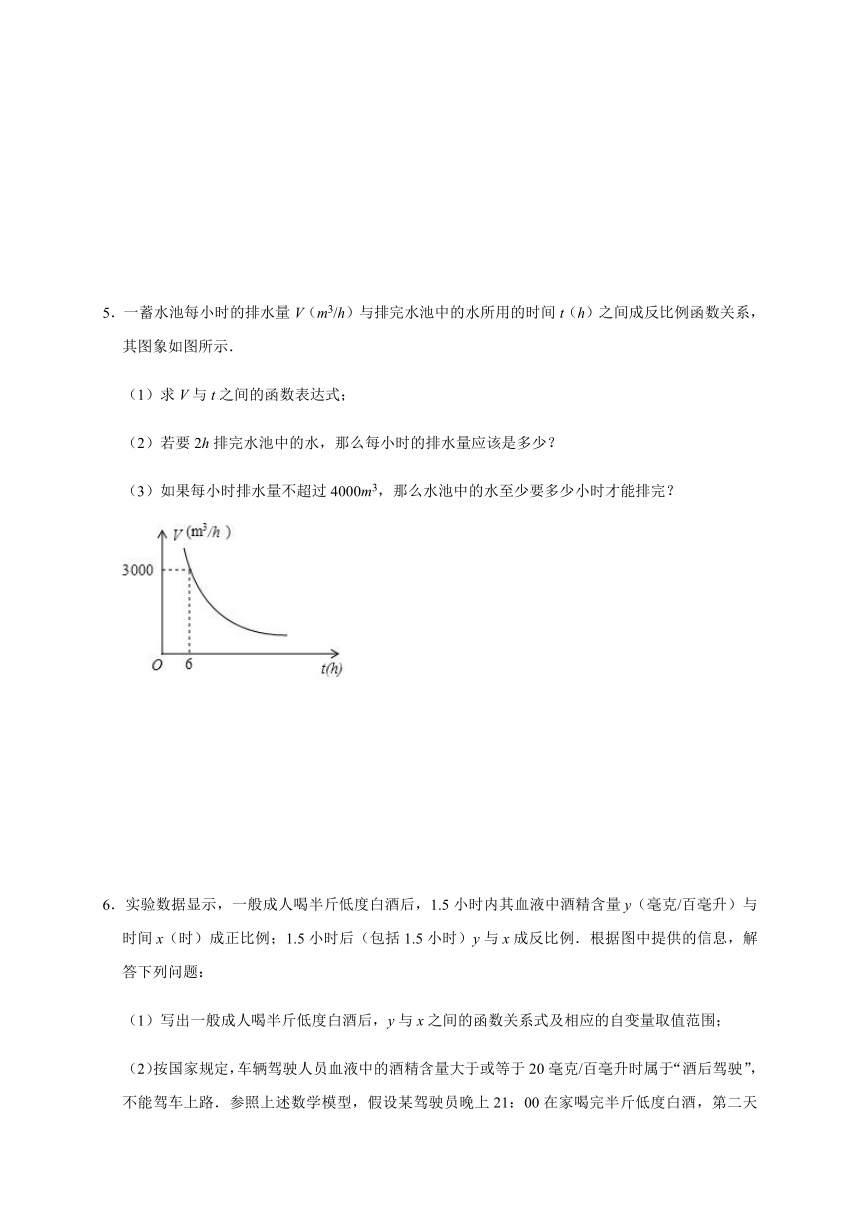
5.一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间成反比例函数关系,其图象如图所示.
(1)求V与t之间的函数表达式;
(2)若要2h排完水池中的水,那么每小时的排水量应该是多少?
(3)如果每小时排水量不超过4000m3,那么水池中的水至少要多少小时才能排完?
6.实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)成正比例;1.5小时后(包括1.5小时)y与x成反比例.根据图中提供的信息,解答下列问题:
(1)写出一般成人喝半斤低度白酒后,y与x之间的函数关系式及相应的自变量取值范围;
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上21:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
7.初中老师在讲授某一次实验中,测得两个变量之间的关系如下表所示:
自变量x
1
2
3
4
12
因变量y
0.12
0.06
0.03
0.015
0.01
请你根据表格回答下列问题:
(1)这两个变量之间可能是怎样的函数关系?你是怎样作出判断的?请你简要说明理由;
(2)请你写出这个函数的解析式;
(3)表格中空缺的数值可能是多少?请你给出合理的数值.
8.某电厂有5000吨电煤.
(1)求:这些电煤能够使用的天数x(单位:天)与该厂平均每天用煤吨数y(单位:吨)之间的函数关系;
(2)若平均每天用煤200吨,则这批电煤能用多少天?
(3)若该电厂前10天每天用200吨,后因各地用电紧张,每天用电煤300吨,则这批电煤共可用多少天?
9.某市蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽植一种在自然光照且温度为18℃的条件下生长最快的新品种蔬菜,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(h)变化的函数图象.其中BC段是双曲线的一部分.根据图中信息解答下列问题:
(1)求BC段双曲线对应的函数表达式.
(2)当时间为16h时,大棚内的温度约为多少度?
10.如图,在平面直角坐标系xOy中,函数(x<0)的图象经过点A(﹣4,n),AB⊥x轴于B,点C与点A关于原点O对称,CD⊥x轴于D,△ABD的面积为8.
(1)求m、n的值.
(2)若直线y=kx+b(k≠0)经过点C,且与x轴、y轴分别交于点E、F.当CF=2CE时,求点F的坐标.
(3)将线段OA绕着点P(1,s)旋转180°,O、A的对应点分别是O1、A1.若O1、A1在同一双曲线上,则s=
.
参考答案
1.解:(1)由题意得:v==;
(2)当t=40时,v==2500,
2500﹣2000=500(m3),
答:实际平均每天至少需要比原计划增加500m3土方运输量.
2.解:(1)由题意得,S矩形ABCD=AD×DC=xy,
故y=.(5≤x)
(2)不能.当x=4时,y=15>12,不合题意;
(3)由y=,且x、y都是正整数,
可得x可取1,2,3,4,5,6,10,12,15,20,30,60,
∵2x+y≤26,0<y≤12,
∴符合条件的围建方案为:AD=5m,DC=12m或AD=6m,DC=10m或AD=10m,DC=6m.
3.解:(1)∵vt=280,且全程速度限定为不超过120千米/小时,
∴v关于t的函数表达式为:v=,(t≥).
(2)①8点至10点48分时间长为小时,8点至11点30分时间长为3.5小时
将t=3.5代入v=得v=80;将t=代入v=得v=100,
∴小汽车行驶速度v的范围为:80≤v≤100;
②强哥不能在当天10点前到达绿口机场.理由如下:
8点至10点前时间长为2小时,将t=2代入v=得v=140>120千米/小时,超速了.
故强哥不能在当天10点前到达绿口机场.
4.解:(1)设P=,将A(0.5,120)代入求出k=60,
∴P=;
(2)当P>150KPa时,气球将爆炸,
∴P≤150,即P=≤150,
解得V≥=0.4(m3).
故为了安全起见,气体的体积应不小于0.4(m3).
5.解:(1)设函数表达式为V=,把(6,3000)代入V=,
得3000=.
解得:k=18000,所以V与t之间的函数表达式为:V=;
(2)把t=2代入V=,得V=9000,
答:每小时的排水量应该是9
000
m3;
(3)把V=4
000代入V=,得t=4.5,
根据反比例函数的性质,V随t的增大而减小,因此水池中的水至少要4.5
h才能排完.
6.解:(1)由题意可得:当0≤x≤1.5时,设函数关系式为:y=kx,
则150=1.5k,
解得:k=100,
故y=100x,
当1.5≤x时,设函数关系式为:y=,
则a=150×1.5=225,
解得:a=225,
故y=(x≥1.5),
综上所述:y与x之间的两个函数关系式为:y=;
(2)第二天早上7:00不能驾车去上班.
理由:∵晚上21:00到第二天早上7:00,有10小时,
∴x=10时,y==22.5>20,
∴第二天早上7:00不能驾车去上班.
7.解:(1)由表中自变量x和因变量y的数值可知:
自变量x和因变量y的乘积都等于0.12,且随着自变量x值的逐渐增加,因变量y的值逐渐减少,故两个变量x和y之间可能是反比例函数关系.
(2)∵两自变量的乘积等于0.12,且两自变量为反比例函数关系,
∴y=;
(3)将x=3代入得:y=0.04;
将y=0.015代入得:x=8;
故答案为:8,0.04.
8.解:(1)由题意可得:y=;
(2)把x=200代入y=,
得y=25.
故这批电煤能用25天.
(3)前10天后还剩下5000﹣10×200=3000(吨)电煤,
可以用=10(天),故共可用20天.
9.解:(1)双曲线y=经过B(12,18),
∴18=,解得k=216.
∴故BC段的函数表达式为:y=;
(2)当x=16时,y==13.5.
答:当x=16时,大棚内的温度约为13.5度.
10.解:(1)∵A、C关于原点对称,
∴C(4,﹣n),
∵S△ABD=×8×(﹣n)=8,n=﹣2,
∴A(﹣4,﹣2),
∴m=8;
(2)由(1)得点C的坐标为C(4,2).
①如图1中,当k<0时,设直线y=kx+b与x轴,y轴的交点分别为点E1,F1.
由
CD⊥x轴于点D可得CD∥OF1.
∴△E1CD∽△E1F1O.
∴=,
∵CF1=2CE1,
∴=,
∴OF1=3DC=6,
∴点F1的坐标为F1(0,6).
②如图2,当k>0时,设直线y=kx+b与x轴,y轴的交点分别为点E2,F2.
同理可得CD∥OF2,=,
∵CF2=2CE2,
∴E2为线段CF2的中点,E2C=E2F2,
∴OF2=DC=2.
∴点F2的坐标为(0,﹣2).
综上所述,点F的坐标为(0,6)或(0,﹣2);
(3)∵将线段OA绕着点P(1,s)旋转180°,O、A的对应点分别是O1、A1.
∴O1(2,2s)、A1(6,2s+2),
∵O1、A1在同一双曲线上,
∴2×2s=6(2s+2),
解得:s=﹣.
故答案为:﹣.
1.某市计划建设一项水利工程,运输公司接到任务后,计划每天运输土方2000m3,共计50天运完,但由于受到各种因素的影响,实际平均每天运输土方vm3,共计t天运输完成.
(1)请直接写出v关于t的函数关系式;
(2)为了给后续工程节省出时间,这批土方需要在40天内运输完成,求实际平均每天至少需要比原计划增加
多少土方运输量?
2.如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m,设AD的长为xm,DC的长为ym.
(1)求y与x之间的函数关系式;
(2)根据实际情况,对于(1)式中的函数自变量x能否取值为4m,若能,求出y的值,若不能,请说明理由;
(3)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案.
3.强哥驾驶小汽车(出租)匀速地从如皋火车站送客到南京绿口机场,全程为280km,设小汽车的行驶时间为t(单位:h),行驶速度为v(单位:km/h),且全程速度限定为不超过120km/h.
(1)求v关于t的函数解析式;
(2)强哥上午8点驾驶小汽车从如皋火车站出发.
①乘客需在当天10点48分至11点30分(含10点48分和11点30分)间到达南京绿口机场,求小汽车行驶速度v的范围;
②强哥能否在当天10点前到达绿口机场?说明理由.
4.某校举行田径运动会,学校准备了某种气球,这些气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求这个函数的表达式;
(2)当气球内的气压大于150kPa时,气球将会爆炸,为了安全起见,气体的体积应至少是多少?
5.一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间成反比例函数关系,其图象如图所示.
(1)求V与t之间的函数表达式;
(2)若要2h排完水池中的水,那么每小时的排水量应该是多少?
(3)如果每小时排水量不超过4000m3,那么水池中的水至少要多少小时才能排完?
6.实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)成正比例;1.5小时后(包括1.5小时)y与x成反比例.根据图中提供的信息,解答下列问题:
(1)写出一般成人喝半斤低度白酒后,y与x之间的函数关系式及相应的自变量取值范围;
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上21:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
7.初中老师在讲授某一次实验中,测得两个变量之间的关系如下表所示:
自变量x
1
2
3
4
12
因变量y
0.12
0.06
0.03
0.015
0.01
请你根据表格回答下列问题:
(1)这两个变量之间可能是怎样的函数关系?你是怎样作出判断的?请你简要说明理由;
(2)请你写出这个函数的解析式;
(3)表格中空缺的数值可能是多少?请你给出合理的数值.
8.某电厂有5000吨电煤.
(1)求:这些电煤能够使用的天数x(单位:天)与该厂平均每天用煤吨数y(单位:吨)之间的函数关系;
(2)若平均每天用煤200吨,则这批电煤能用多少天?
(3)若该电厂前10天每天用200吨,后因各地用电紧张,每天用电煤300吨,则这批电煤共可用多少天?
9.某市蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽植一种在自然光照且温度为18℃的条件下生长最快的新品种蔬菜,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(h)变化的函数图象.其中BC段是双曲线的一部分.根据图中信息解答下列问题:
(1)求BC段双曲线对应的函数表达式.
(2)当时间为16h时,大棚内的温度约为多少度?
10.如图,在平面直角坐标系xOy中,函数(x<0)的图象经过点A(﹣4,n),AB⊥x轴于B,点C与点A关于原点O对称,CD⊥x轴于D,△ABD的面积为8.
(1)求m、n的值.
(2)若直线y=kx+b(k≠0)经过点C,且与x轴、y轴分别交于点E、F.当CF=2CE时,求点F的坐标.
(3)将线段OA绕着点P(1,s)旋转180°,O、A的对应点分别是O1、A1.若O1、A1在同一双曲线上,则s=
.
参考答案
1.解:(1)由题意得:v==;
(2)当t=40时,v==2500,
2500﹣2000=500(m3),
答:实际平均每天至少需要比原计划增加500m3土方运输量.
2.解:(1)由题意得,S矩形ABCD=AD×DC=xy,
故y=.(5≤x)
(2)不能.当x=4时,y=15>12,不合题意;
(3)由y=,且x、y都是正整数,
可得x可取1,2,3,4,5,6,10,12,15,20,30,60,
∵2x+y≤26,0<y≤12,
∴符合条件的围建方案为:AD=5m,DC=12m或AD=6m,DC=10m或AD=10m,DC=6m.
3.解:(1)∵vt=280,且全程速度限定为不超过120千米/小时,
∴v关于t的函数表达式为:v=,(t≥).
(2)①8点至10点48分时间长为小时,8点至11点30分时间长为3.5小时
将t=3.5代入v=得v=80;将t=代入v=得v=100,
∴小汽车行驶速度v的范围为:80≤v≤100;
②强哥不能在当天10点前到达绿口机场.理由如下:
8点至10点前时间长为2小时,将t=2代入v=得v=140>120千米/小时,超速了.
故强哥不能在当天10点前到达绿口机场.
4.解:(1)设P=,将A(0.5,120)代入求出k=60,
∴P=;
(2)当P>150KPa时,气球将爆炸,
∴P≤150,即P=≤150,
解得V≥=0.4(m3).
故为了安全起见,气体的体积应不小于0.4(m3).
5.解:(1)设函数表达式为V=,把(6,3000)代入V=,
得3000=.
解得:k=18000,所以V与t之间的函数表达式为:V=;
(2)把t=2代入V=,得V=9000,
答:每小时的排水量应该是9
000
m3;
(3)把V=4
000代入V=,得t=4.5,
根据反比例函数的性质,V随t的增大而减小,因此水池中的水至少要4.5
h才能排完.
6.解:(1)由题意可得:当0≤x≤1.5时,设函数关系式为:y=kx,
则150=1.5k,
解得:k=100,
故y=100x,
当1.5≤x时,设函数关系式为:y=,
则a=150×1.5=225,
解得:a=225,
故y=(x≥1.5),
综上所述:y与x之间的两个函数关系式为:y=;
(2)第二天早上7:00不能驾车去上班.
理由:∵晚上21:00到第二天早上7:00,有10小时,
∴x=10时,y==22.5>20,
∴第二天早上7:00不能驾车去上班.
7.解:(1)由表中自变量x和因变量y的数值可知:
自变量x和因变量y的乘积都等于0.12,且随着自变量x值的逐渐增加,因变量y的值逐渐减少,故两个变量x和y之间可能是反比例函数关系.
(2)∵两自变量的乘积等于0.12,且两自变量为反比例函数关系,
∴y=;
(3)将x=3代入得:y=0.04;
将y=0.015代入得:x=8;
故答案为:8,0.04.
8.解:(1)由题意可得:y=;
(2)把x=200代入y=,
得y=25.
故这批电煤能用25天.
(3)前10天后还剩下5000﹣10×200=3000(吨)电煤,
可以用=10(天),故共可用20天.
9.解:(1)双曲线y=经过B(12,18),
∴18=,解得k=216.
∴故BC段的函数表达式为:y=;
(2)当x=16时,y==13.5.
答:当x=16时,大棚内的温度约为13.5度.
10.解:(1)∵A、C关于原点对称,
∴C(4,﹣n),
∵S△ABD=×8×(﹣n)=8,n=﹣2,
∴A(﹣4,﹣2),
∴m=8;
(2)由(1)得点C的坐标为C(4,2).
①如图1中,当k<0时,设直线y=kx+b与x轴,y轴的交点分别为点E1,F1.
由
CD⊥x轴于点D可得CD∥OF1.
∴△E1CD∽△E1F1O.
∴=,
∵CF1=2CE1,
∴=,
∴OF1=3DC=6,
∴点F1的坐标为F1(0,6).
②如图2,当k>0时,设直线y=kx+b与x轴,y轴的交点分别为点E2,F2.
同理可得CD∥OF2,=,
∵CF2=2CE2,
∴E2为线段CF2的中点,E2C=E2F2,
∴OF2=DC=2.
∴点F2的坐标为(0,﹣2).
综上所述,点F的坐标为(0,6)或(0,﹣2);
(3)∵将线段OA绕着点P(1,s)旋转180°,O、A的对应点分别是O1、A1.
∴O1(2,2s)、A1(6,2s+2),
∵O1、A1在同一双曲线上,
∴2×2s=6(2s+2),
解得:s=﹣.
故答案为:﹣.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
