5.6.2 函数y=Asin(ωx +φ)(一)-【新教材】人教A版(2019)高中数学必修第一册课件(42张PPT)
文档属性
| 名称 | 5.6.2 函数y=Asin(ωx +φ)(一)-【新教材】人教A版(2019)高中数学必修第一册课件(42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 10:00:46 | ||
图片预览










文档简介
第五章三角函数
§ 5.6.2函数y=Asin(ωx+φ)的图象(一)
探要点·究所然
情境导学
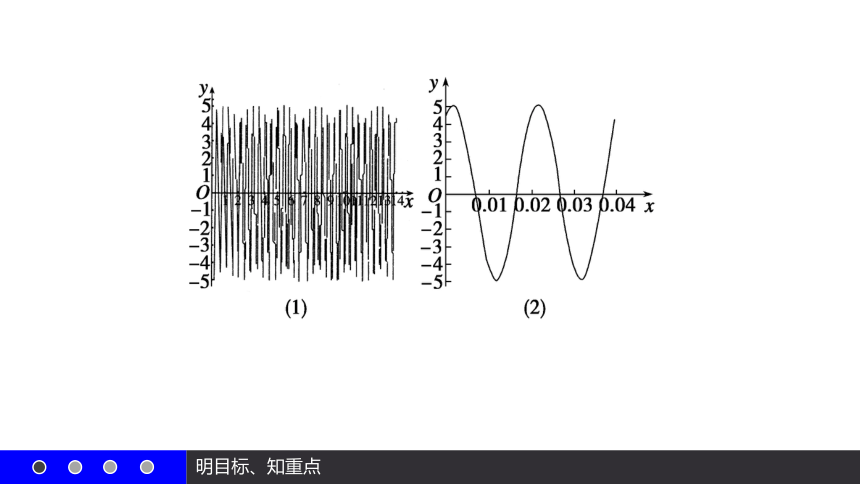
数学研究生活实际,那在某次实验里面,我们测得交流电电流y随着时间x变化的图象图(1),如果将图象局部放大,便得到图(2),看图(2)它跟我们上节课讲得正弦曲线非常相似,那这个图象,它是一个形如y=Asin(ωx+φ)的函数,那这个函数跟正弦函数究竟有什么关系呢?这就是这节课要研究的问题.
探究点一 φ对y=sin(x+φ),x∈R的图象的影响
答 列表如下:
0
π
2π
x
0
1
0
-1
0
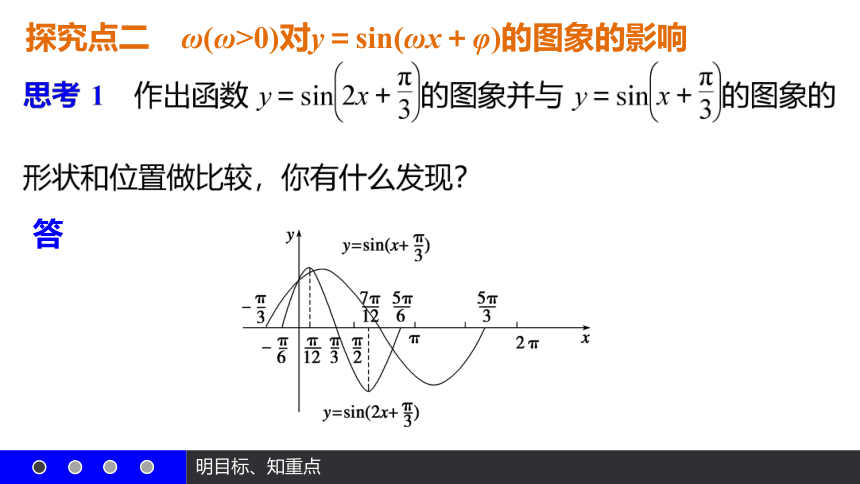
思考3 一般地,对任意的φ (φ≠0),函数y=sin(x+φ)的图象是由函数y=sin x的图象经过怎样的变换而得到的?
答 y=sin(x+φ)的图象,可以看作是把正弦曲线y=sin x上所有的点向左(当φ>0时)或向右(当φ<0时)平行移动|φ|个单位长度而得到,上述变换称为平移变换.
探究点二 ω(ω>0)对y=sin(ωx+φ)的图象的影响
答
答
?
探究点三 A(A>0)对y=Asin(ωx+φ)的图象的影响
答
思考3 一般地,对任意的A(A>0且A≠1),函数y=Asin(ωx+φ)的图象是由函数y=sin(ωx+φ)的图象经过怎样的变换而得到的?
答 函数y=Asin(ωx+φ)的图象,可以看作是把函数y=sin(ωx+φ)的图象上所有点的纵坐标伸长(当A>1时)或缩短(当0探究点四 函数y=Asin(ωx+φ)与y=sin x的图象关系
?
?
C
反思与感悟 已知两个函数的解析式,判断其图象间的平移关系的步骤:
①将两个函数解析式化简成y=Asin ωx与y=Asin(ωx+φ),即A、ω及名称相同的结构;
②找到ωx→ωx+φ,变量x“加”或“减”的量,即平移的单位为 ;
③明确平移的方向.
答案 A
答案 C
反思与感悟 三角函数图象变换容易出错,尤其是既涉及平移变换又涉及伸缩变换.平移时,若x的系数不是1,需把x的系数先提出,提出后括号中的x加或减的那个数才是平移的量,即x的净增量.方向的规律是“左加右减”.伸缩时,只改变x的系数ω,其余的量不变化,伸长时系数|ω|减小,缩短时|ω|增大.
答案 B
∴f(x)=3cos x.
反思与感悟 (1)本例已知变换途径及变换后的函数解析式,求变换前函数图象的解析式,宜采用逆变换的方法.
(2)已知函数f(x)图象的伸缩变换情况,求变换前后图象的解析式.要明确伸缩的方向及量,然后确定出A或ω即可.
C
当堂测·查疑缺
1
2
3
4
1
2
3
4
答案 A
1
2
3
4
C
1
2
3
4
1
2
3
4
y=-cos 2x
呈重点、现规律
1.由y=sin x的图象,通过变换可得到函数y=Asin(ωx+φ)(A>0,ω>0)的图象,其变化途径有两条:
§ 5.6.2函数y=Asin(ωx+φ)的图象(一)
探要点·究所然
情境导学
数学研究生活实际,那在某次实验里面,我们测得交流电电流y随着时间x变化的图象图(1),如果将图象局部放大,便得到图(2),看图(2)它跟我们上节课讲得正弦曲线非常相似,那这个图象,它是一个形如y=Asin(ωx+φ)的函数,那这个函数跟正弦函数究竟有什么关系呢?这就是这节课要研究的问题.
探究点一 φ对y=sin(x+φ),x∈R的图象的影响
答 列表如下:
0
π
2π
x
0
1
0
-1
0
思考3 一般地,对任意的φ (φ≠0),函数y=sin(x+φ)的图象是由函数y=sin x的图象经过怎样的变换而得到的?
答 y=sin(x+φ)的图象,可以看作是把正弦曲线y=sin x上所有的点向左(当φ>0时)或向右(当φ<0时)平行移动|φ|个单位长度而得到,上述变换称为平移变换.
探究点二 ω(ω>0)对y=sin(ωx+φ)的图象的影响
答
答
?
探究点三 A(A>0)对y=Asin(ωx+φ)的图象的影响
答
思考3 一般地,对任意的A(A>0且A≠1),函数y=Asin(ωx+φ)的图象是由函数y=sin(ωx+φ)的图象经过怎样的变换而得到的?
答 函数y=Asin(ωx+φ)的图象,可以看作是把函数y=sin(ωx+φ)的图象上所有点的纵坐标伸长(当A>1时)或缩短(当0
?
?
C
反思与感悟 已知两个函数的解析式,判断其图象间的平移关系的步骤:
①将两个函数解析式化简成y=Asin ωx与y=Asin(ωx+φ),即A、ω及名称相同的结构;
②找到ωx→ωx+φ,变量x“加”或“减”的量,即平移的单位为 ;
③明确平移的方向.
答案 A
答案 C
反思与感悟 三角函数图象变换容易出错,尤其是既涉及平移变换又涉及伸缩变换.平移时,若x的系数不是1,需把x的系数先提出,提出后括号中的x加或减的那个数才是平移的量,即x的净增量.方向的规律是“左加右减”.伸缩时,只改变x的系数ω,其余的量不变化,伸长时系数|ω|减小,缩短时|ω|增大.
答案 B
∴f(x)=3cos x.
反思与感悟 (1)本例已知变换途径及变换后的函数解析式,求变换前函数图象的解析式,宜采用逆变换的方法.
(2)已知函数f(x)图象的伸缩变换情况,求变换前后图象的解析式.要明确伸缩的方向及量,然后确定出A或ω即可.
C
当堂测·查疑缺
1
2
3
4
1
2
3
4
答案 A
1
2
3
4
C
1
2
3
4
1
2
3
4
y=-cos 2x
呈重点、现规律
1.由y=sin x的图象,通过变换可得到函数y=Asin(ωx+φ)(A>0,ω>0)的图象,其变化途径有两条:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
