人教A版高中数学必修3第一章1.1.2算法与程序框图课件(28张PPT)
文档属性
| 名称 | 人教A版高中数学必修3第一章1.1.2算法与程序框图课件(28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 479.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 10:05:39 | ||
图片预览




文档简介
1.1.2程序框图与算法的基本逻辑结构
-循环结构
温故知新
①顺序结构
是由若干个 的处理步骤组成的.
这是任何一个算法都离不
开的基本结构.
算法的基本逻辑结构
步骤 n
步骤n+1
示意图
依次执行
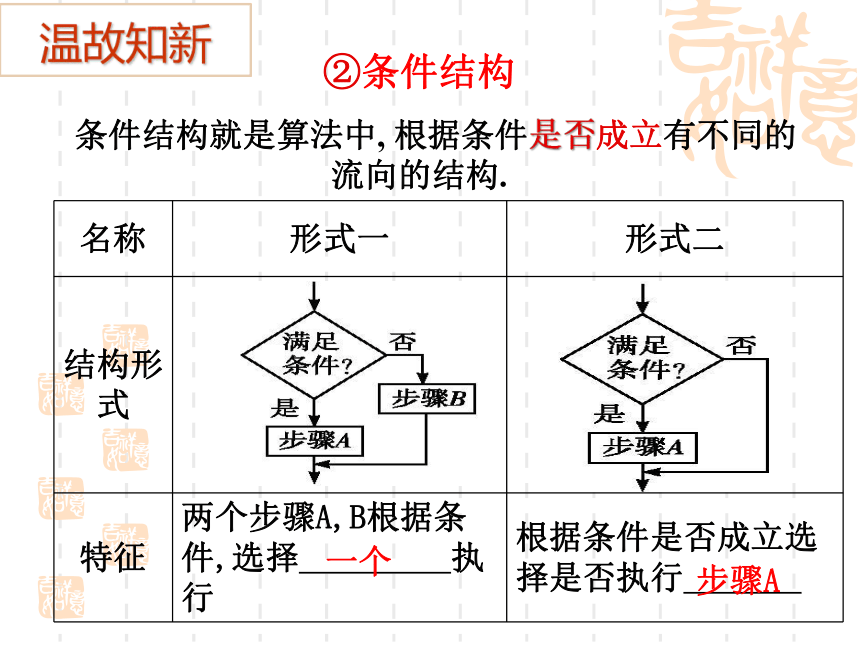
②条件结构
条件结构就是算法中, 根据条件是否成立有不同的流向的结构.
温故知新
名称
形式一
形式二
结构形式
特征
两个步骤A,B根据条件,选择 执行
根据条件是否成立选择是否执行 .
一个
步骤A
课前热身
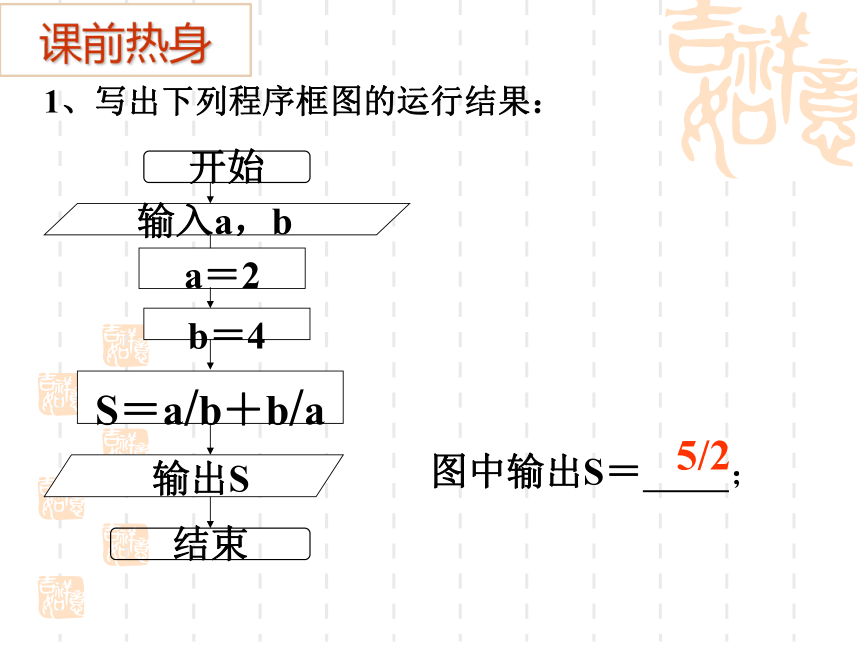
1、写出下列程序框图的运行结果:
开始
输入a,b
a=2
b=4
S=a/b+b/a
输出S
结束
图中输出S= ;
5/2
课前热身
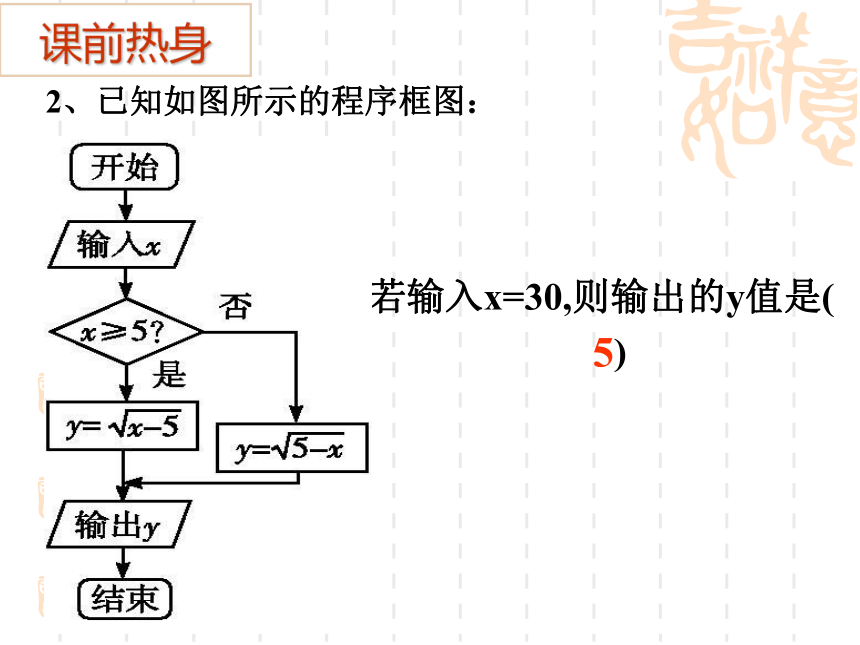
若输入x=30,则输出的y值是( )
2、已知如图所示的程序框图:
5
新课引入
例1设计算法求和:1+2+3+ … +100
这个算法中包含怎样的步骤呢?
思考1:
在一些算法中,经常会出现从某处开始,反复执行某一处理步骤,这就是循环结构.
包含重复执行的步骤
第1步,0+1=1.
第2步,1+2=3.
第3步,3+3=6.
第4步,6+4=10.
……
第100步,4950+100=5050
思考:计算1+2+3+…+100的值可按如下过程进行:
在一些算法中, 经常会出现从某处开始,按照一定的条件反复执行某些步骤的情况.这就是循环结构.反复执行的步骤称为循环体.
1.循环结构的概念
一、循环结构及框图表示
讲授新课
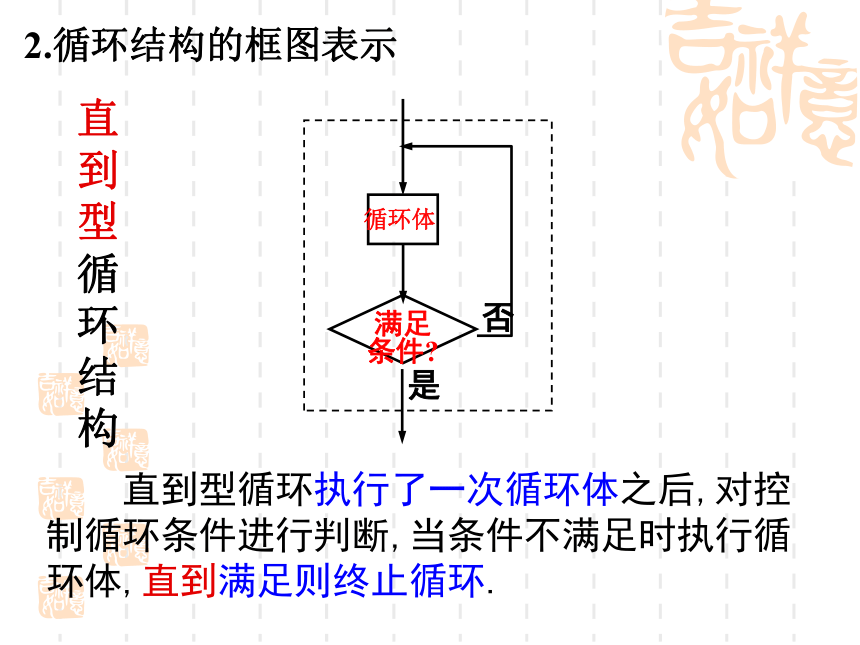
直到型循环执行了一次循环体之后,对控制循环条件进行判断,当条件不满足时执行循环体,直到满足则终止循环.
直到型循环结构
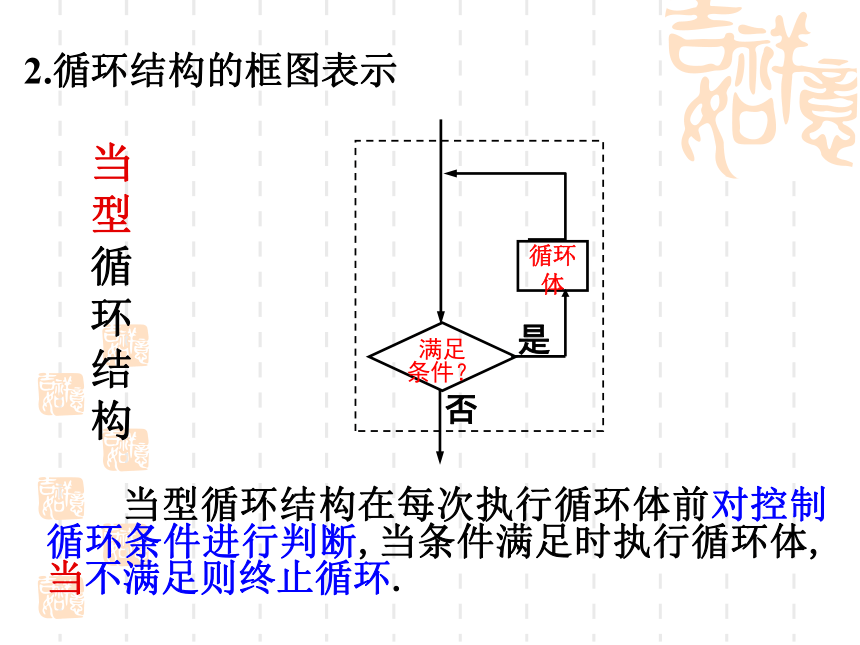
2.循环结构的框图表示
满足
条件?
是
否
循环体
当型循环结构
当型循环结构在每次执行循环体前对控制循环条件进行判断,当条件满足时执行循环体,当不满足则终止循环.
2.循环结构的框图表示
是
否
循环体
满足
条件?
名称
直到型循环结构
当型循环结构
结构
特征
先执行循环体,
后判断条件,
否循环
先判断条件,
后执行循环体,
是循环
3.循环结构的分类及特征
注意:循环结构不能是永无终止的“死循环”,
一定需要条件结构来确定何时终止执行循环体,因此,循环结构中一定包含条件结构.
牛刀小试
1.下列框图是循环结构的是( )
(A)①② (B)②③ (C)③④ (D)②④
C
直到型循环
当型循环
课堂实例
例1 设计一算法,求和:1+2+3+…+100
第1步,0+1=1.
第2步,1+2=3.
第3步,3+3=6.
第4步,6+4=10.
……
第100步,4950+100=5050.
我们发现这个算法中存在一些反复执行的步骤,于是我们尝试用循环结构表示。如何用循环结构表示出来呢?
课堂实例
第(i-1)步的结果+i=第i步的结果
思考2:各步骤有共同的结构:
为了方便有效地表示上述过程,我们引进一个累加变量S来表示每一步的计算结果,从而把第i步表示为:
S=0
S=S + 1
S=S + 2
S=S + 3
…
S=S + 100
例1 设计一算法,求和:1+2+3+…+100
S=S+i
引进一个计数变量i,依次取1,2,…,100,即把i+1仍记为i,即
第1步,0+1=1.
第2步,1+2=3.
第3步,3+3=6.
第4步,6+4=10.
……
第100步,4950+100=5050.
i=i+1
例1 设计一算法,求和:1+2+3+…+100
S=S+ i
i=i+1
3、怎么用程序框图表示呢?
4、S 有什么作用? i呢?
i = i + 1
S=S + i
S=0
S=S + 1
S=S + 2
S=S + 3
…
S=S + 100
累加变量S来表示每一步的计算结果, S的初始值为0
i的初始值为1,
i依次取1,2,…,100,
由于i同时记录了循环的次数,所以i称为计数变量.
循环体:
i = i + 1
S=S + i
解决方法就是加上一个判断,判断是否已经加到了100,如果加到了则退出,否则继续加。
直到型循环结构
当型循环结构
S = S + i
i=i+ 1
是
否
S= S+ i
i=i + 1
否
是
i≤100?
i>100?
请填上判断的条件。
5、如何设置循环终止条件?
试分析两种流程的异同点
算法(当型循环结构)
第一步:令i=1,s=0;
第二步:判断i ≤ 100是否
成立。若是,则执行第三步;
否则输出s,结束算法;
第三步:计算s=s+i;
第四步:计算i=i+1,
返回第二步
i=1
S=0
i≤100?
是
S=S+i
i=i+1
否
输出S
结束
当型循环结构
开始
例1 设计一算法,
求和:1+2+3+…+100
思考:如何用自然语言表述1.1-5中的直到型循环结构算法?
算法:
第一步:令i=1,s=0;
第二步:计算s=s+i;
第三步:计算i=i+1;
第四步:判断i >100是否
成立。若是,则输出s;
否则返回第二步。
结束
输出S
S= S+i
i= i+1
i>100?
否
是
S=0
i=1
开始
1.1-5
改进这一算法,表示输出1,1+2,1+2+3,…,1+2+3+…+(n-1)+n(n∈N※)的过程。
直到型循环结构
改进后的直到型循环结构程序图为:
结束
输出S
S= S+i
i= i+1
否
是
S=0
i=1
开始
输入n
i>n?
算法:
第一步:令i=1,s=0;
第二步:输入一个正整数n。
第三步:计算s=s+i;
第四步:计算i=i+1;
第五步:输出s
第六步:判断i >n是否成立。
若是,则结束算法;
否则返回第三步。
二、循环结构三要素 :
循环体、循环变量(初值)、循环终止条件
三、设计循环结构的三步曲:
(1)确定循环体
(2)初始化变量
(3)设置循环的终止条件.
课堂练习
1、设计一个计算 的值的算法,
并画出程序框图.
第一步:令i=1,s=1;
第三步:计算i=i+1;
第四步:判断i >50是否
成立。若是,则输出s;
否则返回第二步。
第二步:计算s=s×i;
算法步骤:
①确定循环体: S=____;i=i+1.
②初始化变量:
i=____,S=___.
③循环终止条件:
i___?
s×i
1
1
>50
课堂练习
1、设计一个计算 的值的算法,
并画出程序框图.
算法步骤:
第一步:令i=1,s=1;
第二步:计算s=s×i;
第三步:计算i=i+1;
第四步:判断i >50是否
成立。若是,则输出s;
否则返回第二步。
结束
输出S
S= S×i
i= i+1
否
是
S=1
i=1
开始
i>50?
课堂练习
2、程序框图如图所示.
变式1:右边的程序框图,若条件变为S>10?,
输出变为i=______?
变式2:若框图中先执行i=i+1 后执行 S=S+ i2,
则输出S=______?
输出S=______?
14
4
29
(A)i≤2 021? (B)i≤2 019?
(C)i≤2 017? (D)i≤2 015?
C
i>10?
课堂小结
1、循环结构:一定条件下反复执行
2. 循环结构的框图表示类型:直到型和当型
3、循环结构三要素 :
循环体、循环变量(初值)、循环终止条件
4、设计循环结构的三步曲:
(1)确定循环体
(2)初始化变量
(3)设置循环的终止条件.
课后作业
习题1.1 A组P2
谢谢!
-循环结构
温故知新
①顺序结构
是由若干个 的处理步骤组成的.
这是任何一个算法都离不
开的基本结构.
算法的基本逻辑结构
步骤 n
步骤n+1
示意图
依次执行
②条件结构
条件结构就是算法中, 根据条件是否成立有不同的流向的结构.
温故知新
名称
形式一
形式二
结构形式
特征
两个步骤A,B根据条件,选择 执行
根据条件是否成立选择是否执行 .
一个
步骤A
课前热身
1、写出下列程序框图的运行结果:
开始
输入a,b
a=2
b=4
S=a/b+b/a
输出S
结束
图中输出S= ;
5/2
课前热身
若输入x=30,则输出的y值是( )
2、已知如图所示的程序框图:
5
新课引入
例1设计算法求和:1+2+3+ … +100
这个算法中包含怎样的步骤呢?
思考1:
在一些算法中,经常会出现从某处开始,反复执行某一处理步骤,这就是循环结构.
包含重复执行的步骤
第1步,0+1=1.
第2步,1+2=3.
第3步,3+3=6.
第4步,6+4=10.
……
第100步,4950+100=5050
思考:计算1+2+3+…+100的值可按如下过程进行:
在一些算法中, 经常会出现从某处开始,按照一定的条件反复执行某些步骤的情况.这就是循环结构.反复执行的步骤称为循环体.
1.循环结构的概念
一、循环结构及框图表示
讲授新课
直到型循环执行了一次循环体之后,对控制循环条件进行判断,当条件不满足时执行循环体,直到满足则终止循环.
直到型循环结构
2.循环结构的框图表示
满足
条件?
是
否
循环体
当型循环结构
当型循环结构在每次执行循环体前对控制循环条件进行判断,当条件满足时执行循环体,当不满足则终止循环.
2.循环结构的框图表示
是
否
循环体
满足
条件?
名称
直到型循环结构
当型循环结构
结构
特征
先执行循环体,
后判断条件,
否循环
先判断条件,
后执行循环体,
是循环
3.循环结构的分类及特征
注意:循环结构不能是永无终止的“死循环”,
一定需要条件结构来确定何时终止执行循环体,因此,循环结构中一定包含条件结构.
牛刀小试
1.下列框图是循环结构的是( )
(A)①② (B)②③ (C)③④ (D)②④
C
直到型循环
当型循环
课堂实例
例1 设计一算法,求和:1+2+3+…+100
第1步,0+1=1.
第2步,1+2=3.
第3步,3+3=6.
第4步,6+4=10.
……
第100步,4950+100=5050.
我们发现这个算法中存在一些反复执行的步骤,于是我们尝试用循环结构表示。如何用循环结构表示出来呢?
课堂实例
第(i-1)步的结果+i=第i步的结果
思考2:各步骤有共同的结构:
为了方便有效地表示上述过程,我们引进一个累加变量S来表示每一步的计算结果,从而把第i步表示为:
S=0
S=S + 1
S=S + 2
S=S + 3
…
S=S + 100
例1 设计一算法,求和:1+2+3+…+100
S=S+i
引进一个计数变量i,依次取1,2,…,100,即把i+1仍记为i,即
第1步,0+1=1.
第2步,1+2=3.
第3步,3+3=6.
第4步,6+4=10.
……
第100步,4950+100=5050.
i=i+1
例1 设计一算法,求和:1+2+3+…+100
S=S+ i
i=i+1
3、怎么用程序框图表示呢?
4、S 有什么作用? i呢?
i = i + 1
S=S + i
S=0
S=S + 1
S=S + 2
S=S + 3
…
S=S + 100
累加变量S来表示每一步的计算结果, S的初始值为0
i的初始值为1,
i依次取1,2,…,100,
由于i同时记录了循环的次数,所以i称为计数变量.
循环体:
i = i + 1
S=S + i
解决方法就是加上一个判断,判断是否已经加到了100,如果加到了则退出,否则继续加。
直到型循环结构
当型循环结构
S = S + i
i=i+ 1
是
否
S= S+ i
i=i + 1
否
是
i≤100?
i>100?
请填上判断的条件。
5、如何设置循环终止条件?
试分析两种流程的异同点
算法(当型循环结构)
第一步:令i=1,s=0;
第二步:判断i ≤ 100是否
成立。若是,则执行第三步;
否则输出s,结束算法;
第三步:计算s=s+i;
第四步:计算i=i+1,
返回第二步
i=1
S=0
i≤100?
是
S=S+i
i=i+1
否
输出S
结束
当型循环结构
开始
例1 设计一算法,
求和:1+2+3+…+100
思考:如何用自然语言表述1.1-5中的直到型循环结构算法?
算法:
第一步:令i=1,s=0;
第二步:计算s=s+i;
第三步:计算i=i+1;
第四步:判断i >100是否
成立。若是,则输出s;
否则返回第二步。
结束
输出S
S= S+i
i= i+1
i>100?
否
是
S=0
i=1
开始
1.1-5
改进这一算法,表示输出1,1+2,1+2+3,…,1+2+3+…+(n-1)+n(n∈N※)的过程。
直到型循环结构
改进后的直到型循环结构程序图为:
结束
输出S
S= S+i
i= i+1
否
是
S=0
i=1
开始
输入n
i>n?
算法:
第一步:令i=1,s=0;
第二步:输入一个正整数n。
第三步:计算s=s+i;
第四步:计算i=i+1;
第五步:输出s
第六步:判断i >n是否成立。
若是,则结束算法;
否则返回第三步。
二、循环结构三要素 :
循环体、循环变量(初值)、循环终止条件
三、设计循环结构的三步曲:
(1)确定循环体
(2)初始化变量
(3)设置循环的终止条件.
课堂练习
1、设计一个计算 的值的算法,
并画出程序框图.
第一步:令i=1,s=1;
第三步:计算i=i+1;
第四步:判断i >50是否
成立。若是,则输出s;
否则返回第二步。
第二步:计算s=s×i;
算法步骤:
①确定循环体: S=____;i=i+1.
②初始化变量:
i=____,S=___.
③循环终止条件:
i___?
s×i
1
1
>50
课堂练习
1、设计一个计算 的值的算法,
并画出程序框图.
算法步骤:
第一步:令i=1,s=1;
第二步:计算s=s×i;
第三步:计算i=i+1;
第四步:判断i >50是否
成立。若是,则输出s;
否则返回第二步。
结束
输出S
S= S×i
i= i+1
否
是
S=1
i=1
开始
i>50?
课堂练习
2、程序框图如图所示.
变式1:右边的程序框图,若条件变为S>10?,
输出变为i=______?
变式2:若框图中先执行i=i+1 后执行 S=S+ i2,
则输出S=______?
输出S=______?
14
4
29
(A)i≤2 021? (B)i≤2 019?
(C)i≤2 017? (D)i≤2 015?
C
i>10?
课堂小结
1、循环结构:一定条件下反复执行
2. 循环结构的框图表示类型:直到型和当型
3、循环结构三要素 :
循环体、循环变量(初值)、循环终止条件
4、设计循环结构的三步曲:
(1)确定循环体
(2)初始化变量
(3)设置循环的终止条件.
课后作业
习题1.1 A组P2
谢谢!
