人教A版高中数学必修3第一章1.3 算法案例第一课时课件(28张PPT)
文档属性
| 名称 | 人教A版高中数学必修3第一章1.3 算法案例第一课时课件(28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 190.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 10:08:52 | ||
图片预览








文档简介
1.3 算法案例(第一课时)
高中数学必修3
表示算法的三种方式:
算法步骤(自然语言)
程序框图(图形语言)
计算机程序(程序语言)
一、复习引入
3 15
9 45
[问题1]:在小学,我们已经学过求最大公约数的知识,你能求出18与90的最大公约数吗?
18 30
2
3
∴18和90的最大公约数是2×3×3=18.
二、导入新课
1 5
3
介绍辗转相除法(欧几里得算法)
第一步 用两数中较大的数除以较小的数,求得商和余数
8251=6105×1+2146
第二步 对6105和2146重复第一步的做法
6105=2146×2+1813
同理6105和2146的最大公约数也是2146和1813的最大公约数。
为什么呢?
思考:从上述的过程你体会到了什么?
三、新课讲解
[问题2]:求8251与6105的最大公约数?
8251和6105的最大公约数为37
三、新课讲解
解:∵ 8251=6105×1+2146
6105=2146×2+1813
2146=1813×1+333
1813=333×5+148
333=148×2+37
148=37×4
例1.求8251与6105的最大公约数.
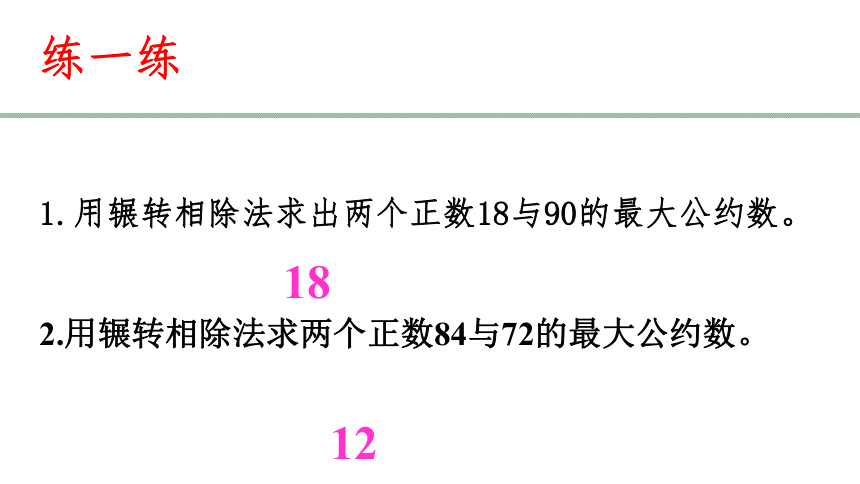
练一练
1.用辗转相除法求出两个正数18与90的最大公约数。
2.用辗转相除法求两个正数84与72的最大公约数。
18
12
分组探究(一)
分组探究问题:
1.辗转相除法定义
2.辗转相除法的算法步骤
3.辗转相除法的程序框图(直到型)
4.该程序框图的程序
5.当型循环结构的程序框图和程序
1.所谓辗转相除法定义
就是对于给定的两个数,用较大的数除以较小的数。若余数不为零,则将除数变被除数,余数变除数,继续上面的除法,直到大数被小数除尽,则这时最后的除数就是原来两个数的最大公约数。
辗转相除法是一个反复执行直到余数等于0停止的算法
四、归纳拓展
2.辗转相除法求最大公约数算法步骤
第一步,给定两个正数m,n
第二步,计算m除以n所得到余数r
第三步,m=n,n=r
第四步,若r=0,则m,n的最大公约数等于m;
否则,返回第二步
四、归纳拓展
INPUT m,n
DO
r=m MOD n
m=n
n=r
LOOP UNTIL r=0
PRINT m
END
开始
输入m,n
求m除以n的余数r
m=n
n=r
r=0?
是
输出m
结束
否
3辗转相除法的程序框图
4该程序框图的程序
四、归纳拓展
开始
输入m,n
求m除以n的余数r
m=n
n>0?
否
输出m
结束
是
n=r
INPUT m,n
WHILE n>0
r=m MODn
m=n
n=r
WEND
PRINT m
END
5.当型循环结构的程序框图和程序
问题3.介绍我国《九章算术》中的更相减损术
算理:可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之。
第一步:任意给定两个正整数;判断他们是否都是偶数。若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止,则这个等数就是所求的最大公约数。
新课讲解
例2用更相减损术求98与63的最大公约数.
解:由于63不是偶数,把98和63以大数减小数,并辗转相减,
即:98-63=35; 63-35=28;
35-28=7; 28-7=21;
21-7=14; 14-7=7.
所以,98与63的最大公约数是7。
新课讲解
练一练
1.用更项减损术求出两个正数18与90的最大公约数。
2.用更相减损术求两个正数84与72的最大公约数。
18
12
分组探究(二)
分组探究问题:
1.更相减损术定义
2.辗转相除法与更相减损术的比较
1.所谓更相减损术定义
就是对于给定的两个数,用较大的数减去较小的数,然后将差和较小的数构成新的一对数,再用较大的数减去较小的数,反复执行此步骤直到差数和较小的数相等,此时相等的两数便为原来两个数的最大公约数。
归纳拓展
2.辗转相除法与更相减损术的比较
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主;计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到.
归纳拓展
五、课堂测试
1.分别用辗转相除法和更相减损术求168与93的最大公约数.
2.求三个数175、100、75的最大公约数
1、分别用辗转相除法和更相减损术求168与93的最大公约数.
辗转相除法:168=93×1+75, 93=75×1+18, 75=18×4+3, 18=3×6.
更相减损术:168-93=75, 93-75=18,
75-18=57, 57-18=39,
39-18=21, 21-18=3,
18-3=15, 15-3=12,
12-3=9, 9-3=6,
6-3=3.
五、课堂测试
2、求三个数175、100、75的最大公约数.
分析:求三个数的最大公约数时,可以先求出其中两个数的最大公约数,用这个最大公约数再与第三个数求最大公约数,所得结果就是这三个数的最大公约数.
解:解法1(辗转相除法):先求175与100的最大公约数:175=100×1+75,100=75×1+25,
75=25×3. ∴175与100的最大公约数是25.
五、课堂测试
以下再求25与75的最大公约数:
75=25×3
∴25和75的最大公约数是25.
故25是75和25的最大公约数,也就是175、100、75的最大公约数.
五、课堂测试
解法2(更相减损术):
第一步:先从较大数中减去较小的数:
175-100=75,100-75=25,75-25=25;得25.第二步:重复上面的算法:75-25=50,50-25=25;得25.
∵25,25的最大公约数为25.
∴三个数175,100,75的最大公约数为25.
五、课堂测试
1.辗转相除法:就是对于给定的两个正整数,用较大的数除以较小的数,若余数不为零,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽为止,这时的较小的数即为原来两个数的最大公约数.
2. 更相减损术:就是对于给定的两个正整数,用较大的数减去较小的数,然后将差和较小的数构成新的一对数,继续上面的减法,直到差和较小的数相等,此时相等的两数即为原来两个数的最大公约数.
六、课堂小结
3、辗转相除法与更相减损术的区别
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到
六、课堂小结
1用辗转相除法计算60与48的最大公约数时,需要做的除法次数是( )
A.1 B.2
C.3 D.4
解析:∵60=48×1+12,48=12×4+0.
∴仅需要两步运算.
答案:B
七、巩固练习
2、下列各组关于最大公约数的说法中不正确的是( )
A.16和12的最大公约数是4
B.78和36的最大公约数是6
C.85和357的最大公约数是34
D.105和315的最大公约数是105
3、求378和90的最大公约数
(先用辗转相除法求,再用更相减损术验证)
解:∵378=90×4+18,90=18×5,
∴378和90的最大公约数是18.
七、巩固练习
答案:C
4:求三个数324,243,108的最大公约数.
解:先求324与243的最大公约数,
324=243×1+81,243=81×3,
∴324与243的最大公约数为81.
下面再求108与81的最大公约数:
108=81+27,81=27×3.
∴108与81的最大公约数是27.
故324,243,108的最大公约数为27.
七、巩固练习
八、布置作业
1.预习课本P37—39页及学案
2.书面作业
P45页练习1(1),(2),(3),(4)。
P48页习题1.3A组1(1),(2)。
3.根据更项减水率设计一个程序框图和程序
高中数学必修3
表示算法的三种方式:
算法步骤(自然语言)
程序框图(图形语言)
计算机程序(程序语言)
一、复习引入
3 15
9 45
[问题1]:在小学,我们已经学过求最大公约数的知识,你能求出18与90的最大公约数吗?
18 30
2
3
∴18和90的最大公约数是2×3×3=18.
二、导入新课
1 5
3
介绍辗转相除法(欧几里得算法)
第一步 用两数中较大的数除以较小的数,求得商和余数
8251=6105×1+2146
第二步 对6105和2146重复第一步的做法
6105=2146×2+1813
同理6105和2146的最大公约数也是2146和1813的最大公约数。
为什么呢?
思考:从上述的过程你体会到了什么?
三、新课讲解
[问题2]:求8251与6105的最大公约数?
8251和6105的最大公约数为37
三、新课讲解
解:∵ 8251=6105×1+2146
6105=2146×2+1813
2146=1813×1+333
1813=333×5+148
333=148×2+37
148=37×4
例1.求8251与6105的最大公约数.
练一练
1.用辗转相除法求出两个正数18与90的最大公约数。
2.用辗转相除法求两个正数84与72的最大公约数。
18
12
分组探究(一)
分组探究问题:
1.辗转相除法定义
2.辗转相除法的算法步骤
3.辗转相除法的程序框图(直到型)
4.该程序框图的程序
5.当型循环结构的程序框图和程序
1.所谓辗转相除法定义
就是对于给定的两个数,用较大的数除以较小的数。若余数不为零,则将除数变被除数,余数变除数,继续上面的除法,直到大数被小数除尽,则这时最后的除数就是原来两个数的最大公约数。
辗转相除法是一个反复执行直到余数等于0停止的算法
四、归纳拓展
2.辗转相除法求最大公约数算法步骤
第一步,给定两个正数m,n
第二步,计算m除以n所得到余数r
第三步,m=n,n=r
第四步,若r=0,则m,n的最大公约数等于m;
否则,返回第二步
四、归纳拓展
INPUT m,n
DO
r=m MOD n
m=n
n=r
LOOP UNTIL r=0
PRINT m
END
开始
输入m,n
求m除以n的余数r
m=n
n=r
r=0?
是
输出m
结束
否
3辗转相除法的程序框图
4该程序框图的程序
四、归纳拓展
开始
输入m,n
求m除以n的余数r
m=n
n>0?
否
输出m
结束
是
n=r
INPUT m,n
WHILE n>0
r=m MODn
m=n
n=r
WEND
PRINT m
END
5.当型循环结构的程序框图和程序
问题3.介绍我国《九章算术》中的更相减损术
算理:可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之。
第一步:任意给定两个正整数;判断他们是否都是偶数。若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止,则这个等数就是所求的最大公约数。
新课讲解
例2用更相减损术求98与63的最大公约数.
解:由于63不是偶数,把98和63以大数减小数,并辗转相减,
即:98-63=35; 63-35=28;
35-28=7; 28-7=21;
21-7=14; 14-7=7.
所以,98与63的最大公约数是7。
新课讲解
练一练
1.用更项减损术求出两个正数18与90的最大公约数。
2.用更相减损术求两个正数84与72的最大公约数。
18
12
分组探究(二)
分组探究问题:
1.更相减损术定义
2.辗转相除法与更相减损术的比较
1.所谓更相减损术定义
就是对于给定的两个数,用较大的数减去较小的数,然后将差和较小的数构成新的一对数,再用较大的数减去较小的数,反复执行此步骤直到差数和较小的数相等,此时相等的两数便为原来两个数的最大公约数。
归纳拓展
2.辗转相除法与更相减损术的比较
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主;计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到.
归纳拓展
五、课堂测试
1.分别用辗转相除法和更相减损术求168与93的最大公约数.
2.求三个数175、100、75的最大公约数
1、分别用辗转相除法和更相减损术求168与93的最大公约数.
辗转相除法:168=93×1+75, 93=75×1+18, 75=18×4+3, 18=3×6.
更相减损术:168-93=75, 93-75=18,
75-18=57, 57-18=39,
39-18=21, 21-18=3,
18-3=15, 15-3=12,
12-3=9, 9-3=6,
6-3=3.
五、课堂测试
2、求三个数175、100、75的最大公约数.
分析:求三个数的最大公约数时,可以先求出其中两个数的最大公约数,用这个最大公约数再与第三个数求最大公约数,所得结果就是这三个数的最大公约数.
解:解法1(辗转相除法):先求175与100的最大公约数:175=100×1+75,100=75×1+25,
75=25×3. ∴175与100的最大公约数是25.
五、课堂测试
以下再求25与75的最大公约数:
75=25×3
∴25和75的最大公约数是25.
故25是75和25的最大公约数,也就是175、100、75的最大公约数.
五、课堂测试
解法2(更相减损术):
第一步:先从较大数中减去较小的数:
175-100=75,100-75=25,75-25=25;得25.第二步:重复上面的算法:75-25=50,50-25=25;得25.
∵25,25的最大公约数为25.
∴三个数175,100,75的最大公约数为25.
五、课堂测试
1.辗转相除法:就是对于给定的两个正整数,用较大的数除以较小的数,若余数不为零,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽为止,这时的较小的数即为原来两个数的最大公约数.
2. 更相减损术:就是对于给定的两个正整数,用较大的数减去较小的数,然后将差和较小的数构成新的一对数,继续上面的减法,直到差和较小的数相等,此时相等的两数即为原来两个数的最大公约数.
六、课堂小结
3、辗转相除法与更相减损术的区别
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到
六、课堂小结
1用辗转相除法计算60与48的最大公约数时,需要做的除法次数是( )
A.1 B.2
C.3 D.4
解析:∵60=48×1+12,48=12×4+0.
∴仅需要两步运算.
答案:B
七、巩固练习
2、下列各组关于最大公约数的说法中不正确的是( )
A.16和12的最大公约数是4
B.78和36的最大公约数是6
C.85和357的最大公约数是34
D.105和315的最大公约数是105
3、求378和90的最大公约数
(先用辗转相除法求,再用更相减损术验证)
解:∵378=90×4+18,90=18×5,
∴378和90的最大公约数是18.
七、巩固练习
答案:C
4:求三个数324,243,108的最大公约数.
解:先求324与243的最大公约数,
324=243×1+81,243=81×3,
∴324与243的最大公约数为81.
下面再求108与81的最大公约数:
108=81+27,81=27×3.
∴108与81的最大公约数是27.
故324,243,108的最大公约数为27.
七、巩固练习
八、布置作业
1.预习课本P37—39页及学案
2.书面作业
P45页练习1(1),(2),(3),(4)。
P48页习题1.3A组1(1),(2)。
3.根据更项减水率设计一个程序框图和程序
