5.1.1相交线(共35张ppt)
图片预览











文档简介
(共35张PPT)
5.1
相交线
5.1.1
相交线
R·七年级下册
第五章
相交线与平行线
情景导入
观察这些图片,你能否看到相交线、平行线?
学习目标:
1.能说出相交线、邻补角、对顶角的意义以
及对顶角的性质.
2.能够灵活运用这几个意义和性质解决相关
问题.
这里有一把剪刀,握紧剪刀的把手,就能剪开物体,你能说出其中的道理吗?
探究新知
知识点1
邻补角
如果把剪子的构造抽象成一个几何图形,会是什么样的图形?请你在笔记本上画出.
仔细观察你所画的图形,当两条直线相交时,所形成的四个角中,∠1
与∠2
有怎样的位置关系?
∠1
与∠2
的顶点所在的位置有什么特点?
探究
A
B
C
D
O
1
2
3
4
仔细观察你所画的图形,当两条直线相交时,所形成的四个角中,∠1
与∠2
有怎样的位置关系?
∠1
与∠2
的边所在的位置有什么特点?
A
B
C
D
O
1
2
3
4
探究
图中还有哪些邻补角?
邻补角的定义:∠1
和∠2
有一条公共边OA,它们的另一边互为反向延长线(∠1
和∠2互补),具有这种关系的两个角,互为邻补角.
归纳
A
B
C
D
O
1
2
3
4
∠1
与∠3
有怎样的位置关系?
思考
知识点2
对顶角
A
B
C
D
O
1
2
3
4
图中还有哪些对顶角?
对顶角的定义:∠1
和∠3
有一个公共顶点
O,并且∠1
的两边分别是∠3
的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
A
B
C
D
O
1
2
3
4
归纳
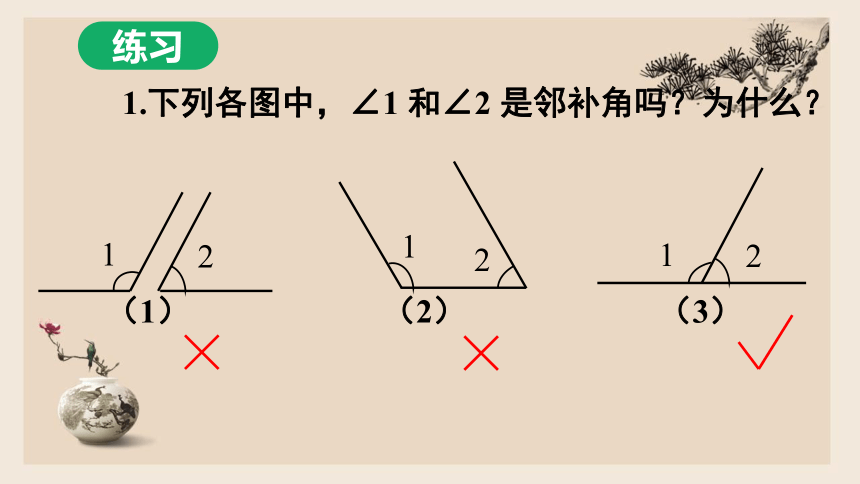
1.下列各图中,∠1
和∠2
是邻补角吗?为什么?
(1)
(2)
(3)
1
2
1
1
2
2
练习
2.下列各图中,∠1
和
∠2
是对顶角吗?为什么?
1
2
(2)
(3)
(4)
2
1
(1)
1
2
(5)
1
2
1
2
3.请分别画出图中∠1
的对顶角和
∠2
的邻补角.
2
1
4.如图,三条直线
AB
,CD
,EF
相交于点
O
,∠AOE
的对顶角是_______,∠EOD
的邻补角是__________________.
A
B
F
C
D
E
O
∠FOB
∠FOD、
∠COE
A
B
C
D
O
1
2
3
4
∠1
与∠2
有怎样的数量关系?
互
补
探究
∠1
与∠3
有怎样的数量关系?
你是怎样得到的?
A
B
C
D
O
1
2
3
4
相
等
你能说出∠1
=∠3
的道理吗?
因为
∠1
与∠2
互补,
∠3
与∠2
互补
(邻补角的定义),
所以
∠1
=∠3(同角的补角相等).
同理
∠2
=∠4
.
A
B
C
D
O
1
2
3
4
请你用数学的语言写出这个过程.
解:由邻补角定义,可得
∠2
=
180°-
∠1
=
180°-
40°
=
140°;
由对顶角相等,得
∠3
=
∠1
=
40°,∠4
=
∠2
=
140°.
例
如图,直线
a,b
相交,∠1
=
40°,求∠2
,∠3
,∠4
的度数.
1
2
3
4
a
b
1
2
3
4
a
b
例
如图,直线
a,b
相交,∠1
=
40°,求∠2
,∠3
,∠4
的度数.
变式训练
变式1
若∠1
+∠3
=
80°,
求各个角的度数.
∠1
=
∠
3
=
40°
∠1
+
∠3
=
2∠1
=
80°
∠2
=
∠
4
=
180°-
40?
=
140°
1
2
3
4
a
b
变式2
若∠2
是∠1
的
3.5
倍,
求各个角的度数.
∠1
+
∠2
=
∠1
+
3.5∠1
=
180°
∠1
=
∠
3
=
40°
变式3
若
?1
:?2
=
2
:7
,
求各个角的度数.
∠2
=
∠
4
=
180°-
40?
=
140°
取两根木条
a、b,将它们钉在一起,固定木条
a
,转动木条
b.
(1)当
a
与
b
所成锐角
α
为
35°时,其余的角分别为多少?
35°,
145°,
145°
练习
(2)当
a
与
b
所成角
α
为
90°
时,其余的角分别为多少?
均为90°
1.下列图形中,∠1
与∠2
是对顶角的是(
)
误区一
不能准确判断对顶角
错
解
正
解
A
或
C
或
D
B
错因分析
不理解互为对顶角的条件:(1)有公共顶点;(2)角的两边互为反向延长线.
A,C
或D
中的∠1
和∠2
不符合对顶角的条件.判断对顶角一定要抓住对顶角形成的前提条件是两直线相交.
2.判断:若∠1
+∠2
=
180°,则∠1
与∠2
是邻补角.
(
)
误区二
混淆邻补角和补角的概念
错
解
正
解
√
×
此题错在混淆补角和邻补角的概念.
邻补角必须满足的条件:(1)有一条公共边;(2)另一边互为反向延长线.
∠1
+∠2
=
180°,只能说明∠1与∠2互补,但互补的两个角不一定互为邻补角.
错因分析
基础巩固
随堂演练
1.
如图,直线
c
分别与直线
a、b
相交形成
8
个角,写出图中满足下列条件的角.
(1)∠1
的邻补角有_________;
(2)∠3
的邻补角有_________;
(3)∠5
的邻补角有_________;
(4)∠7
的邻补角有_________;
(5)对顶角有_____________________
_____________________.
∠2,∠4
∠6,∠8
∠1和∠3,∠2和∠4,∠5和∠7,∠6和∠8
∠2,∠4
∠6,∠8
2.如图,直线AB、CD
相交于点O,∠AOE=90°,如果∠1=20°,那么∠2=______,∠3=______,∠4=______.
20°
70°
160°
综合运用
3.如图,直线
AB,CD,EF
相交于点
O.
(1)写出∠AOC,∠BOE
的邻补角;
(2)写出∠DOA,∠EOC
的对顶角;
(3)如果∠AOC
=
50°,求∠BOD,∠COB的度数.
解:(1)∠AOC
的邻补角:∠BOC,∠AOD;
∠BOE
的邻补角:∠AOE,∠BOF;
(2)∠DOA
的对顶角是∠BOC;
∠EOC
的对顶角是∠DOF;
(3)因为∠BOD
是∠AOC
的对顶角,所以∠BOD
=∠AOC
=
50°;
因为∠COB
是∠AOC
的邻补角,所以
∠COB
=180°-∠AOC
=
130°.
课堂小结
相交线
邻补角
对顶角
互
补
相
等
定义
性质
定义
性质
A
B
C
D
O
1
2
3
4
如图,直线
AB,CD
相交于点
O,OA
平分∠EOC.
(1)若∠EOC
=
70°,求∠BOD
的度数;
(2)若∠EOC∶∠EOD
=
2∶3,求∠BOD
的度数.
解:(1)因为
OA
平分∠EOC
,所以∠AOC
=
∠EOC
=
35°,
又因为∠BOD
是∠AOC
的对顶角,所以∠BOD
=∠AOC
=
35°;
(2)因为∠EOC
是∠EOD
的邻补角,且∠EOC∶∠EOD
=
2∶3,所以∠EOC
=
72°,
所以∠AOC
=
∠EOC
=
36°,
所以∠BOD
=
∠AOC
=
36°.
1.
从课后习题中选取;
2.
完成练习册本课时的习题.
课后作业
5.1
相交线
5.1.1
相交线
R·七年级下册
第五章
相交线与平行线
情景导入
观察这些图片,你能否看到相交线、平行线?
学习目标:
1.能说出相交线、邻补角、对顶角的意义以
及对顶角的性质.
2.能够灵活运用这几个意义和性质解决相关
问题.
这里有一把剪刀,握紧剪刀的把手,就能剪开物体,你能说出其中的道理吗?
探究新知
知识点1
邻补角
如果把剪子的构造抽象成一个几何图形,会是什么样的图形?请你在笔记本上画出.
仔细观察你所画的图形,当两条直线相交时,所形成的四个角中,∠1
与∠2
有怎样的位置关系?
∠1
与∠2
的顶点所在的位置有什么特点?
探究
A
B
C
D
O
1
2
3
4
仔细观察你所画的图形,当两条直线相交时,所形成的四个角中,∠1
与∠2
有怎样的位置关系?
∠1
与∠2
的边所在的位置有什么特点?
A
B
C
D
O
1
2
3
4
探究
图中还有哪些邻补角?
邻补角的定义:∠1
和∠2
有一条公共边OA,它们的另一边互为反向延长线(∠1
和∠2互补),具有这种关系的两个角,互为邻补角.
归纳
A
B
C
D
O
1
2
3
4
∠1
与∠3
有怎样的位置关系?
思考
知识点2
对顶角
A
B
C
D
O
1
2
3
4
图中还有哪些对顶角?
对顶角的定义:∠1
和∠3
有一个公共顶点
O,并且∠1
的两边分别是∠3
的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
A
B
C
D
O
1
2
3
4
归纳
1.下列各图中,∠1
和∠2
是邻补角吗?为什么?
(1)
(2)
(3)
1
2
1
1
2
2
练习
2.下列各图中,∠1
和
∠2
是对顶角吗?为什么?
1
2
(2)
(3)
(4)
2
1
(1)
1
2
(5)
1
2
1
2
3.请分别画出图中∠1
的对顶角和
∠2
的邻补角.
2
1
4.如图,三条直线
AB
,CD
,EF
相交于点
O
,∠AOE
的对顶角是_______,∠EOD
的邻补角是__________________.
A
B
F
C
D
E
O
∠FOB
∠FOD、
∠COE
A
B
C
D
O
1
2
3
4
∠1
与∠2
有怎样的数量关系?
互
补
探究
∠1
与∠3
有怎样的数量关系?
你是怎样得到的?
A
B
C
D
O
1
2
3
4
相
等
你能说出∠1
=∠3
的道理吗?
因为
∠1
与∠2
互补,
∠3
与∠2
互补
(邻补角的定义),
所以
∠1
=∠3(同角的补角相等).
同理
∠2
=∠4
.
A
B
C
D
O
1
2
3
4
请你用数学的语言写出这个过程.
解:由邻补角定义,可得
∠2
=
180°-
∠1
=
180°-
40°
=
140°;
由对顶角相等,得
∠3
=
∠1
=
40°,∠4
=
∠2
=
140°.
例
如图,直线
a,b
相交,∠1
=
40°,求∠2
,∠3
,∠4
的度数.
1
2
3
4
a
b
1
2
3
4
a
b
例
如图,直线
a,b
相交,∠1
=
40°,求∠2
,∠3
,∠4
的度数.
变式训练
变式1
若∠1
+∠3
=
80°,
求各个角的度数.
∠1
=
∠
3
=
40°
∠1
+
∠3
=
2∠1
=
80°
∠2
=
∠
4
=
180°-
40?
=
140°
1
2
3
4
a
b
变式2
若∠2
是∠1
的
3.5
倍,
求各个角的度数.
∠1
+
∠2
=
∠1
+
3.5∠1
=
180°
∠1
=
∠
3
=
40°
变式3
若
?1
:?2
=
2
:7
,
求各个角的度数.
∠2
=
∠
4
=
180°-
40?
=
140°
取两根木条
a、b,将它们钉在一起,固定木条
a
,转动木条
b.
(1)当
a
与
b
所成锐角
α
为
35°时,其余的角分别为多少?
35°,
145°,
145°
练习
(2)当
a
与
b
所成角
α
为
90°
时,其余的角分别为多少?
均为90°
1.下列图形中,∠1
与∠2
是对顶角的是(
)
误区一
不能准确判断对顶角
错
解
正
解
A
或
C
或
D
B
错因分析
不理解互为对顶角的条件:(1)有公共顶点;(2)角的两边互为反向延长线.
A,C
或D
中的∠1
和∠2
不符合对顶角的条件.判断对顶角一定要抓住对顶角形成的前提条件是两直线相交.
2.判断:若∠1
+∠2
=
180°,则∠1
与∠2
是邻补角.
(
)
误区二
混淆邻补角和补角的概念
错
解
正
解
√
×
此题错在混淆补角和邻补角的概念.
邻补角必须满足的条件:(1)有一条公共边;(2)另一边互为反向延长线.
∠1
+∠2
=
180°,只能说明∠1与∠2互补,但互补的两个角不一定互为邻补角.
错因分析
基础巩固
随堂演练
1.
如图,直线
c
分别与直线
a、b
相交形成
8
个角,写出图中满足下列条件的角.
(1)∠1
的邻补角有_________;
(2)∠3
的邻补角有_________;
(3)∠5
的邻补角有_________;
(4)∠7
的邻补角有_________;
(5)对顶角有_____________________
_____________________.
∠2,∠4
∠6,∠8
∠1和∠3,∠2和∠4,∠5和∠7,∠6和∠8
∠2,∠4
∠6,∠8
2.如图,直线AB、CD
相交于点O,∠AOE=90°,如果∠1=20°,那么∠2=______,∠3=______,∠4=______.
20°
70°
160°
综合运用
3.如图,直线
AB,CD,EF
相交于点
O.
(1)写出∠AOC,∠BOE
的邻补角;
(2)写出∠DOA,∠EOC
的对顶角;
(3)如果∠AOC
=
50°,求∠BOD,∠COB的度数.
解:(1)∠AOC
的邻补角:∠BOC,∠AOD;
∠BOE
的邻补角:∠AOE,∠BOF;
(2)∠DOA
的对顶角是∠BOC;
∠EOC
的对顶角是∠DOF;
(3)因为∠BOD
是∠AOC
的对顶角,所以∠BOD
=∠AOC
=
50°;
因为∠COB
是∠AOC
的邻补角,所以
∠COB
=180°-∠AOC
=
130°.
课堂小结
相交线
邻补角
对顶角
互
补
相
等
定义
性质
定义
性质
A
B
C
D
O
1
2
3
4
如图,直线
AB,CD
相交于点
O,OA
平分∠EOC.
(1)若∠EOC
=
70°,求∠BOD
的度数;
(2)若∠EOC∶∠EOD
=
2∶3,求∠BOD
的度数.
解:(1)因为
OA
平分∠EOC
,所以∠AOC
=
∠EOC
=
35°,
又因为∠BOD
是∠AOC
的对顶角,所以∠BOD
=∠AOC
=
35°;
(2)因为∠EOC
是∠EOD
的邻补角,且∠EOC∶∠EOD
=
2∶3,所以∠EOC
=
72°,
所以∠AOC
=
∠EOC
=
36°,
所以∠BOD
=
∠AOC
=
36°.
1.
从课后习题中选取;
2.
完成练习册本课时的习题.
课后作业
