九年级下册数学第三章 圆单元基础拔高训练试卷(北师大版)(Word版 含答案)
文档属性
| 名称 | 九年级下册数学第三章 圆单元基础拔高训练试卷(北师大版)(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1013.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 11:00:46 | ||
图片预览


文档简介
九年级下册数学第三章 圆单元基础拔高训练试卷(北师大版)
一、单选题
1.下列说法中,正确的是( )
A.弦是直径 B.半圆是弧
C.过圆心的线段是直径 D.圆心相同半径相同的两个圆是同心圆
2.如图,在中,点在弦上移动,连接过点作交于点.若则的最大值是( )
A. B. C. D.
3.如图,是的直径,是的弦,且与交于点,连接.若则的度数是( )
A. B. C. D.
4.下列说法:(1)三点确定一个圆;(2)直径所对的圆周角是直角;(3)平分弦的直径垂直于弦,并且平分弦所对的弧;(4)相等的圆心角所对的弧相等;(5)圆内接四边形的对角互补.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
5.如图,是切线,为切点,是直径,,则( )
A. B. C. D.
6.如图,P为圆O外一点,分别切圆O于两点,若,则( ).
A.2 B.3 C.4 D.5
7.如图,四边形是的内接四边形,,则的度数为( )
A.70° B.90° C.100° D.110°
8.如图,点A,B,C在⊙O上,若,,则图中阴影部分的面积为( )
A. B. C. D.
9.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )
A.3cm B. cm C.2.5cm D. cm
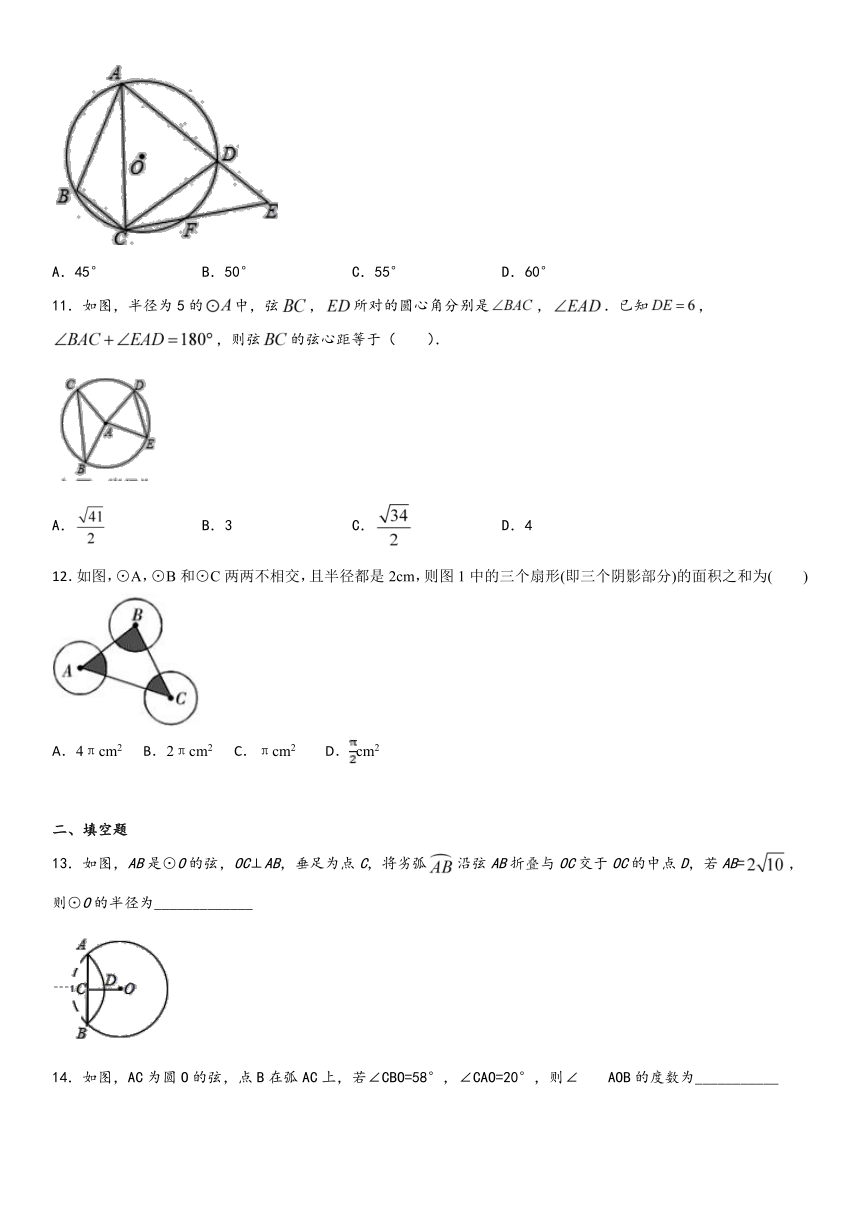
10.如图,四边形ABCD内接于⊙O,F是上一点,且,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A.45° B.50° C.55° D.60°
11.如图,半径为5的中,弦,所对的圆心角分别是,.已知,,则弦的弦心距等于( ).
A. B.3 C. D.4
12.如图,⊙A,⊙B和⊙C两两不相交,且半径都是2cm,则图1中的三个扇形(即三个阴影部分)的面积之和为( )
A.4πcm2 B.2πcm2 C.πcm2 D.cm2
二、填空题
13.如图,AB是⊙O的弦,OC⊥AB,垂足为点C,将劣弧沿弦AB折叠与OC交于OC的中点D,若AB=,则⊙O的半径为_____________
14.如图,AC为圆O的弦,点B在弧AC上,若∠CBO=58°,∠CAO=20°,则∠AOB的度数为___________
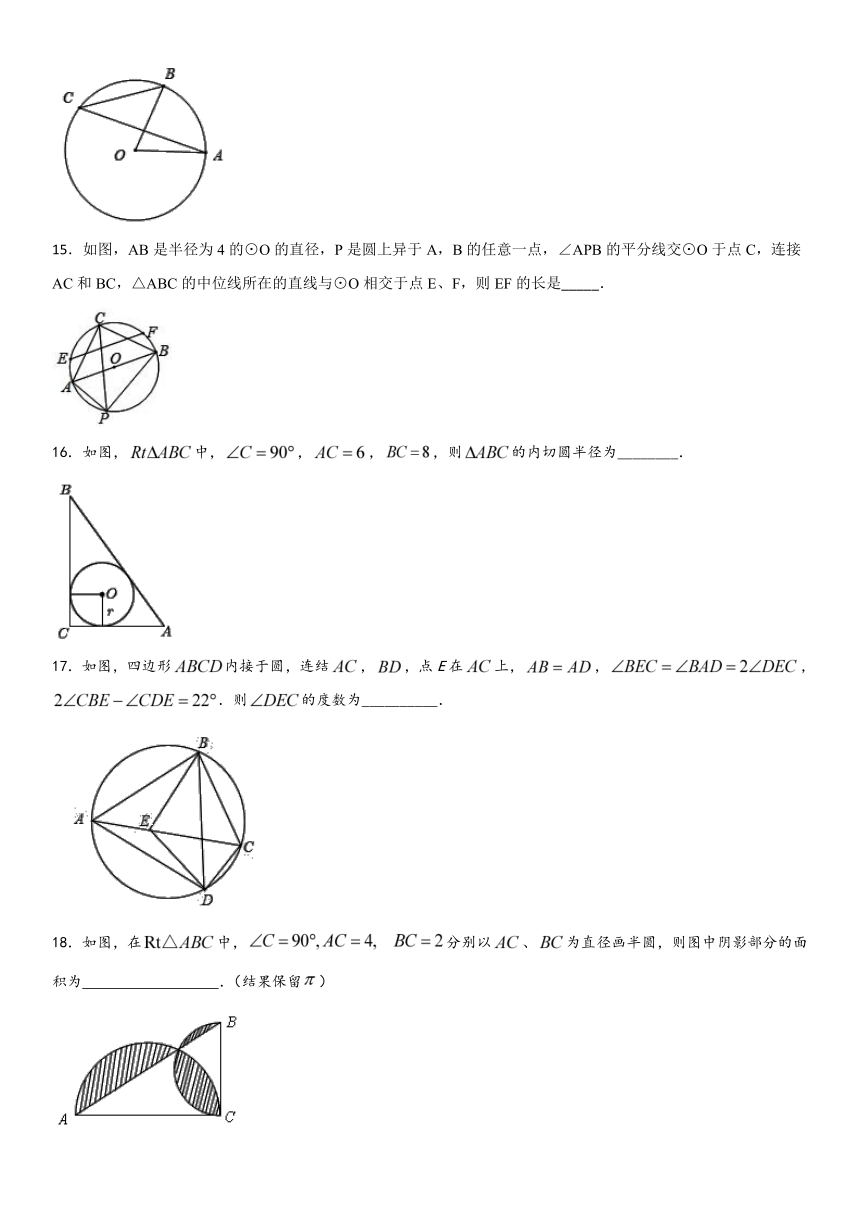
15.如图,AB是半径为4的⊙O的直径,P是圆上异于A,B的任意一点,∠APB的平分线交⊙O于点C,连接AC和BC,△ABC的中位线所在的直线与⊙O相交于点E、F,则EF的长是_____.
16.如图,中,,,,则的内切圆半径为________.
17.如图,四边形内接于圆,连结,,点E在上,,, .则的度数为__________.
18.如图,在中,分别以、为直径画半圆,则图中阴影部分的面积为 .(结果保留)
三、解答题
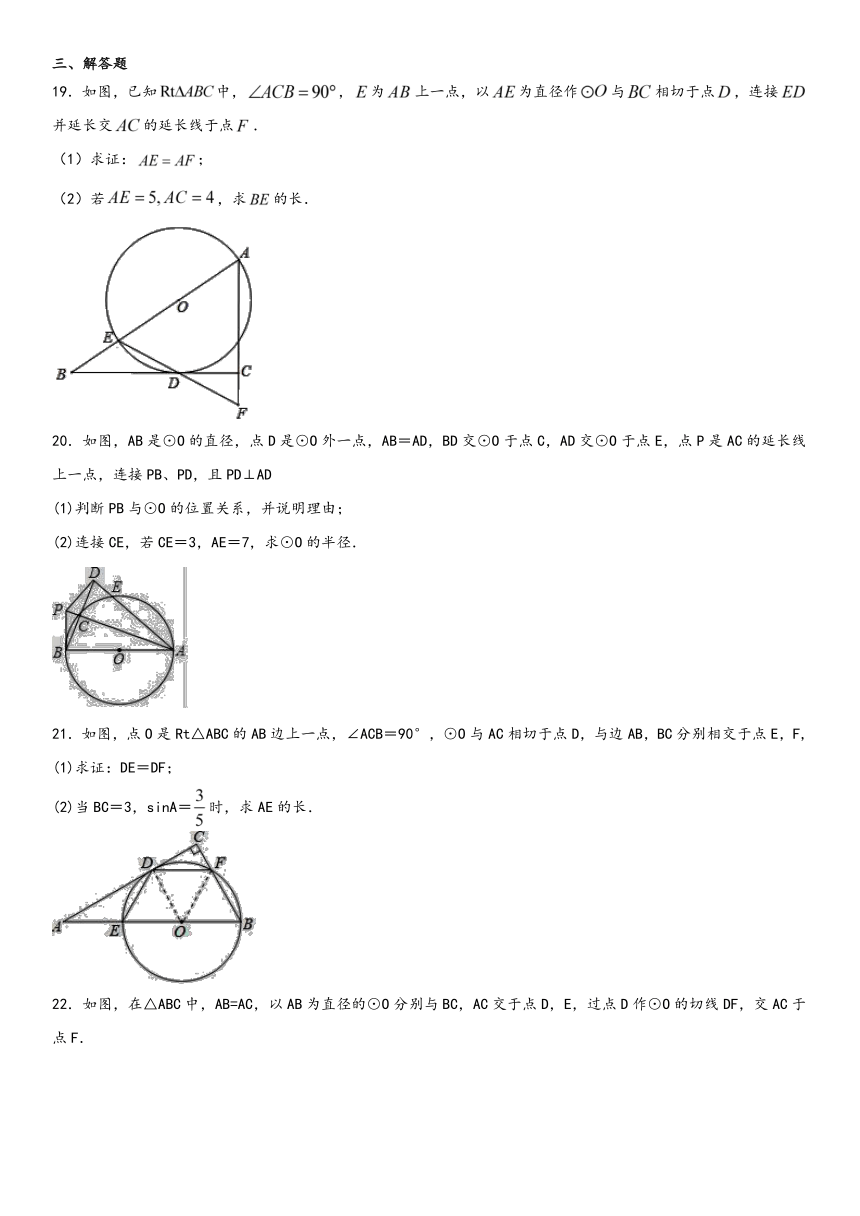
19.如图,已知中,,为上一点,以为直径作与相切于点,连接并延长交的延长线于点.
(1)求证:;
(2)若,求的长.
20.如图,AB是⊙O的直径,点D是⊙O外一点,AB=AD,BD交⊙O于点C,AD交⊙O于点E,点P是AC的延长线上一点,连接PB、PD,且PD⊥AD
(1)判断PB与⊙O的位置关系,并说明理由;
(2)连接CE,若CE=3,AE=7,求⊙O的半径.
21.如图,点O是Rt△ABC的AB边上一点,∠ACB=90°,⊙O与AC相切于点D,与边AB,BC分别相交于点E,F,
(1)求证:DE=DF;
(2)当BC=3,sinA=时,求AE的长.
22.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
23.如图,点 O 是△ABC 的边 AB 上一点,以 OB 为半径的⊙O 交 BC 于点 D,过点 D 的切线交 AC 于点 E,且 DE⊥AC.
(1)证明:AB=AC;
(2)设 AB=cm,BC=2cm,当点 O 在 AB 上移动到使⊙O 与边 AC 所在直线相切时, 求⊙O 的半径.
24.已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF,
(1)求证:AE是⊙O的直径;
(2)若∠ABC=∠EAC,AE=8,求AC的长.
25.如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若∠BEC=30°,求证:以BC,BE,AC边的三角形为直角三角形.
参考答案
1.B
试题:过圆心的弦是直径,不是所有的弦都是直径,故A选项错误;圆上任意两点间的部分是弧,故半圆是弧,故B正确;过圆心的弦是直径,故C选项错误;圆心相同,半径不等的两个圆是同心圆,故D错误,所以本题选B.
2.D
解:连接OD,如图,
∵CD⊥OC,
∴∠DCO=90?,
∴CD=,
当OC的值最小时,CD的值最大,
而OC⊥AB时,OC最小,此时D.?B两点重合,
∴CD=CB=AB=×2=1.
即CD的最大值为1.
故答案为:D.
.
3.B
如图:连接BD,
∵ ∠AOD=40°,
∴∠DOB=180°-40°=140°,
∴ ∠DCB=∠DOB=70°,
∵ CB=CD,
∴ ∠CBD=∠CDB=55°,
∵DO=BO,
∴∠ODB=∠OBD=20°,
∴∠CDO=∠CBO,
∴∠CDO=∠CDB-∠ODB=35°,
故选:B.
4.B
解:(1)任意三点确定一个圆;错误,应该是不在同一直线上的三点可以确定一个圆;
(2)直径所对的圆周角是直角;正确;
(3)平分弦的直径垂直于弦;并且平分弦所对的弧,错误,直径与直径互相平分,但不一定互相垂直;
(4)相等的圆心角所对的弧相等;错误,应该是在同圆或等圆中;
(5)圆内接四边形对角互补;正确;
5.C
解:连接OB,
∵PA、PB是⊙O切线,A、B为切点,
∴∠OAP=∠OBP=90°,
∵∠P=40°,
∴∠AOB=360°-∠OAP-∠P-∠OBP=140°,
∵OA=OB,
∴∠BAC=∠OBA=(180°-∠AOB)=20°,
故选:C.
6.D
∵P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=5,
∴PB=PA=5,
7.C
四边形是的内接四边形,,
,
8.C
..
9.D
解:连接OB,
∵AC是⊙O的直径,弦BD⊥AO于E,BD=8cm,AE=2cm.
在Rt△OEB中,OE2+BE2=OB2,即OE2+42=(OE+2)2
解得:OE=3,
∴OB=3+2=5,
∴EC=5+3=8.
在Rt△EBC中,BC=.
∵OF⊥BC,
∴∠OFC=∠CEB=90°.
∵∠C=∠C,
∴△OFC∽△BEC,
∴,即,
解得:OF=.
10.B
∵四边形ABCD内接于⊙O,∠ABC=105°,
∴∠ADC=180°﹣∠ABC=180°﹣105°=75°.
∵,∠BAC=25°,
∴∠DCE=∠BAC=25°,
∴∠E=∠ADC﹣∠DCE=75°﹣25°=50°.
B
解:作AH⊥BC于H,延长CA交于F ,连结BF,如下图
∵∠BAC+∠DAE=180°,∠BAC+∠BAF=180°,
∴∠DAE=∠BAF
∴DE= BF
∵
∴DE=BF=6
∵AH⊥BC
∴CH=BH
∵CA=AF
∴AH为的中位线
∴AH=BF=3
12.B
13.3.
解:连接OA,设半径为x,
∵将劣弧沿弦AB折叠交于OC的中点D,
∴OC=x,OC⊥AB,
∴AC=AB=,
∵OA2-OC2=AC2,
∴x2?(x)2=10,
解得,x=3.
故答案为:3.
14.76°
如图,连接OC.
∵OA=OC=OB,
∴∠A=∠OCA=20°,∠B=∠OCB=58°,
∴∠ACB=∠OCB?∠OCA=58°?20°=38°,
∴∠AOB=2∠ACB=76°,
故答案为76°.
15.4
16.
如图,
∵在,,,
∴由勾股定理得:,
∵圆O为的内切圆,
∴,;
四边形是正方形;
由切线长定理,得:,,;
,
即:,
故答案为:2.
17.34°
解:设∠
∴∠
∵四边形ABCD是圆的内接四边形
∴∠
即∠
又∵
∴∠,
∴∠
∴∠
∴∠
∵
∴
∴∠
∵∠,
∴∠
∴
∵
∴
∴,即
∴∠
∴∠
∴∠
18.
解: 设各个部分的面积为:S1、S2、S3、S4、S5,如图所示,
∵两个半圆的面积和是:S1+S5+S4+S2+S3+S4,△ABC的面积是S3+S4+S5,阴影部分的面积是:S1+S2+S4,
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积=π×4+π×1-4×2÷2=.
19.
(1)证明:连接,
∵切于点,
∴.
∴.
又,
∴,
∴.
∵,
∴,
∴.
∴.
(2)解:∵,
∴,
∴.
∵,
∴,
∴,
∴.
20.
(1)PB与⊙O相切,理由如下:
∵AB是⊙O的直径,
∴AC⊥BD,
又AB=AD,
∴AP是线段BD的垂直平分线,
∴PB=PD,
在△ABP和△ADP中,
,
∴△ABP≌△ADP(SSS),
∴∠ABP=∠ADP=90°,
∴PB与⊙O相切;
(2)∵△ABP≌△ADP,
∴∠BAC=∠DAC,
∴,
∴BC=CE=3,
∵AB=AD,AC⊥BD,
∴BC=CD=3,
∵四边形ABCE是⊙O的内接四边形,
∴∠DBA+∠CEA=180°,
∵∠DEC+∠CEA=180°,
∴∠DBA=∠DEC,
又∵∠CDE=∠ADB,
∴△DCE∽△DAB,
∴DC:DA=DE:DB,
∴DC?DB=DE?DA,即3×6=DE×(DE+7),
解得,DE=2,
∴DA=2+7=9,
∴AB=AD=9,
∴⊙O的半径为4.5.
21.
解:(1)如图所示,连接OD,OF,
∵⊙O与AC相切于点D,
∴∠ADO=90°,
∵∠ACB=90°,
∴OD∥BC,
∴∠AOD=∠ABC,∠DOF=∠OFB,
∵OB=OF,
∴∠ABC=∠OFB,
∴∠AOD=∠DOF,
∴DE=DF;
(2)在Rt△ABC中,∵BC=3,sinA==,
∴AB=5,
设⊙O的半径为r,则OB=OD=OE=r,
则AO=AB﹣OB=5﹣r,AE=5﹣2r,
在Rt△AOD中,∵sinA==,
∴=,解得r=,
则AE=5﹣2r=.
22.
(1)证明:连接,
,
,
∵AB=AC,
∴∠ABC=∠ACB.
∴∠ODB=∠ACB,
∴OD∥AC.
∵DF是⊙O的切线,
∴DF⊥OD.
∴DF⊥AC.
(2)连结OE,
∵DF⊥AC,∠CDF=22.5°.
∴∠ABC=∠ACB=67.5°,∴∠BAC=45°.
∵OA=OE,∴∠AOE=90°.
的半径为4,
,,
.
23.
(1)连接OD,
∵DE是⊙O的切线,
∵DE⊥OD,
∵AC⊥DE,
∴OD∥AC,
∴∠ODB=∠C,
∵OB=OD,
∴∠B=∠ODB,
∴∠B=∠C,
∴AB=AC;
(2)设AC与⊙O相切于点F,连接OF,作AH⊥BC于H,设半径为r,
∵AB=AC,AH⊥BC,
∴BH=CH=1,
∴AH==2,
∴tan∠C==2,
∵∠OFE=∠ODE=∠DEF=90°,
∴四边形ODEF是矩形,
∵OD=OF,
∴四边形ODEF是正方形,
∴EF=DE=r,
∵tanC==2,
∴EC=,
∴AF=﹣r﹣r=﹣r,
在Rt△AOF中,∵OA2=AF2+OF2,
∴(﹣r)2=r2+(﹣r)2,
解得r=.
24.
(1)证明:∵BE=CF,
∴弧BE=弧CF,
∴∠BAE=∠CAF,
∵AF⊥BC,
∴ADC=90°,
∴∠FAC+∠ACD=90°,
∵∠E=∠ACB,
∴∠E+∠BAE=90°,
∴∠ABE=90°,
∴AE是⊙O的直径;
(2)如图,连接OC,
∴∠AOC=2∠ABC,
∵∠ABC=∠CAE,
∴∠AOC=2∠CAE,
∵OA=OC,
∴∠CAO=∠ACO=∠AOC,
∴△AOC是等腰直角三角形,
∵AE=8,
∴AO=CO=4,
∴AC=4.
25.
解:证明:(1)如图1,连接OC,
∵DP是O的切线,
∴OC⊥DP,
又∵AD⊥DP,
∴OC∥AD,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
即AC平分∠DAB;
(2)∵PD是O的切线,
∴∠BCP=∠CAB,
又∵CE平分∠ACB,
∴∠ACF=∠BCF,
∴∠CAF+∠ACF=∠BCF+∠PCB,
即∠CFP=∠PCF,
∴PC=PF,即△PCB为等腰三角形;
(2)如图2,连接AE,
∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴AE=BE,
又∵AB为直径,
∴
∵
∴
∴在Rt△ABC中,
∴
∴以BC,BE,AC边的三角形为直角三角形.
一、单选题
1.下列说法中,正确的是( )
A.弦是直径 B.半圆是弧
C.过圆心的线段是直径 D.圆心相同半径相同的两个圆是同心圆
2.如图,在中,点在弦上移动,连接过点作交于点.若则的最大值是( )
A. B. C. D.
3.如图,是的直径,是的弦,且与交于点,连接.若则的度数是( )
A. B. C. D.
4.下列说法:(1)三点确定一个圆;(2)直径所对的圆周角是直角;(3)平分弦的直径垂直于弦,并且平分弦所对的弧;(4)相等的圆心角所对的弧相等;(5)圆内接四边形的对角互补.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
5.如图,是切线,为切点,是直径,,则( )
A. B. C. D.
6.如图,P为圆O外一点,分别切圆O于两点,若,则( ).
A.2 B.3 C.4 D.5
7.如图,四边形是的内接四边形,,则的度数为( )
A.70° B.90° C.100° D.110°
8.如图,点A,B,C在⊙O上,若,,则图中阴影部分的面积为( )
A. B. C. D.
9.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )
A.3cm B. cm C.2.5cm D. cm
10.如图,四边形ABCD内接于⊙O,F是上一点,且,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A.45° B.50° C.55° D.60°
11.如图,半径为5的中,弦,所对的圆心角分别是,.已知,,则弦的弦心距等于( ).
A. B.3 C. D.4
12.如图,⊙A,⊙B和⊙C两两不相交,且半径都是2cm,则图1中的三个扇形(即三个阴影部分)的面积之和为( )
A.4πcm2 B.2πcm2 C.πcm2 D.cm2
二、填空题
13.如图,AB是⊙O的弦,OC⊥AB,垂足为点C,将劣弧沿弦AB折叠与OC交于OC的中点D,若AB=,则⊙O的半径为_____________
14.如图,AC为圆O的弦,点B在弧AC上,若∠CBO=58°,∠CAO=20°,则∠AOB的度数为___________
15.如图,AB是半径为4的⊙O的直径,P是圆上异于A,B的任意一点,∠APB的平分线交⊙O于点C,连接AC和BC,△ABC的中位线所在的直线与⊙O相交于点E、F,则EF的长是_____.
16.如图,中,,,,则的内切圆半径为________.
17.如图,四边形内接于圆,连结,,点E在上,,, .则的度数为__________.
18.如图,在中,分别以、为直径画半圆,则图中阴影部分的面积为 .(结果保留)
三、解答题
19.如图,已知中,,为上一点,以为直径作与相切于点,连接并延长交的延长线于点.
(1)求证:;
(2)若,求的长.
20.如图,AB是⊙O的直径,点D是⊙O外一点,AB=AD,BD交⊙O于点C,AD交⊙O于点E,点P是AC的延长线上一点,连接PB、PD,且PD⊥AD
(1)判断PB与⊙O的位置关系,并说明理由;
(2)连接CE,若CE=3,AE=7,求⊙O的半径.
21.如图,点O是Rt△ABC的AB边上一点,∠ACB=90°,⊙O与AC相切于点D,与边AB,BC分别相交于点E,F,
(1)求证:DE=DF;
(2)当BC=3,sinA=时,求AE的长.
22.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
23.如图,点 O 是△ABC 的边 AB 上一点,以 OB 为半径的⊙O 交 BC 于点 D,过点 D 的切线交 AC 于点 E,且 DE⊥AC.
(1)证明:AB=AC;
(2)设 AB=cm,BC=2cm,当点 O 在 AB 上移动到使⊙O 与边 AC 所在直线相切时, 求⊙O 的半径.
24.已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF,
(1)求证:AE是⊙O的直径;
(2)若∠ABC=∠EAC,AE=8,求AC的长.
25.如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若∠BEC=30°,求证:以BC,BE,AC边的三角形为直角三角形.
参考答案
1.B
试题:过圆心的弦是直径,不是所有的弦都是直径,故A选项错误;圆上任意两点间的部分是弧,故半圆是弧,故B正确;过圆心的弦是直径,故C选项错误;圆心相同,半径不等的两个圆是同心圆,故D错误,所以本题选B.
2.D
解:连接OD,如图,
∵CD⊥OC,
∴∠DCO=90?,
∴CD=,
当OC的值最小时,CD的值最大,
而OC⊥AB时,OC最小,此时D.?B两点重合,
∴CD=CB=AB=×2=1.
即CD的最大值为1.
故答案为:D.
.
3.B
如图:连接BD,
∵ ∠AOD=40°,
∴∠DOB=180°-40°=140°,
∴ ∠DCB=∠DOB=70°,
∵ CB=CD,
∴ ∠CBD=∠CDB=55°,
∵DO=BO,
∴∠ODB=∠OBD=20°,
∴∠CDO=∠CBO,
∴∠CDO=∠CDB-∠ODB=35°,
故选:B.
4.B
解:(1)任意三点确定一个圆;错误,应该是不在同一直线上的三点可以确定一个圆;
(2)直径所对的圆周角是直角;正确;
(3)平分弦的直径垂直于弦;并且平分弦所对的弧,错误,直径与直径互相平分,但不一定互相垂直;
(4)相等的圆心角所对的弧相等;错误,应该是在同圆或等圆中;
(5)圆内接四边形对角互补;正确;
5.C
解:连接OB,
∵PA、PB是⊙O切线,A、B为切点,
∴∠OAP=∠OBP=90°,
∵∠P=40°,
∴∠AOB=360°-∠OAP-∠P-∠OBP=140°,
∵OA=OB,
∴∠BAC=∠OBA=(180°-∠AOB)=20°,
故选:C.
6.D
∵P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=5,
∴PB=PA=5,
7.C
四边形是的内接四边形,,
,
8.C
..
9.D
解:连接OB,
∵AC是⊙O的直径,弦BD⊥AO于E,BD=8cm,AE=2cm.
在Rt△OEB中,OE2+BE2=OB2,即OE2+42=(OE+2)2
解得:OE=3,
∴OB=3+2=5,
∴EC=5+3=8.
在Rt△EBC中,BC=.
∵OF⊥BC,
∴∠OFC=∠CEB=90°.
∵∠C=∠C,
∴△OFC∽△BEC,
∴,即,
解得:OF=.
10.B
∵四边形ABCD内接于⊙O,∠ABC=105°,
∴∠ADC=180°﹣∠ABC=180°﹣105°=75°.
∵,∠BAC=25°,
∴∠DCE=∠BAC=25°,
∴∠E=∠ADC﹣∠DCE=75°﹣25°=50°.
B
解:作AH⊥BC于H,延长CA交于F ,连结BF,如下图
∵∠BAC+∠DAE=180°,∠BAC+∠BAF=180°,
∴∠DAE=∠BAF
∴DE= BF
∵
∴DE=BF=6
∵AH⊥BC
∴CH=BH
∵CA=AF
∴AH为的中位线
∴AH=BF=3
12.B
13.3.
解:连接OA,设半径为x,
∵将劣弧沿弦AB折叠交于OC的中点D,
∴OC=x,OC⊥AB,
∴AC=AB=,
∵OA2-OC2=AC2,
∴x2?(x)2=10,
解得,x=3.
故答案为:3.
14.76°
如图,连接OC.
∵OA=OC=OB,
∴∠A=∠OCA=20°,∠B=∠OCB=58°,
∴∠ACB=∠OCB?∠OCA=58°?20°=38°,
∴∠AOB=2∠ACB=76°,
故答案为76°.
15.4
16.
如图,
∵在,,,
∴由勾股定理得:,
∵圆O为的内切圆,
∴,;
四边形是正方形;
由切线长定理,得:,,;
,
即:,
故答案为:2.
17.34°
解:设∠
∴∠
∵四边形ABCD是圆的内接四边形
∴∠
即∠
又∵
∴∠,
∴∠
∴∠
∴∠
∵
∴
∴∠
∵∠,
∴∠
∴
∵
∴
∴,即
∴∠
∴∠
∴∠
18.
解: 设各个部分的面积为:S1、S2、S3、S4、S5,如图所示,
∵两个半圆的面积和是:S1+S5+S4+S2+S3+S4,△ABC的面积是S3+S4+S5,阴影部分的面积是:S1+S2+S4,
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积=π×4+π×1-4×2÷2=.
19.
(1)证明:连接,
∵切于点,
∴.
∴.
又,
∴,
∴.
∵,
∴,
∴.
∴.
(2)解:∵,
∴,
∴.
∵,
∴,
∴,
∴.
20.
(1)PB与⊙O相切,理由如下:
∵AB是⊙O的直径,
∴AC⊥BD,
又AB=AD,
∴AP是线段BD的垂直平分线,
∴PB=PD,
在△ABP和△ADP中,
,
∴△ABP≌△ADP(SSS),
∴∠ABP=∠ADP=90°,
∴PB与⊙O相切;
(2)∵△ABP≌△ADP,
∴∠BAC=∠DAC,
∴,
∴BC=CE=3,
∵AB=AD,AC⊥BD,
∴BC=CD=3,
∵四边形ABCE是⊙O的内接四边形,
∴∠DBA+∠CEA=180°,
∵∠DEC+∠CEA=180°,
∴∠DBA=∠DEC,
又∵∠CDE=∠ADB,
∴△DCE∽△DAB,
∴DC:DA=DE:DB,
∴DC?DB=DE?DA,即3×6=DE×(DE+7),
解得,DE=2,
∴DA=2+7=9,
∴AB=AD=9,
∴⊙O的半径为4.5.
21.
解:(1)如图所示,连接OD,OF,
∵⊙O与AC相切于点D,
∴∠ADO=90°,
∵∠ACB=90°,
∴OD∥BC,
∴∠AOD=∠ABC,∠DOF=∠OFB,
∵OB=OF,
∴∠ABC=∠OFB,
∴∠AOD=∠DOF,
∴DE=DF;
(2)在Rt△ABC中,∵BC=3,sinA==,
∴AB=5,
设⊙O的半径为r,则OB=OD=OE=r,
则AO=AB﹣OB=5﹣r,AE=5﹣2r,
在Rt△AOD中,∵sinA==,
∴=,解得r=,
则AE=5﹣2r=.
22.
(1)证明:连接,
,
,
∵AB=AC,
∴∠ABC=∠ACB.
∴∠ODB=∠ACB,
∴OD∥AC.
∵DF是⊙O的切线,
∴DF⊥OD.
∴DF⊥AC.
(2)连结OE,
∵DF⊥AC,∠CDF=22.5°.
∴∠ABC=∠ACB=67.5°,∴∠BAC=45°.
∵OA=OE,∴∠AOE=90°.
的半径为4,
,,
.
23.
(1)连接OD,
∵DE是⊙O的切线,
∵DE⊥OD,
∵AC⊥DE,
∴OD∥AC,
∴∠ODB=∠C,
∵OB=OD,
∴∠B=∠ODB,
∴∠B=∠C,
∴AB=AC;
(2)设AC与⊙O相切于点F,连接OF,作AH⊥BC于H,设半径为r,
∵AB=AC,AH⊥BC,
∴BH=CH=1,
∴AH==2,
∴tan∠C==2,
∵∠OFE=∠ODE=∠DEF=90°,
∴四边形ODEF是矩形,
∵OD=OF,
∴四边形ODEF是正方形,
∴EF=DE=r,
∵tanC==2,
∴EC=,
∴AF=﹣r﹣r=﹣r,
在Rt△AOF中,∵OA2=AF2+OF2,
∴(﹣r)2=r2+(﹣r)2,
解得r=.
24.
(1)证明:∵BE=CF,
∴弧BE=弧CF,
∴∠BAE=∠CAF,
∵AF⊥BC,
∴ADC=90°,
∴∠FAC+∠ACD=90°,
∵∠E=∠ACB,
∴∠E+∠BAE=90°,
∴∠ABE=90°,
∴AE是⊙O的直径;
(2)如图,连接OC,
∴∠AOC=2∠ABC,
∵∠ABC=∠CAE,
∴∠AOC=2∠CAE,
∵OA=OC,
∴∠CAO=∠ACO=∠AOC,
∴△AOC是等腰直角三角形,
∵AE=8,
∴AO=CO=4,
∴AC=4.
25.
解:证明:(1)如图1,连接OC,
∵DP是O的切线,
∴OC⊥DP,
又∵AD⊥DP,
∴OC∥AD,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
即AC平分∠DAB;
(2)∵PD是O的切线,
∴∠BCP=∠CAB,
又∵CE平分∠ACB,
∴∠ACF=∠BCF,
∴∠CAF+∠ACF=∠BCF+∠PCB,
即∠CFP=∠PCF,
∴PC=PF,即△PCB为等腰三角形;
(2)如图2,连接AE,
∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴AE=BE,
又∵AB为直径,
∴
∵
∴
∴在Rt△ABC中,
∴
∴以BC,BE,AC边的三角形为直角三角形.
