北师大版九年级下册数学 3.4圆周角和圆心角的关系 同步习题(Word版 含解析)
文档属性
| 名称 | 北师大版九年级下册数学 3.4圆周角和圆心角的关系 同步习题(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 211.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
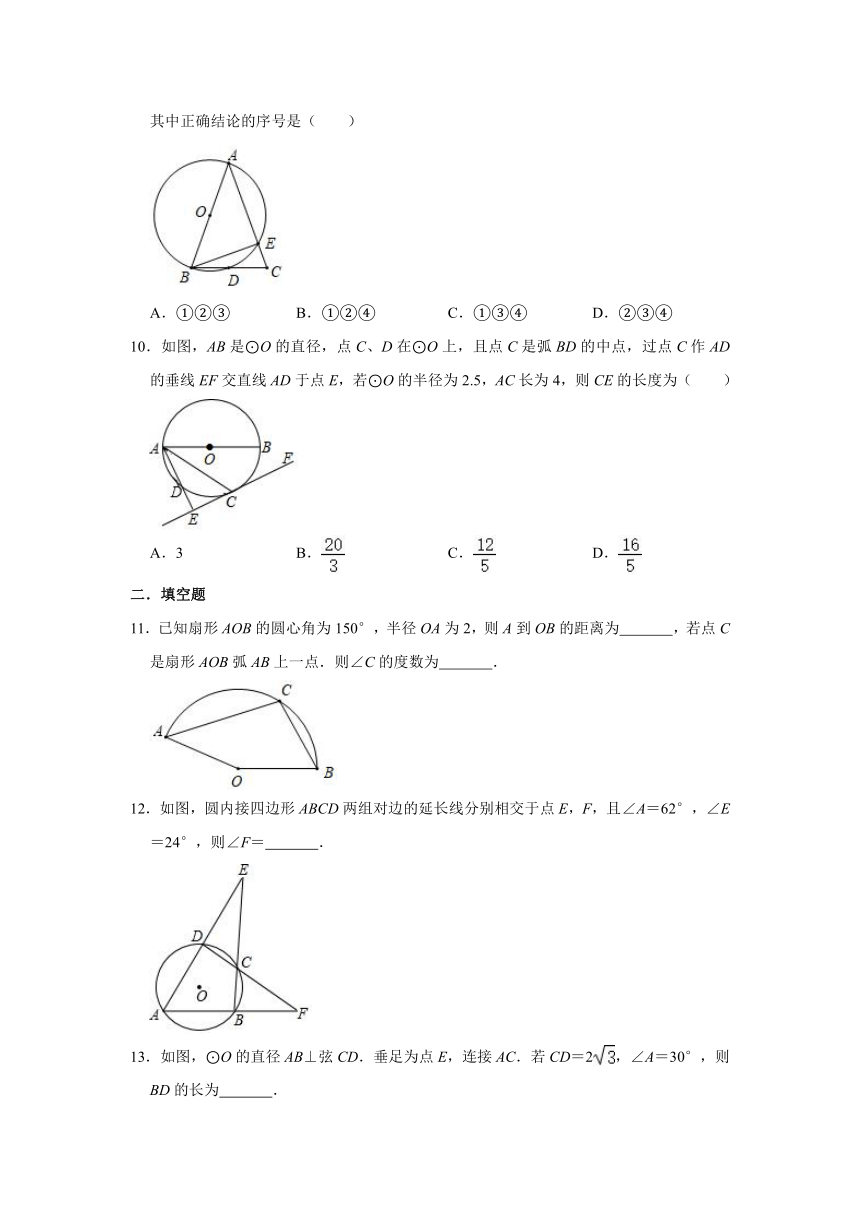
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 00:00:00 | ||
图片预览



文档简介
3.4圆周角和圆心角的关系
一.选择题
1.如图,A、B、C为⊙O上三点,∠BOC=120°,∠2=2∠1,则∠1的度数为( )
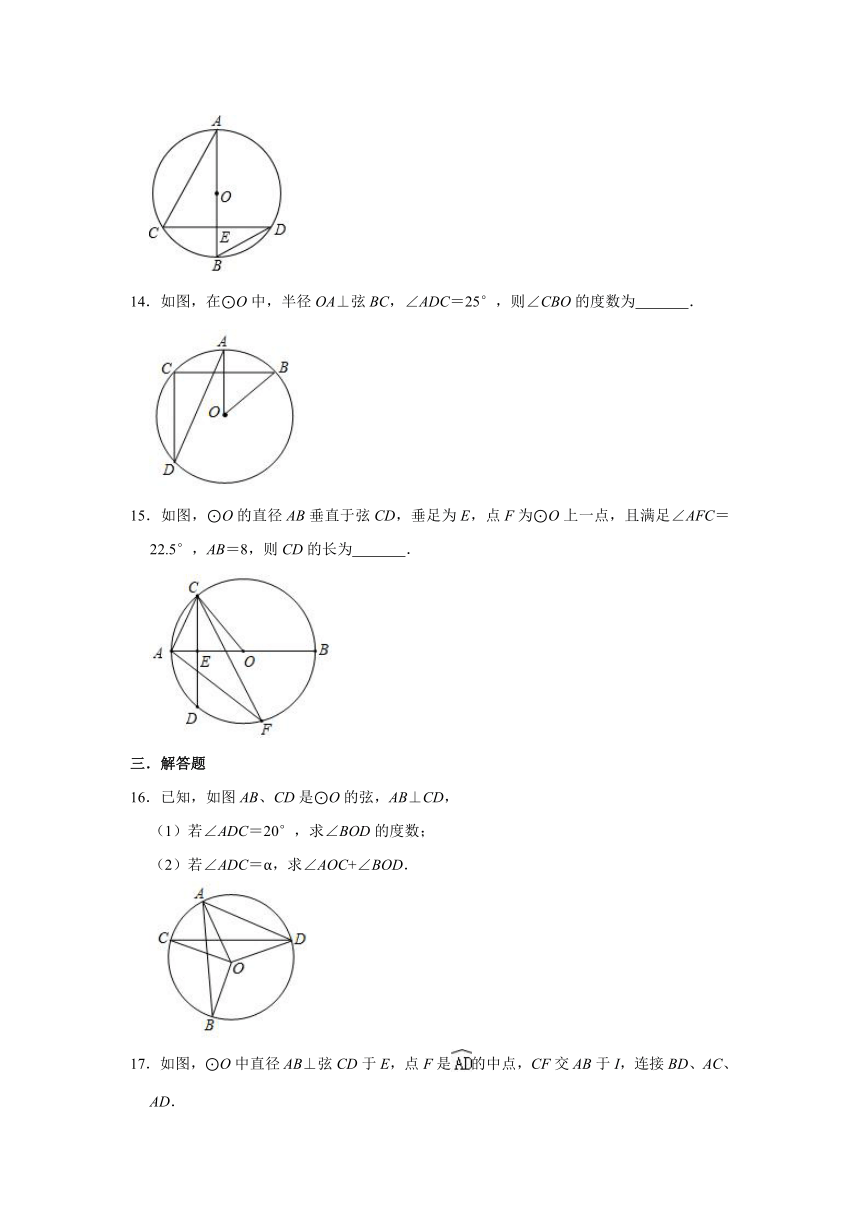
A.20° B.40° C.60° D.120°
2.一弦将圆周分成两弧之比是3:5,则此弦所对的圆周角为( )
A.67.5°或112.5° B.68°或112°
C.67°或113° D.75°或105°
3.如图,MN是半圆O的直径,K是MN延长线上一点,直线KP交半圆于点Q,P.若∠K=20°,∠PMQ=40°,则∠MQP等于( )
A.30° B.35° C.40° D.50°
4.如图,AB是圆O的直径,点C是半圆O上不同于A,B的一点,点D为弧AC的中点,连结OD,BD,AC,设∠CAB=β,∠BDO=α,则( )
A.α=β B.α+2β=90° C.2α+β=90° D.α+β=45°
5.如图,AB是半圆O的直径,D为半圆上的点,在BA延长线上取点C,使得DC=DO,连结CD并延长交圆O于点E,连结AE,若∠C=18°,则∠EAB的度数为( )
A.18° B.21° C.27° D.36°
6.如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=34°,那么∠BAD等于( )
A.34° B.46° C.56° D.66°
7.如图,已知AB是⊙O是直径,弦CD⊥AB,AC=2,BD=1,则sin∠ABD的值是( )
A.2 B. C. D.3
8.如图,四边形ABCD内接于⊙O,连结OA、OC.若∠AOC=120°,则∠B的大小为( )
A.50° B.60° C.80° D.120°
9.已知如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下结论:
①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧是劣弧的2倍.
其中正确结论的序号是( )
A.①②③ B.①②④ C.①③④ D.②③④
10.如图,AB是⊙O的直径,点C、D在⊙O上,且点C是弧BD的中点,过点C作AD的垂线EF交直线AD于点E,若⊙O的半径为2.5,AC长为4,则CE的长度为( )
A.3 B. C. D.
二.填空题
11.已知扇形AOB的圆心角为150°,半径OA为2,则A到OB的距离为 ,若点C是扇形AOB弧AB上一点.则∠C的度数为 .
12.如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=62°,∠E=24°,则∠F= .
13.如图,⊙O的直径AB⊥弦CD.垂足为点E,连接AC.若CD=2,∠A=30°,则BD的长为 .
14.如图,在⊙O中,半径OA⊥弦BC,∠ADC=25°,则∠CBO的度数为 .
15.如图,⊙O的直径AB垂直于弦CD,垂足为E,点F为⊙O上一点,且满足∠AFC=22.5°,AB=8,则CD的长为 .
三.解答题
16.已知,如图AB、CD是⊙O的弦,AB⊥CD,
(1)若∠ADC=20°,求∠BOD的度数;
(2)若∠ADC=α,求∠AOC+∠BOD.
17.如图,⊙O中直径AB⊥弦CD于E,点F是的中点,CF交AB于I,连接BD、AC、AD.
(1)求证:BI=BD;
(2)若OI=1,OE=2,求⊙O的半径.
18.如图,AB是⊙O的直径,M是OA的中点,弦CD⊥AB于点M,连接AD,点E在BC上,∠CDE=45°,DE交AB于点F,CD=6.
(1)求∠OAD的度数;
(2)求DE的长.
参考答案
一.选择题
1.解:∵∠BOC=120°,
∴∠BAC=∠BOC=60°,
∵∠2=2∠1,
∴3∠1=60°,
∴∠1=20°,
故选:A.
2.解:如图,弦AB分⊙O的圆周为3:5,
∴∠AOB=×360°=135°,
∴∠ACB=∠AOB=67.5°,
∴∠ADB=180°﹣∠ACB=112.5°,
∴这条弦所对的圆周角为:67.5°或112.5°.
故选:A.
3.解:连接PO、QO.
根据圆周角定理,得
∠POQ=2∠PMQ=80°,
又OP=OQ,
则∠OPQ=∠OQP=50°,
则∠POM=∠K+∠OPK=70°,
所以∠PQM=∠POM=35°.
故选:B.
4.解:如图,设AC与DO交点为E,如图,
∵OD=OB,
∴∠OBD=∠BDO=α,
∴∠DOA=2∠OBD=2α,
又∵D为中点,AB为⊙O直径,
∴OD⊥AC,
∴∠EAO+∠EOA=90°,
即2α+β=90°.
故选:C.
5.解:如图,连接OE,
∵DC=DO,
∴∠DOC=∠C=18°,
∴∠ODE=∠DOC+∠C=36°,
∵OD=OE,
∴∠OED=∠ODE=36°,
∴∠EOB=∠C+∠OED=18°+36°=54°,
∴∠EAB=∠EOB=27°,
故选:C.
6.解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ACD=34°,
∴∠ABD=34°
∴∠BAD=90°﹣∠ABD=56°,
故选:C.
7.解:∵弦CD⊥AB,AB过O,
∴AB平分CD,
∴BC=BD,
∴∠ABC=∠ABD,
∵BD=1,
∴BC=1,
∵AB为⊙O的直径,
∴∠ACB=90°,
由勾股定理得:AB===3,
∴sin∠ABD=sin∠ABC==,
故选:C.
8.解:∵∠AOC=120°,
∴∠D=AOC=60°,
∴∠B=180°﹣∠D=120°,
故选:D.
9.解:①∵∠A=45°,AB是直径,
∴∠AEB=90°,
∴∠ABE=45°,
∵AB=AC,
∴∠ABC=∠ACB=67.5°,
∴∠EBC=67.5°﹣45°=22.5°,
此选项正确;
②连接AD,
∵AB=AC,AB是直径,
∴∠ADB=90°,
∴BD=CD,
此选项正确;
③∵AB是直径,
∴∠AEB=90°,
由①知∠EBC=22.5°,∠C=67.5°,
∴BE=tan67.5°?CE,
∴BE≠2CE,
在Rt△ABE中,∠AEB=90°,∠BAE=45°,
∴∠ABE=45°,
∴AE=BE,
∴AE≠2CE,
此选项错误;
④∵∠ABE=45°,∠BAD=22.5°,
∴劣弧AE=2劣弧BD,
∵劣弧BD=劣弧DE,
∴劣弧AE=2劣弧DE,
此选项正确.
正确的有①②④,
故选:B.
10.解:连接BC,
∵点C是弧BD的中点,
∴∠EAC=∠CAB,
又∵AB为直径,AE⊥EF,
∴∠AEC=∠ACB=90°,
∴△EAC∽△CAB,
∴,
∴=.
故选:C.
二.填空题
11.解:作AH⊥OB于H,作弧ACB所对的圆周角∠ADB,如图,
∵∠AOB=150°,
∴∠AOH=30°,
∴AH=OA=1,
即点A到OB的距离为1;
∵∠D=∠AOB=×150°=75°,
而∠C+∠D=180°,
∴∠C=180°﹣75°=105°.
故答案为1,105°.
12.解:∵四边形ABCD是圆内接四边形,
∴∠BCF=∠A=62°,
∵∠CBF是△ABE的一个外角,
∴∠CBF=∠A+∠E=62°+24°=86°,
∴∠F=180°﹣∠BCF﹣∠CBF=180°﹣62°﹣86°=32°,
故答案为32°.
13.解:如图所示,则∠BDC=∠A=30°,
∵AB⊥CD,
∴CE=DE=CD=,∠BED=90°,
∴BD=2BE,
设BE=x,则BD=2x,
由勾股定理得:BD2=BE2+ED2,
,
x=1,
∴BD=2,
故答案为:2.
14.解:∵半径OA⊥弦BC,
∴=,
∴∠AOB=2∠ADC=50°,
∴∠CBO=90°﹣50°=40°.
故答案为40°.
15.解:∵∠AOC=2∠AFC=45°,
∴∠BOC=2∠A=45°,
∵⊙O的直径AB垂直于弦CD,
∴CE=DE,△OCE为等腰直角三角形,
∴CE=OC=2,
∴CD=2CE=4.
故答案为4
三.解答题
16.解:(1)∵AB⊥CD,
∴∠BAD+∠ADC=90°,
∴∠BAD=90°﹣20°=70°,
∴∠BOD=2∠BAD=2×70°=140°;
(2)∵∠BAD+∠ADC=90°,
∴∠BAD=90°﹣α,
∴∠BOD=2∠BAD=2(90°﹣α)=180°﹣2α;
∵∠AOC=2∠ADC=2α,
∴∠AOC+∠BOD=2α+180°﹣2α=180°.
17.(1)证明:如图,连接DI,
∵AB为⊙O的直径,且AB⊥CD,
∴,
∴∠CAB=∠BAD,∠BAD=∠BDC,
∵点F是的中点,
∴∠ACF=∠DCF,
∴I是△ADC的内心,
∴∠ADI=∠CDI,
∵∠BID=∠BAD+∠ADI,∠BDI=∠BDC+∠CDI,
∴∠BID=∠BDI,
∴BI=BD;
(2)连接OD,
设⊙O的半径为r,
∵OI=1,OE=2,
∴BE=r﹣2,BD=BE=r+2,
由勾股定理得:DE2=r2﹣22=(r+1)2﹣(r﹣2)2,
r2﹣6r﹣1=0,
r1=3+,r2=3﹣(舍),
答:⊙O的半径是3+.
18.解:(1)连接OD.
∵DC⊥OA,AM=MO,
∴DA=DO,
∵OA=OD,
∴OA=OD=AD,
∴△AOD是等边三角形,
∴∠OAD=60°.
(2)连接OC,CF,EC.
∵OA⊥CD,
∴=,CM=DM,
∴∠AOC=∠AOD=60°,FC=FD,
∵∠CDE=45°,
∴CF=DF,FM=CM=DM=3,DF=FC=3,
∵∠CED=∠COD=60°,∠CFE=90°,
∴EF=CF=,
∴DE=EF+DF=+3.
一.选择题
1.如图,A、B、C为⊙O上三点,∠BOC=120°,∠2=2∠1,则∠1的度数为( )
A.20° B.40° C.60° D.120°
2.一弦将圆周分成两弧之比是3:5,则此弦所对的圆周角为( )
A.67.5°或112.5° B.68°或112°
C.67°或113° D.75°或105°
3.如图,MN是半圆O的直径,K是MN延长线上一点,直线KP交半圆于点Q,P.若∠K=20°,∠PMQ=40°,则∠MQP等于( )
A.30° B.35° C.40° D.50°
4.如图,AB是圆O的直径,点C是半圆O上不同于A,B的一点,点D为弧AC的中点,连结OD,BD,AC,设∠CAB=β,∠BDO=α,则( )
A.α=β B.α+2β=90° C.2α+β=90° D.α+β=45°
5.如图,AB是半圆O的直径,D为半圆上的点,在BA延长线上取点C,使得DC=DO,连结CD并延长交圆O于点E,连结AE,若∠C=18°,则∠EAB的度数为( )
A.18° B.21° C.27° D.36°
6.如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=34°,那么∠BAD等于( )
A.34° B.46° C.56° D.66°
7.如图,已知AB是⊙O是直径,弦CD⊥AB,AC=2,BD=1,则sin∠ABD的值是( )
A.2 B. C. D.3
8.如图,四边形ABCD内接于⊙O,连结OA、OC.若∠AOC=120°,则∠B的大小为( )
A.50° B.60° C.80° D.120°
9.已知如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下结论:
①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧是劣弧的2倍.
其中正确结论的序号是( )
A.①②③ B.①②④ C.①③④ D.②③④
10.如图,AB是⊙O的直径,点C、D在⊙O上,且点C是弧BD的中点,过点C作AD的垂线EF交直线AD于点E,若⊙O的半径为2.5,AC长为4,则CE的长度为( )
A.3 B. C. D.
二.填空题
11.已知扇形AOB的圆心角为150°,半径OA为2,则A到OB的距离为 ,若点C是扇形AOB弧AB上一点.则∠C的度数为 .
12.如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=62°,∠E=24°,则∠F= .
13.如图,⊙O的直径AB⊥弦CD.垂足为点E,连接AC.若CD=2,∠A=30°,则BD的长为 .
14.如图,在⊙O中,半径OA⊥弦BC,∠ADC=25°,则∠CBO的度数为 .
15.如图,⊙O的直径AB垂直于弦CD,垂足为E,点F为⊙O上一点,且满足∠AFC=22.5°,AB=8,则CD的长为 .
三.解答题
16.已知,如图AB、CD是⊙O的弦,AB⊥CD,
(1)若∠ADC=20°,求∠BOD的度数;
(2)若∠ADC=α,求∠AOC+∠BOD.
17.如图,⊙O中直径AB⊥弦CD于E,点F是的中点,CF交AB于I,连接BD、AC、AD.
(1)求证:BI=BD;
(2)若OI=1,OE=2,求⊙O的半径.
18.如图,AB是⊙O的直径,M是OA的中点,弦CD⊥AB于点M,连接AD,点E在BC上,∠CDE=45°,DE交AB于点F,CD=6.
(1)求∠OAD的度数;
(2)求DE的长.
参考答案
一.选择题
1.解:∵∠BOC=120°,
∴∠BAC=∠BOC=60°,
∵∠2=2∠1,
∴3∠1=60°,
∴∠1=20°,
故选:A.
2.解:如图,弦AB分⊙O的圆周为3:5,
∴∠AOB=×360°=135°,
∴∠ACB=∠AOB=67.5°,
∴∠ADB=180°﹣∠ACB=112.5°,
∴这条弦所对的圆周角为:67.5°或112.5°.
故选:A.
3.解:连接PO、QO.
根据圆周角定理,得
∠POQ=2∠PMQ=80°,
又OP=OQ,
则∠OPQ=∠OQP=50°,
则∠POM=∠K+∠OPK=70°,
所以∠PQM=∠POM=35°.
故选:B.
4.解:如图,设AC与DO交点为E,如图,
∵OD=OB,
∴∠OBD=∠BDO=α,
∴∠DOA=2∠OBD=2α,
又∵D为中点,AB为⊙O直径,
∴OD⊥AC,
∴∠EAO+∠EOA=90°,
即2α+β=90°.
故选:C.
5.解:如图,连接OE,
∵DC=DO,
∴∠DOC=∠C=18°,
∴∠ODE=∠DOC+∠C=36°,
∵OD=OE,
∴∠OED=∠ODE=36°,
∴∠EOB=∠C+∠OED=18°+36°=54°,
∴∠EAB=∠EOB=27°,
故选:C.
6.解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ACD=34°,
∴∠ABD=34°
∴∠BAD=90°﹣∠ABD=56°,
故选:C.
7.解:∵弦CD⊥AB,AB过O,
∴AB平分CD,
∴BC=BD,
∴∠ABC=∠ABD,
∵BD=1,
∴BC=1,
∵AB为⊙O的直径,
∴∠ACB=90°,
由勾股定理得:AB===3,
∴sin∠ABD=sin∠ABC==,
故选:C.
8.解:∵∠AOC=120°,
∴∠D=AOC=60°,
∴∠B=180°﹣∠D=120°,
故选:D.
9.解:①∵∠A=45°,AB是直径,
∴∠AEB=90°,
∴∠ABE=45°,
∵AB=AC,
∴∠ABC=∠ACB=67.5°,
∴∠EBC=67.5°﹣45°=22.5°,
此选项正确;
②连接AD,
∵AB=AC,AB是直径,
∴∠ADB=90°,
∴BD=CD,
此选项正确;
③∵AB是直径,
∴∠AEB=90°,
由①知∠EBC=22.5°,∠C=67.5°,
∴BE=tan67.5°?CE,
∴BE≠2CE,
在Rt△ABE中,∠AEB=90°,∠BAE=45°,
∴∠ABE=45°,
∴AE=BE,
∴AE≠2CE,
此选项错误;
④∵∠ABE=45°,∠BAD=22.5°,
∴劣弧AE=2劣弧BD,
∵劣弧BD=劣弧DE,
∴劣弧AE=2劣弧DE,
此选项正确.
正确的有①②④,
故选:B.
10.解:连接BC,
∵点C是弧BD的中点,
∴∠EAC=∠CAB,
又∵AB为直径,AE⊥EF,
∴∠AEC=∠ACB=90°,
∴△EAC∽△CAB,
∴,
∴=.
故选:C.
二.填空题
11.解:作AH⊥OB于H,作弧ACB所对的圆周角∠ADB,如图,
∵∠AOB=150°,
∴∠AOH=30°,
∴AH=OA=1,
即点A到OB的距离为1;
∵∠D=∠AOB=×150°=75°,
而∠C+∠D=180°,
∴∠C=180°﹣75°=105°.
故答案为1,105°.
12.解:∵四边形ABCD是圆内接四边形,
∴∠BCF=∠A=62°,
∵∠CBF是△ABE的一个外角,
∴∠CBF=∠A+∠E=62°+24°=86°,
∴∠F=180°﹣∠BCF﹣∠CBF=180°﹣62°﹣86°=32°,
故答案为32°.
13.解:如图所示,则∠BDC=∠A=30°,
∵AB⊥CD,
∴CE=DE=CD=,∠BED=90°,
∴BD=2BE,
设BE=x,则BD=2x,
由勾股定理得:BD2=BE2+ED2,
,
x=1,
∴BD=2,
故答案为:2.
14.解:∵半径OA⊥弦BC,
∴=,
∴∠AOB=2∠ADC=50°,
∴∠CBO=90°﹣50°=40°.
故答案为40°.
15.解:∵∠AOC=2∠AFC=45°,
∴∠BOC=2∠A=45°,
∵⊙O的直径AB垂直于弦CD,
∴CE=DE,△OCE为等腰直角三角形,
∴CE=OC=2,
∴CD=2CE=4.
故答案为4
三.解答题
16.解:(1)∵AB⊥CD,
∴∠BAD+∠ADC=90°,
∴∠BAD=90°﹣20°=70°,
∴∠BOD=2∠BAD=2×70°=140°;
(2)∵∠BAD+∠ADC=90°,
∴∠BAD=90°﹣α,
∴∠BOD=2∠BAD=2(90°﹣α)=180°﹣2α;
∵∠AOC=2∠ADC=2α,
∴∠AOC+∠BOD=2α+180°﹣2α=180°.
17.(1)证明:如图,连接DI,
∵AB为⊙O的直径,且AB⊥CD,
∴,
∴∠CAB=∠BAD,∠BAD=∠BDC,
∵点F是的中点,
∴∠ACF=∠DCF,
∴I是△ADC的内心,
∴∠ADI=∠CDI,
∵∠BID=∠BAD+∠ADI,∠BDI=∠BDC+∠CDI,
∴∠BID=∠BDI,
∴BI=BD;
(2)连接OD,
设⊙O的半径为r,
∵OI=1,OE=2,
∴BE=r﹣2,BD=BE=r+2,
由勾股定理得:DE2=r2﹣22=(r+1)2﹣(r﹣2)2,
r2﹣6r﹣1=0,
r1=3+,r2=3﹣(舍),
答:⊙O的半径是3+.
18.解:(1)连接OD.
∵DC⊥OA,AM=MO,
∴DA=DO,
∵OA=OD,
∴OA=OD=AD,
∴△AOD是等边三角形,
∴∠OAD=60°.
(2)连接OC,CF,EC.
∵OA⊥CD,
∴=,CM=DM,
∴∠AOC=∠AOD=60°,FC=FD,
∵∠CDE=45°,
∴CF=DF,FM=CM=DM=3,DF=FC=3,
∵∠CED=∠COD=60°,∠CFE=90°,
∴EF=CF=,
∴DE=EF+DF=+3.
