19.1.2平行四边形的判定(1)
文档属性
| 名称 | 19.1.2平行四边形的判定(1) |

|
|
| 格式 | rar | ||
| 文件大小 | 600.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-26 00:00:00 | ||
图片预览


文档简介
(共29张PPT)
19.1.2
平行四边形的判定(1)
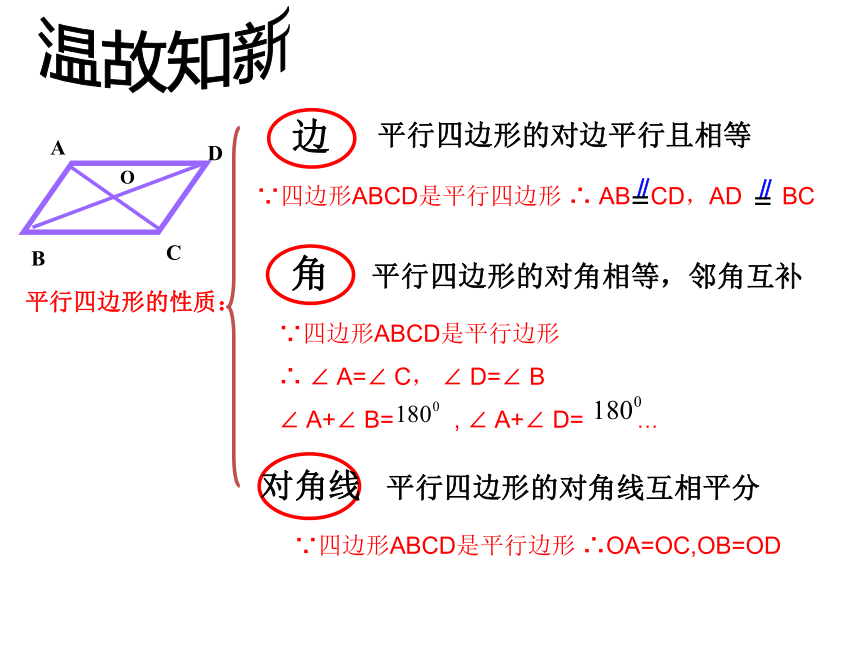
边
平行四边形的对边平行且相等
角
对角线
平行四边形的对角线互相平分
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边形 ∴ AB CD,AD BC
∥
﹦
∥
﹦
平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= , ∠ A+∠ D= …
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD
我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
(1)根据定义:两组对边分别平行的四边形叫做平行四边形
因为AB//CD,AD//BC;
所以四边形ABCD是平行四边形。
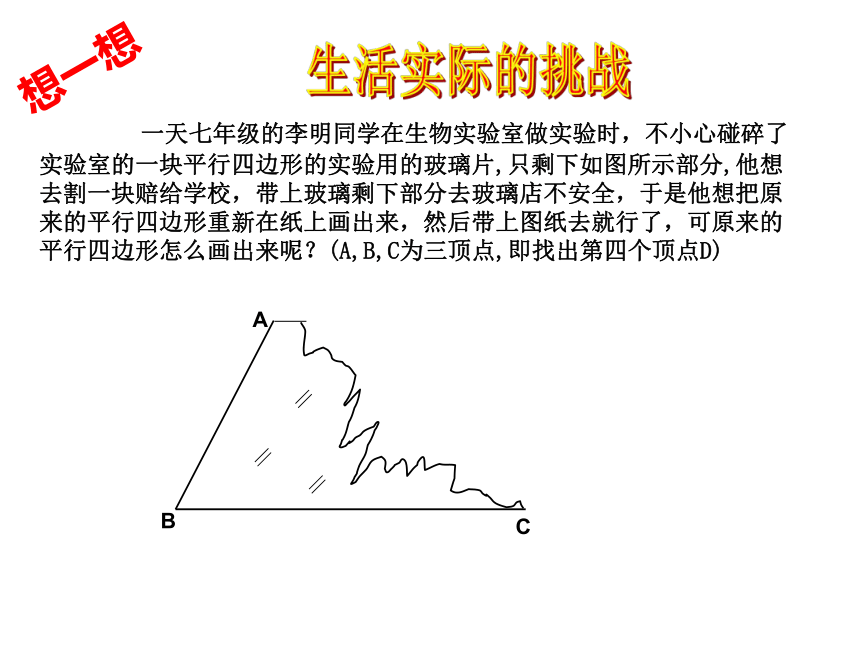
一天七年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)
A
B
C
想一想
D
A
B
C
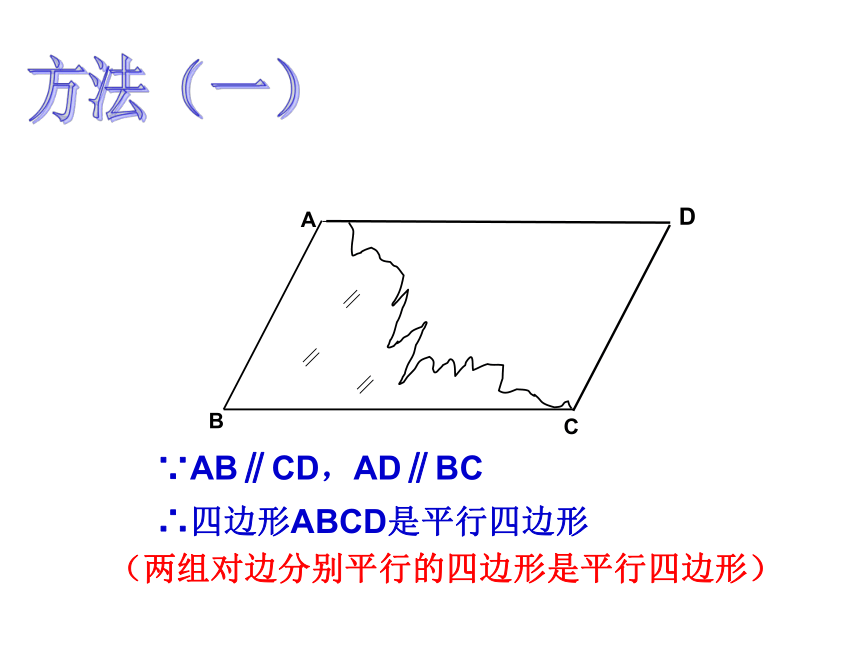
(两组对边分别平行的四边形是平行四边形)
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
D
A
B
C
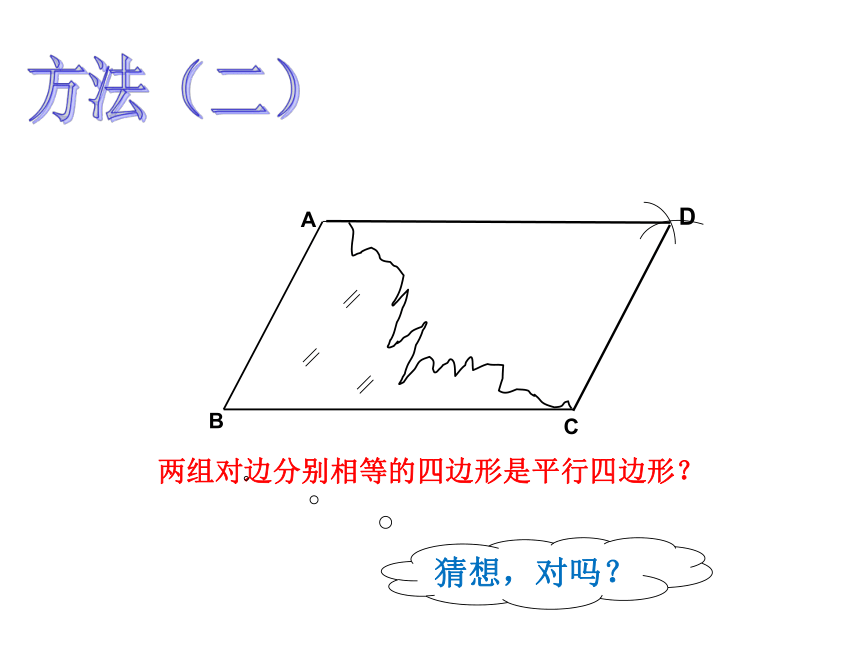
两组对边分别相等的四边形是平行四边形?
猜想,对吗?
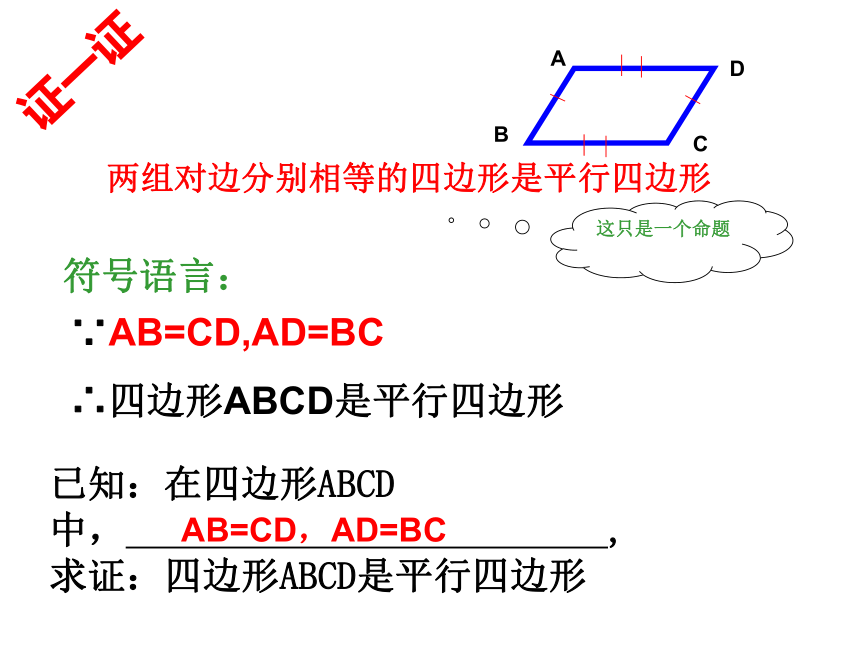
两组对边分别相等的四边形是平行四边形
这只是一个命题
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
已知:在四边形ABCD中, ,
求证:四边形ABCD是平行四边形
A
B
C
D
符号语言:
AB=CD,AD=BC
证一证
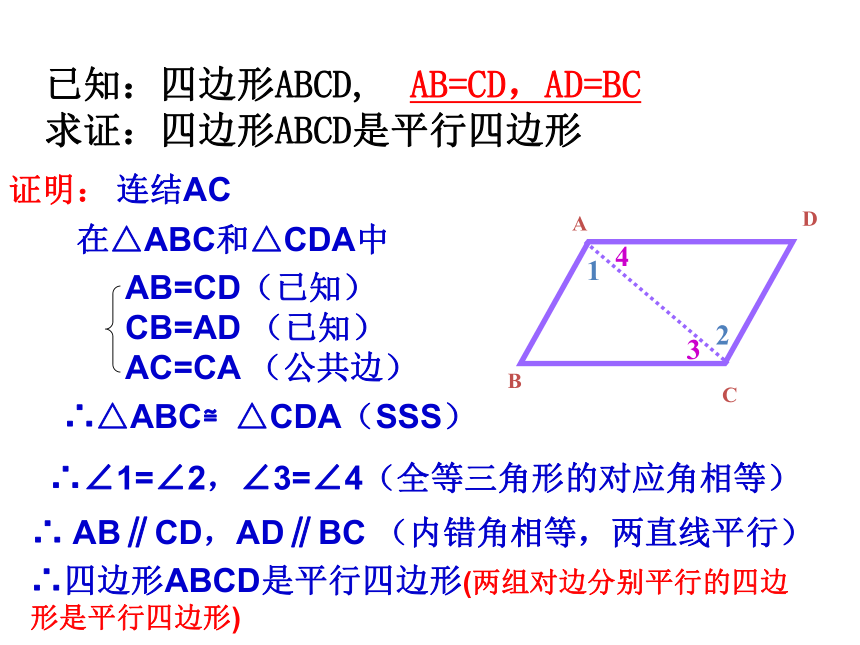
已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形
证明:
连结AC
在△ABC和△CDA中
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
D
B
A
C
2
1
3
4
AB=CD(已知)
CB=AD (已知)
AC=CA (公共边)
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
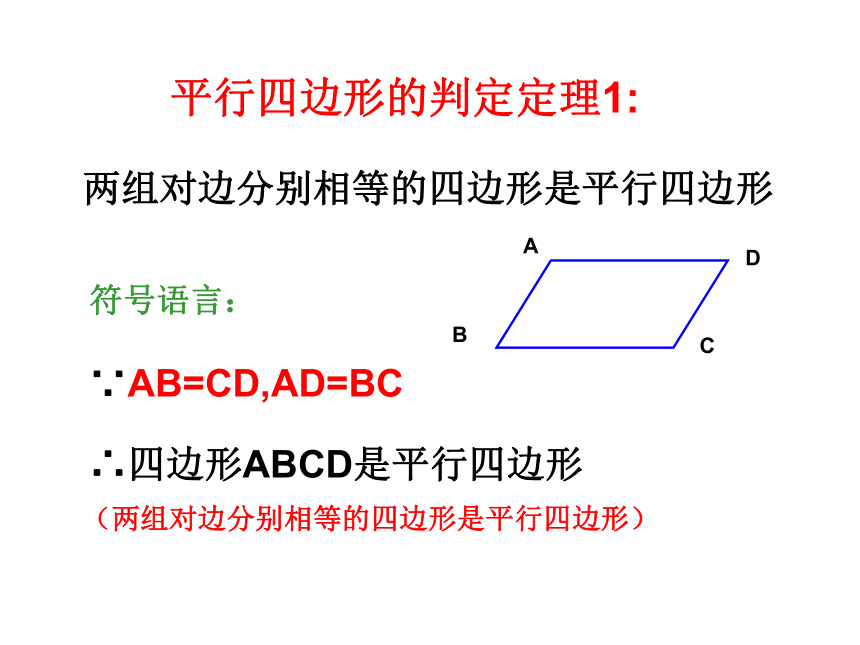
两组对边分别相等的四边形是平行四边形
平行四边形的判定定理1:
符号语言:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
A
B
C
D
D
A
B
C
A
B
C
D
一组对边平行且相等的四边形是平行四边形?
∵AB CD, ∴四边形ABCD是平行四边形
∥
﹦
猜想,对吗?
A
B
C
D
求证:四边形ABCD是平行四边形。
证明:连接AC
∵AD∥BC
∴∠DAC=∠ACB
又∵AD=BC,AC=AC,
∴ΔABC≌ΔCDA
∴∠BAC=∠ACD
∴AB∥CD
∴四边形ABCD是平行四边形
已知:在四边形ABCD中, AD BC。
(两组对边分别平行的四边形是平行四边形)
你还有其他证法吗?
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理2:
符号语言:
∵AB CD
∴四边形ABCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
A
B
C
D
D
A
B
C
两组对角分别相等的四边形是平行四边形?
猜想,对吗?
已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
证明:
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °
∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)
A
B
C
D
两组对角分别相等的四边形是平行四边形
平行四边形的判定定理3:
符号语言:
A
B
C
D
∵∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形
(两组对角分别相等的四边形是平行四边形)
D
O
A
B
C
对角线互相平分的四边形是平行四边形?
猜想,对吗?
O
已知:四边形ABCD, 对角线AC、BD相交于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
证明:
在△AOD和△COB中
OA=OC(已知)
∠AOD=∠COB (对顶角相等)
OD=OB (已知)
∴△AOD≌△COB(SAS)
∴∠1=∠2 AD=CB(全等三角形的对应角、对应边相等)
∴ AD∥CB(内错角相等,两直线平行)
∴四边形ABCD是平行四边形
B
A
C
2
1
D
(一组对边平行且相等的四边形是平行四边形)
对角线互相平分的四边形是平行四边形
平行四边形的判定定理4:
符号语言:
A
B
C
D
O
∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形)
从边来判定
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
理一理
平行四边形的判定方法
1、请你向同学们展示一下你的作品-----平行四边形,同时也向同学简要介绍一下你制作的过程,为什么你能确定你制作的四边形一定是平行四边形 理由是什么?
试一试
2.如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?
AB ∥ DC∥ EF
AD ∥ BC
DE ∥ CF
3、请你识别下列四边形哪些是平行四边形 为什么?
A
D
C
B
110°
70°
110°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
4、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠C
D
B
D
A
C
(两组对边分别平行)
(两组对边分别相等)
(一组对边平行且相等)
(两组对角分别相等)
A
B
D
C
大显身手
D
A
B
C
E
F
证法1:
四边形ABCD是平行四边形
AD ∥ BC且AD =BC
EAD= FCB
AE=CF
EAD= FCB
AD=BC
AED ≌ CFB(SAS)
DE=BF
四边形BFDE是平行四边形
在 AED和 CFB中
同理可证:BE=DF
1.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
大显身手
1.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
证法2:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
2.已知:如图,E,F分别是 的边AD,BC的中点。
求证:BE=DF.
D
F
E
C
B
A
证明:
∵四边形ABCD是平行四边形,
∴AB∥CD (平行四边形的定义)
AD=BC(平行四边形的对边分别相等),
∵E,F分别是AD,BC的中点,
∴ED=BF,即ED BF.
∥
﹦
∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。
∴BE=DF(平行四边形的对边分别相等)。
ABCD
Y
说一说:
1.本节课你学会了几种平行四边形的判定方法
2.本节课所学的解决问题的思路是:
(2)碰到平行四边形的问题常转化为三角形来解决。
(1)解决一个数学问题,常要通过“动手实践”----“ 猜想”----“验证猜想(证明)”-----“得出结论”
作业布置:
课本P91 4、5、10
19.1.2
平行四边形的判定(1)
边
平行四边形的对边平行且相等
角
对角线
平行四边形的对角线互相平分
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边形 ∴ AB CD,AD BC
∥
﹦
∥
﹦
平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= , ∠ A+∠ D= …
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD
我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
(1)根据定义:两组对边分别平行的四边形叫做平行四边形
因为AB//CD,AD//BC;
所以四边形ABCD是平行四边形。
一天七年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)
A
B
C
想一想
D
A
B
C
(两组对边分别平行的四边形是平行四边形)
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
D
A
B
C
两组对边分别相等的四边形是平行四边形?
猜想,对吗?
两组对边分别相等的四边形是平行四边形
这只是一个命题
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
已知:在四边形ABCD中, ,
求证:四边形ABCD是平行四边形
A
B
C
D
符号语言:
AB=CD,AD=BC
证一证
已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形
证明:
连结AC
在△ABC和△CDA中
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
D
B
A
C
2
1
3
4
AB=CD(已知)
CB=AD (已知)
AC=CA (公共边)
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
两组对边分别相等的四边形是平行四边形
平行四边形的判定定理1:
符号语言:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
A
B
C
D
D
A
B
C
A
B
C
D
一组对边平行且相等的四边形是平行四边形?
∵AB CD, ∴四边形ABCD是平行四边形
∥
﹦
猜想,对吗?
A
B
C
D
求证:四边形ABCD是平行四边形。
证明:连接AC
∵AD∥BC
∴∠DAC=∠ACB
又∵AD=BC,AC=AC,
∴ΔABC≌ΔCDA
∴∠BAC=∠ACD
∴AB∥CD
∴四边形ABCD是平行四边形
已知:在四边形ABCD中, AD BC。
(两组对边分别平行的四边形是平行四边形)
你还有其他证法吗?
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理2:
符号语言:
∵AB CD
∴四边形ABCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
A
B
C
D
D
A
B
C
两组对角分别相等的四边形是平行四边形?
猜想,对吗?
已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
证明:
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °
∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)
A
B
C
D
两组对角分别相等的四边形是平行四边形
平行四边形的判定定理3:
符号语言:
A
B
C
D
∵∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形
(两组对角分别相等的四边形是平行四边形)
D
O
A
B
C
对角线互相平分的四边形是平行四边形?
猜想,对吗?
O
已知:四边形ABCD, 对角线AC、BD相交于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
证明:
在△AOD和△COB中
OA=OC(已知)
∠AOD=∠COB (对顶角相等)
OD=OB (已知)
∴△AOD≌△COB(SAS)
∴∠1=∠2 AD=CB(全等三角形的对应角、对应边相等)
∴ AD∥CB(内错角相等,两直线平行)
∴四边形ABCD是平行四边形
B
A
C
2
1
D
(一组对边平行且相等的四边形是平行四边形)
对角线互相平分的四边形是平行四边形
平行四边形的判定定理4:
符号语言:
A
B
C
D
O
∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形)
从边来判定
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
理一理
平行四边形的判定方法
1、请你向同学们展示一下你的作品-----平行四边形,同时也向同学简要介绍一下你制作的过程,为什么你能确定你制作的四边形一定是平行四边形 理由是什么?
试一试
2.如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?
AB ∥ DC∥ EF
AD ∥ BC
DE ∥ CF
3、请你识别下列四边形哪些是平行四边形 为什么?
A
D
C
B
110°
70°
110°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
4、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠C
D
B
D
A
C
(两组对边分别平行)
(两组对边分别相等)
(一组对边平行且相等)
(两组对角分别相等)
A
B
D
C
大显身手
D
A
B
C
E
F
证法1:
四边形ABCD是平行四边形
AD ∥ BC且AD =BC
EAD= FCB
AE=CF
EAD= FCB
AD=BC
AED ≌ CFB(SAS)
DE=BF
四边形BFDE是平行四边形
在 AED和 CFB中
同理可证:BE=DF
1.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
大显身手
1.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
证法2:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
2.已知:如图,E,F分别是 的边AD,BC的中点。
求证:BE=DF.
D
F
E
C
B
A
证明:
∵四边形ABCD是平行四边形,
∴AB∥CD (平行四边形的定义)
AD=BC(平行四边形的对边分别相等),
∵E,F分别是AD,BC的中点,
∴ED=BF,即ED BF.
∥
﹦
∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。
∴BE=DF(平行四边形的对边分别相等)。
ABCD
Y
说一说:
1.本节课你学会了几种平行四边形的判定方法
2.本节课所学的解决问题的思路是:
(2)碰到平行四边形的问题常转化为三角形来解决。
(1)解决一个数学问题,常要通过“动手实践”----“ 猜想”----“验证猜想(证明)”-----“得出结论”
作业布置:
课本P91 4、5、10
