勾股定理的应用
图片预览





文档简介
(共15张PPT)
回顾与思考
-----------勾股定理
直角三角形的边、角之间分别存在着什么关系?
课堂练习: 一.判断题. 1. ABC的两边AB=5,AC=12,则BC=13 ( )
2. ABC的a=6,b=8,则c=10 ( )
二.填空题 1.在 ABC中, ∠C=90°, (1)若c=10,a:b=3:4,则a=____,b=___.
(2)若a=9,b=40,则c=______. 2.在 ABC中, ∠ C=90°,若AC=6,CB=8,则 ABC面积为_____,斜边上的高为______.
6
8
41
24
4.8
3.若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( )
A. 12 cm B. 10 cm C. 8 cm D. 6 cm
D
4、已知:数7和24,请你再写一个整数,
使这些数恰好是一个直角三角形三边的长,
则这个数可以是——
5、一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是————
25
24
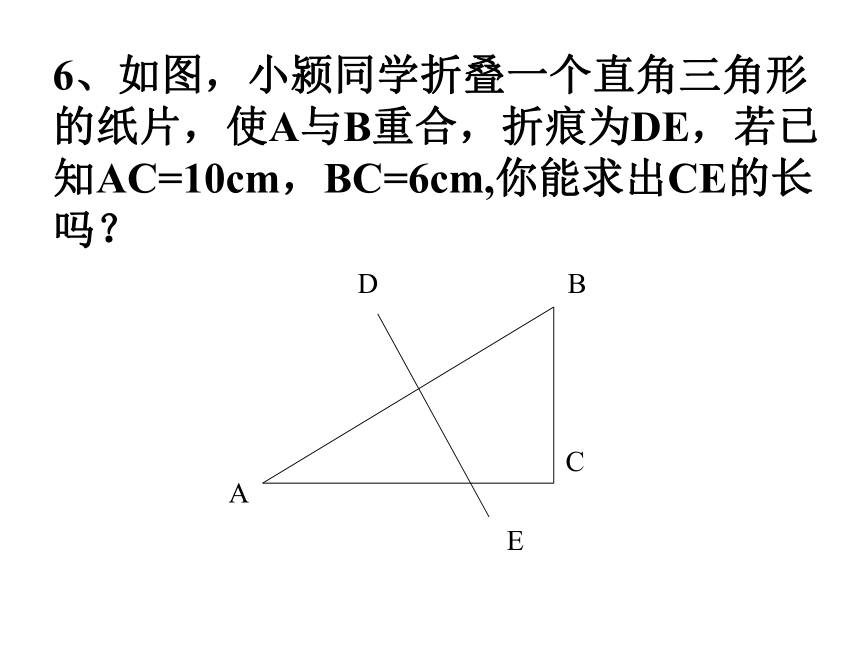
6、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
7、折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求 1)CF 的长; 2)EC的长.
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
8、如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
9如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )
A.20cm B.10cm C.14cm D.无法确定
B
B
8
O
A
2
蛋糕
A
C
B
8
周长的一半
6
10、假期中,王强和同学到某海岛上去玩探宝游戏,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,在折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A 到宝藏埋藏点B的距离是多少千米?
A
B
8
2
3
6
1
11、小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
A
B
C
5米
(X+1)米
x米
试一试:
在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
D
A
B
C
原文是:
今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深、葭长各几何?
12. 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD
A
B
C
D
证明:
过A作AE⊥BC于E
E
∵AB=AC,∴BE=CE
在Rt △ADE中,
AD2=AE2+DE2
在Rt △ABE中,
AB2=AE2+BE2
∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
= DE2- BE2
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
=BD·CD
7、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求以折痕EF为边长的正方形面积。
A
B
C
D
G
F
E
回顾与思考
-----------勾股定理
直角三角形的边、角之间分别存在着什么关系?
课堂练习: 一.判断题. 1. ABC的两边AB=5,AC=12,则BC=13 ( )
2. ABC的a=6,b=8,则c=10 ( )
二.填空题 1.在 ABC中, ∠C=90°, (1)若c=10,a:b=3:4,则a=____,b=___.
(2)若a=9,b=40,则c=______. 2.在 ABC中, ∠ C=90°,若AC=6,CB=8,则 ABC面积为_____,斜边上的高为______.
6
8
41
24
4.8
3.若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( )
A. 12 cm B. 10 cm C. 8 cm D. 6 cm
D
4、已知:数7和24,请你再写一个整数,
使这些数恰好是一个直角三角形三边的长,
则这个数可以是——
5、一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是————
25
24
6、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
7、折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求 1)CF 的长; 2)EC的长.
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
8、如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
9如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )
A.20cm B.10cm C.14cm D.无法确定
B
B
8
O
A
2
蛋糕
A
C
B
8
周长的一半
6
10、假期中,王强和同学到某海岛上去玩探宝游戏,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,在折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A 到宝藏埋藏点B的距离是多少千米?
A
B
8
2
3
6
1
11、小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
A
B
C
5米
(X+1)米
x米
试一试:
在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
D
A
B
C
原文是:
今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深、葭长各几何?
12. 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD
A
B
C
D
证明:
过A作AE⊥BC于E
E
∵AB=AC,∴BE=CE
在Rt △ADE中,
AD2=AE2+DE2
在Rt △ABE中,
AB2=AE2+BE2
∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
= DE2- BE2
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
=BD·CD
7、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求以折痕EF为边长的正方形面积。
A
B
C
D
G
F
E
