6.4 确定一次函数的表达式 同步练习(含答案)
文档属性
| 名称 | 6.4 确定一次函数的表达式 同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 一次函数
4 确定一次函数的表达式
夯实基础
知识点一 求正比例函数的表达式
1.已知y与x成正比例,且x=3时,y=2,则y=3时,x的值为( )
A. B. C.2 D.12
2.如图,直线所表示的变量x,y之间的函数关系式为( )
A.y=-2x B.y=2x C.y=-x D.y=x
3.已知y与2x成正比例,且当x=3时,y=-12.
(1)求y与x之间的函数表达式;
(2)求当x=5时y的值.
知识点二 求一次函数的表达式
4.已知直线经过点A(4,0),B(0,3),则直线的函数表达式为( )
A.y=-x+3 B.y=3x+4 C.y=4x+3 D.y=-3x+3
5.已知y是x的一次函数,下表中列出了部分对应值,则m等于( )
x -1 0 1
y 1 -2 m
A.-1 B.0 C.-5 D.
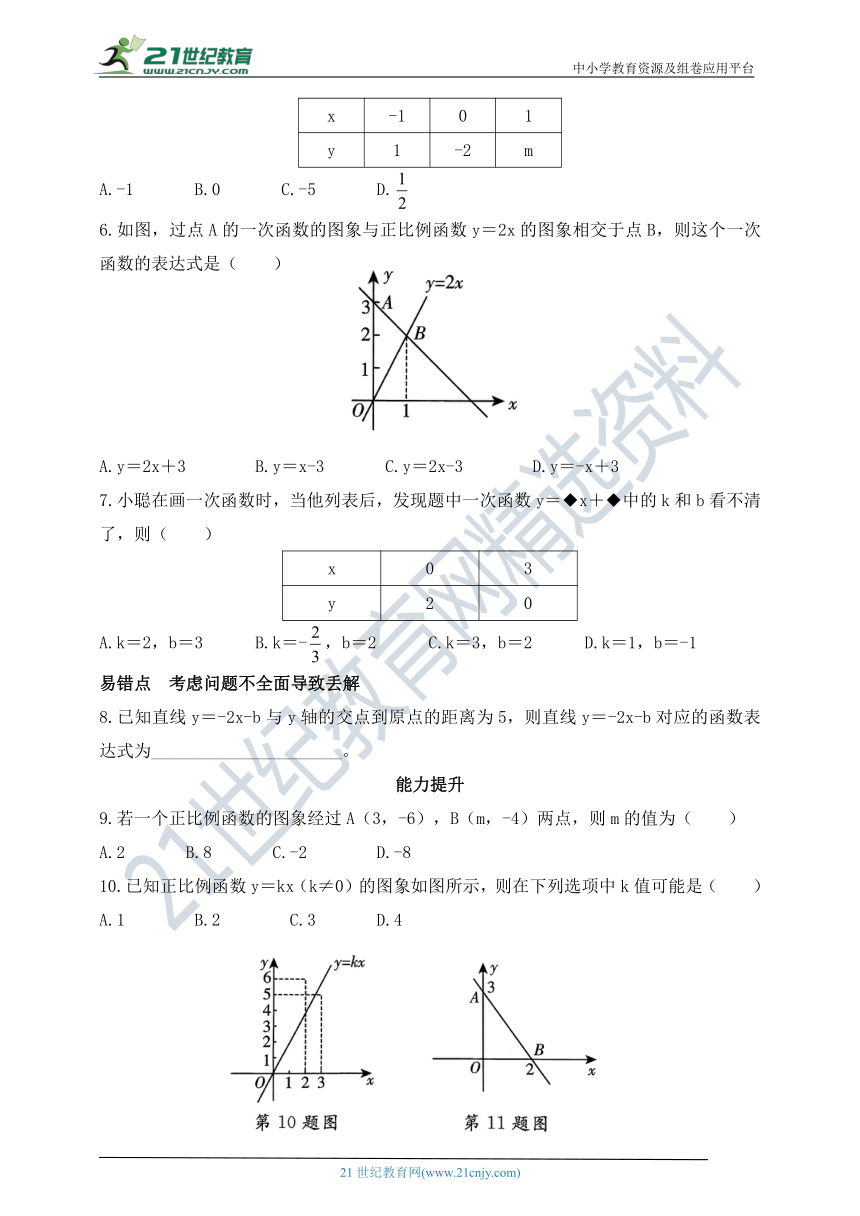
6.如图,过点A的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的表达式是( )
A.y=2x+3 B.y=x-3 C.y=2x-3 D.y=-x+3
7.小聪在画一次函数时,当他列表后,发现题中一次函数y=◆x+◆中的k和b看不清了,则( )
x 0 3
y 2 0
A.k=2,b=3 B.k=-,b=2 C.k=3,b=2 D.k=1,b=-1
易错点 考虑问题不全面导致丢解
8.已知直线y=-2x-b与y轴的交点到原点的距离为5,则直线y=-2x-b对应的函数表达式为______________________。
能力提升
9.若一个正比例函数的图象经过A(3,-6),B(m,-4)两点,则m的值为( )
A.2 B.8 C.-2 D.-8
10.已知正比例函数y=kx(k≠0)的图象如图所示,则在下列选项中k值可能是( )
A.1 B.2 C.3 D.4
11.如图,直线AB对应的函数表达式是( )
A.y=-x+3 B.y=x+3 C.y=-x+3 D.y=x+3
12.将直线y=x+b沿y轴向下平移3个单位长度,点A(-1,2)关于y轴的对称点落在平移后的直线上,则b的值为( )
A.-3 B.3 C.4 D.-4
13.已知一次函数y=kx+b(k≠0)的图象过点(0,2),且与两坐标轴围成的三角形面积为2,则一次函数的表达式为( )
A.y=x+2 B.y=-x+2 C.y=x+2或y=-x+2 D.y=-x+2或y=x-2
14.不论m取何值,如果点P(2m,m+1)都在某一条直线上,则这条直线的表达式是( )
A.y=2x-1 B.y=2x+1 C.y=x-1 D.y=x+1
15.请根据以下信息写出函数的表达式:__________________。
①它的图象是不经过第二象限的一条直线,且与y轴的交点P到原点O的距离为3;②当x为2时,函数y的值就为0.
16.一次函数y=kx+b,当0≤x≤2,0≤y≤3时,则 kb=______________。
17.已知一次函数的图象经过点(0,1),且与x,y轴围成的三角形的面积为3,则该一次函数的表达式为_______________________。
18.如图,将含45°角的直角三角尺放置在平面直角坐标系中,其中A(-2,0),B(0,1),求直线BC的函数表达式。
素养提升
19.已知点A1(a1,a2),A2(a2,a3),A3(a3,a4),…,An(an,an+1)(n为正整数)都在一次函数y=x+3的图象上.若a1=2,则试探究a2020的值。
20.如图,直线AB与x轴,y轴的交点分别为A,B两点,点A的纵坐标,点B的横坐标如图所示.
(1)求直线AB的表达式及△AOB的面积;
(2)在x轴上是否存在一点P,使S△PAB=3?若存在,求出点P的坐标;若不存在,说明理由。
参考答案
1.A 2.B
3.解:(1)根据题意,设y=k·2x,当x=3,y=-12时,有-12=k·2×3,解得k=-2。所以y与x之间的函数表达式为y=-4x。
(2)把x=5代入函数表达式,得y=-4×5=-20.
4.A 5.C 6.D 7.B 8.y=-2x+5或y=-2x-5
9.A 10.B 11.A 12.C 13.C 14.D
15. 16.0或- 17.或
18.解:如图,过点C作CD⊥x轴于点D。因为∠CAB=90°,所以∠DAC+∠BAO=∠BAO+∠ABO=90° 。所以∠DAC=∠ABO.
在△AOB和△CDA中,∠ABO=∠CAD,∠AOB=∠CDA,AB=AC,
所以△AOB≌△CDA(AAS)。
因为A(-2,0),B(0,1),所以AD=BO=1,CD=AO=2,
所以点C的坐标为(-3,2).
设直线BC的函数表达式为y=kx+b,则有-3k+b=2,b=1,解得k=-。
所以直线BC的函数表达式为y=-x+1.
19.解:将a1=2代入a2=x+3,得a2=5.
同理,得a3=8,a4=11,a5=14,…,an=2+3(n-1),
故a2020=2+3×(2020-1)=2+3×2019=6059.
20.解:设直线AB的表达式为y=kx+2.把B(4,0)代入,得4k+2=0,解得k=-。
所以直线AB的表达式为y=-x+2.所以S△AOB=OA·OB=×2×4=4.
(2)在x轴上存在一点P,使S△PAB=3,理由
如图,当BP=3时,则S△PAB=3,此时点P的坐标为(7,0)。
当BP'=3时,则S△P'AB=3,此时点P'的坐标为(1,0)。
综上所述,符合题意的点P的坐标为(1,0),(7,0)。
_21?????????è?????(www.21cnjy.com)_
第六章 一次函数
4 确定一次函数的表达式
夯实基础
知识点一 求正比例函数的表达式
1.已知y与x成正比例,且x=3时,y=2,则y=3时,x的值为( )
A. B. C.2 D.12
2.如图,直线所表示的变量x,y之间的函数关系式为( )
A.y=-2x B.y=2x C.y=-x D.y=x
3.已知y与2x成正比例,且当x=3时,y=-12.
(1)求y与x之间的函数表达式;
(2)求当x=5时y的值.
知识点二 求一次函数的表达式
4.已知直线经过点A(4,0),B(0,3),则直线的函数表达式为( )
A.y=-x+3 B.y=3x+4 C.y=4x+3 D.y=-3x+3
5.已知y是x的一次函数,下表中列出了部分对应值,则m等于( )
x -1 0 1
y 1 -2 m
A.-1 B.0 C.-5 D.
6.如图,过点A的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的表达式是( )
A.y=2x+3 B.y=x-3 C.y=2x-3 D.y=-x+3
7.小聪在画一次函数时,当他列表后,发现题中一次函数y=◆x+◆中的k和b看不清了,则( )
x 0 3
y 2 0
A.k=2,b=3 B.k=-,b=2 C.k=3,b=2 D.k=1,b=-1
易错点 考虑问题不全面导致丢解
8.已知直线y=-2x-b与y轴的交点到原点的距离为5,则直线y=-2x-b对应的函数表达式为______________________。
能力提升
9.若一个正比例函数的图象经过A(3,-6),B(m,-4)两点,则m的值为( )
A.2 B.8 C.-2 D.-8
10.已知正比例函数y=kx(k≠0)的图象如图所示,则在下列选项中k值可能是( )
A.1 B.2 C.3 D.4
11.如图,直线AB对应的函数表达式是( )
A.y=-x+3 B.y=x+3 C.y=-x+3 D.y=x+3
12.将直线y=x+b沿y轴向下平移3个单位长度,点A(-1,2)关于y轴的对称点落在平移后的直线上,则b的值为( )
A.-3 B.3 C.4 D.-4
13.已知一次函数y=kx+b(k≠0)的图象过点(0,2),且与两坐标轴围成的三角形面积为2,则一次函数的表达式为( )
A.y=x+2 B.y=-x+2 C.y=x+2或y=-x+2 D.y=-x+2或y=x-2
14.不论m取何值,如果点P(2m,m+1)都在某一条直线上,则这条直线的表达式是( )
A.y=2x-1 B.y=2x+1 C.y=x-1 D.y=x+1
15.请根据以下信息写出函数的表达式:__________________。
①它的图象是不经过第二象限的一条直线,且与y轴的交点P到原点O的距离为3;②当x为2时,函数y的值就为0.
16.一次函数y=kx+b,当0≤x≤2,0≤y≤3时,则 kb=______________。
17.已知一次函数的图象经过点(0,1),且与x,y轴围成的三角形的面积为3,则该一次函数的表达式为_______________________。
18.如图,将含45°角的直角三角尺放置在平面直角坐标系中,其中A(-2,0),B(0,1),求直线BC的函数表达式。
素养提升
19.已知点A1(a1,a2),A2(a2,a3),A3(a3,a4),…,An(an,an+1)(n为正整数)都在一次函数y=x+3的图象上.若a1=2,则试探究a2020的值。
20.如图,直线AB与x轴,y轴的交点分别为A,B两点,点A的纵坐标,点B的横坐标如图所示.
(1)求直线AB的表达式及△AOB的面积;
(2)在x轴上是否存在一点P,使S△PAB=3?若存在,求出点P的坐标;若不存在,说明理由。
参考答案
1.A 2.B
3.解:(1)根据题意,设y=k·2x,当x=3,y=-12时,有-12=k·2×3,解得k=-2。所以y与x之间的函数表达式为y=-4x。
(2)把x=5代入函数表达式,得y=-4×5=-20.
4.A 5.C 6.D 7.B 8.y=-2x+5或y=-2x-5
9.A 10.B 11.A 12.C 13.C 14.D
15. 16.0或- 17.或
18.解:如图,过点C作CD⊥x轴于点D。因为∠CAB=90°,所以∠DAC+∠BAO=∠BAO+∠ABO=90° 。所以∠DAC=∠ABO.
在△AOB和△CDA中,∠ABO=∠CAD,∠AOB=∠CDA,AB=AC,
所以△AOB≌△CDA(AAS)。
因为A(-2,0),B(0,1),所以AD=BO=1,CD=AO=2,
所以点C的坐标为(-3,2).
设直线BC的函数表达式为y=kx+b,则有-3k+b=2,b=1,解得k=-。
所以直线BC的函数表达式为y=-x+1.
19.解:将a1=2代入a2=x+3,得a2=5.
同理,得a3=8,a4=11,a5=14,…,an=2+3(n-1),
故a2020=2+3×(2020-1)=2+3×2019=6059.
20.解:设直线AB的表达式为y=kx+2.把B(4,0)代入,得4k+2=0,解得k=-。
所以直线AB的表达式为y=-x+2.所以S△AOB=OA·OB=×2×4=4.
(2)在x轴上存在一点P,使S△PAB=3,理由
如图,当BP=3时,则S△PAB=3,此时点P的坐标为(7,0)。
当BP'=3时,则S△P'AB=3,此时点P'的坐标为(1,0)。
综上所述,符合题意的点P的坐标为(1,0),(7,0)。
_21?????????è?????(www.21cnjy.com)_
