高中数学人教A版必修1第三章3.1.1 方程的根与函数的零点课件(23张PPT)
文档属性
| 名称 | 高中数学人教A版必修1第三章3.1.1 方程的根与函数的零点课件(23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 20:50:22 | ||
图片预览







文档简介
函数的零点和二分法
函数的零点定义:
方程f(x)=0的根就是函数y=f(x)的零点。
函数与方程的关系:
(1)方程f(x)=0的根就是函数y=f(x)的图像与x轴交点的横坐标。
(2)方程f(x)=g(x)的根就是函数y=f(x)的图像与y=g(x)的图像交点的横坐标。
根据函数与方程的关系:
(1)方程f(x)=0有几个根?函数y=f(x)的图像与x轴有几个交点。
(2)方程f(x)=g(x)有几个根?函数y=f(x)的图像与y=g(x)的图像有几个交点。
(3)求解方程f(x)=0、f(x)=g(x)的根,或估计根的范围,或判断根的个数,均可通过图像来求解。
根的存在性定理:
根的存在性定理:
若①y=f(x)在[a,b]上连续,②f(a)f(b)<0,
则f(x)=0在(a,b)内存在实根。
推论:
若①y=f(x)在[a,b]上连续,②f(a)f(b)<0,
③y=f(x)在[a,b]上单调,
则f(x)=0在(a,b)内存在唯一实根。
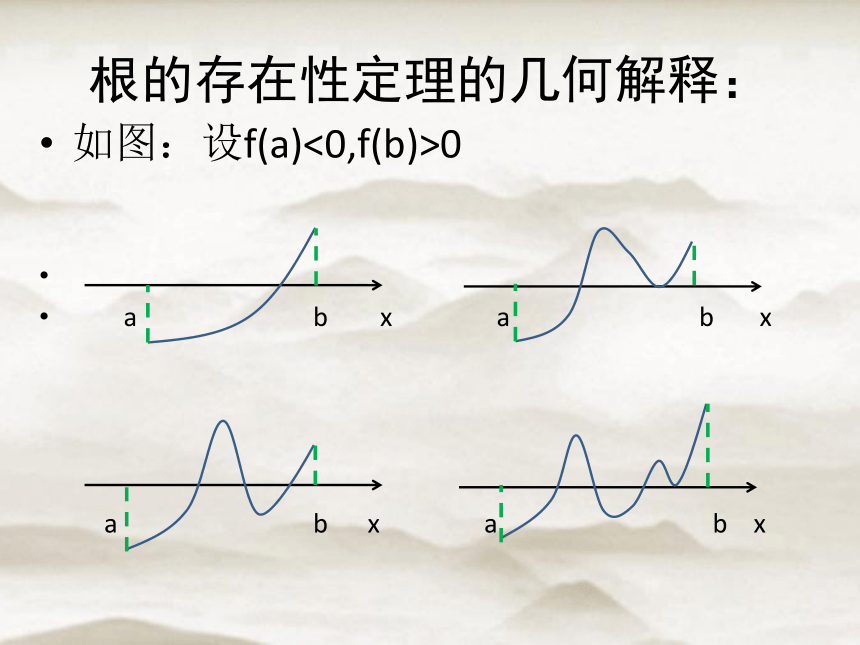
根的存在性定理的几何解释:
如图:设f(a)<0,f(b)>0
a b x a b x
a b x a b x
例1.f????=2????????????????0.5?????1的零点的个数为( )
A、1 B、2 C、3 D、4
?
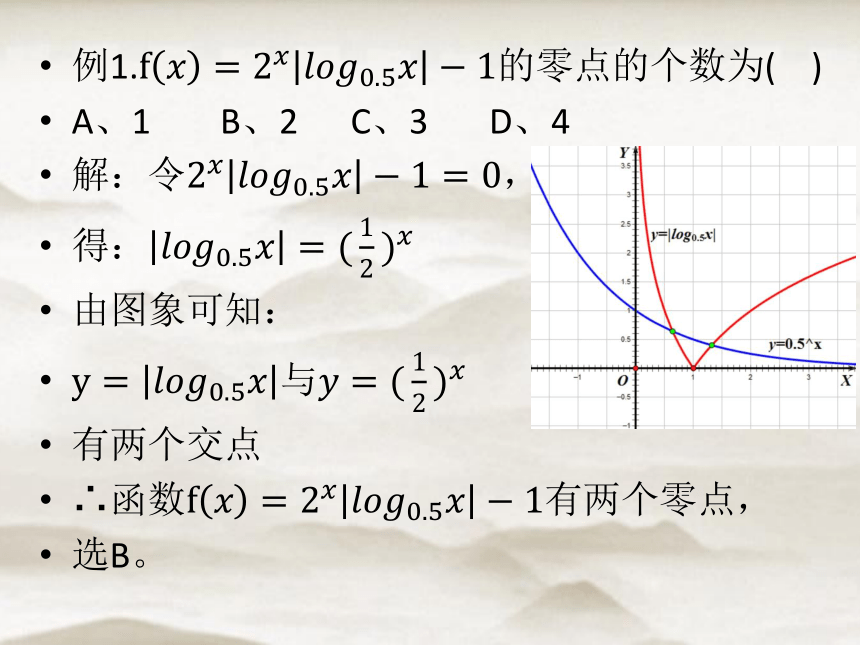
例1.f????=2????????????????0.5?????1的零点的个数为( )
A、1 B、2 C、3 D、4
解:令2????????????????0.5?????1=0,
得:????????????0.5????=(12)????
由图象可知:
y=????????????0.5????与????=(12)????
有两个交点
∴函数f????=2????????????????0.5?????1有两个零点,
选B。
?
例2.设f????=2????+????3?2的零点所在的区间为n,n+1,n∈Z,则n= 。
?
例2.设f????=2????+????3?2的零点所在的区间为n,n+1,n∈Z,则n= 。
?
例2.设f????=2????+????3?2的零点所在的区间为n,n+1,n∈Z,则n= 。
解:令2????+????3?2=0得:2?????2=?????3
由图象可知:y=2?????2与????=?????3的交点横坐标的区间估计为(0,1)
∴f????=2????+????3?2的零点所在的区间估计为0,1
验证:∵f0=?1<0,f1=1>0
∴f0f1<0
∴零点所在的区间为0,1
∴n=0
?
例2.设f????=2????+????3?2的零点所在的区间为n,n+1,n∈Z,则n= 。
练:若aA、(a,b)和(b,c) B、(-∞,a)和(a,b)
C、(b,c)和(c,+∞) D、(-∞,a)和(c,+∞)
?
例2.设f????=2????+????3?2的零点所在的区间为n,n+1,n∈Z,则n= 。
练:若aA、(a,b)和(b,c) B、(-∞,a)和(a,b)
C、(b,c)和(c,+∞) D、(-∞,a)和(c,+∞)
解:∵f????=a?ba?c>0,
f????=b?ab?c<0,
f????=c?ac?b>0
∴两个零点所在的区间分别为(a,b)和(b,c)。
?
a
b
x
二分法的几何解释
????1
?
????2
?
????1
?
????2
?
????3
?
y=f(x)
用二分法解方程f(x)=0(求函数y=f(x)零点)的步骤:
(1)确定初始区间(a,b),检验f(a)f(b)<0,给出精度ε;
(2)计算m=????+????2;
(3)计算f(m):
①若f(m)=0,则ξ=m;
②若f(a)f(m)<0,则ξ∈(a,m),令a=a,b=m;
③若f(m)f(b)<0,则ξ∈(m,b),令a=m,b=b;
(4)判断是否达到精度ε:
①若????????? ②若?????????≥????,则未达到精度,重复步骤
(2)(3)(4) ,直到??????????
开始
定义f(x)
输入a,b,ε
m=(a+b)/2
|a-b|<ε
f(m)=0
结束
二分法程序框图
f(a)f(m)<0
否
输出x=m为根
是
b=m
是
a=m
否
否
m=(a+b)/2
是
例3、估计函数f(x)=lnx+2x-6零点.
解:方程lnx+2x-6=0等价于方程lnx=6-2x。
下面考查y=lnx与y=6-2x图像间的关系。
第一步:画出函数图像,找到根存在的大致区间。
由图像知:
方程lnx=6-2x恰有一个根,此根在区间(2,3)内。
因为f(2)=ln2-2lne=1>0
所以f(2)f(3)<0…………………………………………………..条件1
又f(x)=lnx+2x-6在区间[2,3]内连续………………..…条件2
所以lnx+2x-6=0在区间(2,3)内存在实根。……...结论1
又因为f(x)=lnx+2x-6在区间[2,3]内单调递增…..条件3
所以lnx+2x-6=0在区间(2,3)内存在唯一实根。结论2
第二步:利用根的存在性定理及其推论,说明根存在与上述区间内。
下面用人工方法——放缩法,
来缩小根存在的区间。
第一步:初始区间确定
∵f2=ln2?2 f(3)=ln3>lne=1>0
∴f2f3<0
∴????0∈2,3,区间长度为1
?
下面用人工方法——放缩法,
来缩小根存在的区间。
第二步:第一次二分
∵f52=ln52?1∴f52f3<0
∴????0∈52,3,区间长度为1?2;
?
下面用人工方法——放缩法,
来缩小根存在的区间。
第三步:第二次二分
∵f114=ln114?12=ln2.75?12
>ln?????12=12>0
∴f52f114<0
∴????0∈52,114,区间长度为14
?
第四步:第三次二分
f218=ln218?34=ln218?ln????34
=12ln44164?ln????3
∵????3<(114)3=133164<136964=(378)2
∴????3<378=29664<44164
?ln44164?ln????3>0
∴f218>0
∴????0∈52,218,区间长度为18.
?
数与形,本是相依倚,
焉能分作两边飞,
数缺形时少直觉,
形少数时难入微,
形数结合百般好,
割裂分家万事休,
切莫忘,几何代数流一体,
永远联系切莫分离。
——华罗庚
下面用二分法,结合计算机程序,来求解方程lnx+2x-6=0的近似解。
函数的零点定义:
方程f(x)=0的根就是函数y=f(x)的零点。
函数与方程的关系:
(1)方程f(x)=0的根就是函数y=f(x)的图像与x轴交点的横坐标。
(2)方程f(x)=g(x)的根就是函数y=f(x)的图像与y=g(x)的图像交点的横坐标。
根据函数与方程的关系:
(1)方程f(x)=0有几个根?函数y=f(x)的图像与x轴有几个交点。
(2)方程f(x)=g(x)有几个根?函数y=f(x)的图像与y=g(x)的图像有几个交点。
(3)求解方程f(x)=0、f(x)=g(x)的根,或估计根的范围,或判断根的个数,均可通过图像来求解。
根的存在性定理:
根的存在性定理:
若①y=f(x)在[a,b]上连续,②f(a)f(b)<0,
则f(x)=0在(a,b)内存在实根。
推论:
若①y=f(x)在[a,b]上连续,②f(a)f(b)<0,
③y=f(x)在[a,b]上单调,
则f(x)=0在(a,b)内存在唯一实根。
根的存在性定理的几何解释:
如图:设f(a)<0,f(b)>0
a b x a b x
a b x a b x
例1.f????=2????????????????0.5?????1的零点的个数为( )
A、1 B、2 C、3 D、4
?
例1.f????=2????????????????0.5?????1的零点的个数为( )
A、1 B、2 C、3 D、4
解:令2????????????????0.5?????1=0,
得:????????????0.5????=(12)????
由图象可知:
y=????????????0.5????与????=(12)????
有两个交点
∴函数f????=2????????????????0.5?????1有两个零点,
选B。
?
例2.设f????=2????+????3?2的零点所在的区间为n,n+1,n∈Z,则n= 。
?
例2.设f????=2????+????3?2的零点所在的区间为n,n+1,n∈Z,则n= 。
?
例2.设f????=2????+????3?2的零点所在的区间为n,n+1,n∈Z,则n= 。
解:令2????+????3?2=0得:2?????2=?????3
由图象可知:y=2?????2与????=?????3的交点横坐标的区间估计为(0,1)
∴f????=2????+????3?2的零点所在的区间估计为0,1
验证:∵f0=?1<0,f1=1>0
∴f0f1<0
∴零点所在的区间为0,1
∴n=0
?
例2.设f????=2????+????3?2的零点所在的区间为n,n+1,n∈Z,则n= 。
练:若a
C、(b,c)和(c,+∞) D、(-∞,a)和(c,+∞)
?
例2.设f????=2????+????3?2的零点所在的区间为n,n+1,n∈Z,则n= 。
练:若a
C、(b,c)和(c,+∞) D、(-∞,a)和(c,+∞)
解:∵f????=a?ba?c>0,
f????=b?ab?c<0,
f????=c?ac?b>0
∴两个零点所在的区间分别为(a,b)和(b,c)。
?
a
b
x
二分法的几何解释
????1
?
????2
?
????1
?
????2
?
????3
?
y=f(x)
用二分法解方程f(x)=0(求函数y=f(x)零点)的步骤:
(1)确定初始区间(a,b),检验f(a)f(b)<0,给出精度ε;
(2)计算m=????+????2;
(3)计算f(m):
①若f(m)=0,则ξ=m;
②若f(a)f(m)<0,则ξ∈(a,m),令a=a,b=m;
③若f(m)f(b)<0,则ξ∈(m,b),令a=m,b=b;
(4)判断是否达到精度ε:
①若????????? ②若?????????≥????,则未达到精度,重复步骤
(2)(3)(4) ,直到??????????
开始
定义f(x)
输入a,b,ε
m=(a+b)/2
|a-b|<ε
f(m)=0
结束
二分法程序框图
f(a)f(m)<0
否
输出x=m为根
是
b=m
是
a=m
否
否
m=(a+b)/2
是
例3、估计函数f(x)=lnx+2x-6零点.
解:方程lnx+2x-6=0等价于方程lnx=6-2x。
下面考查y=lnx与y=6-2x图像间的关系。
第一步:画出函数图像,找到根存在的大致区间。
由图像知:
方程lnx=6-2x恰有一个根,此根在区间(2,3)内。
因为f(2)=ln2-2
所以f(2)f(3)<0…………………………………………………..条件1
又f(x)=lnx+2x-6在区间[2,3]内连续………………..…条件2
所以lnx+2x-6=0在区间(2,3)内存在实根。……...结论1
又因为f(x)=lnx+2x-6在区间[2,3]内单调递增…..条件3
所以lnx+2x-6=0在区间(2,3)内存在唯一实根。结论2
第二步:利用根的存在性定理及其推论,说明根存在与上述区间内。
下面用人工方法——放缩法,
来缩小根存在的区间。
第一步:初始区间确定
∵f2=ln2?2
∴f2f3<0
∴????0∈2,3,区间长度为1
?
下面用人工方法——放缩法,
来缩小根存在的区间。
第二步:第一次二分
∵f52=ln52?1
∴????0∈52,3,区间长度为1?2;
?
下面用人工方法——放缩法,
来缩小根存在的区间。
第三步:第二次二分
∵f114=ln114?12=ln2.75?12
>ln?????12=12>0
∴f52f114<0
∴????0∈52,114,区间长度为14
?
第四步:第三次二分
f218=ln218?34=ln218?ln????34
=12ln44164?ln????3
∵????3<(114)3=133164<136964=(378)2
∴????3<378=29664<44164
?ln44164?ln????3>0
∴f218>0
∴????0∈52,218,区间长度为18.
?
数与形,本是相依倚,
焉能分作两边飞,
数缺形时少直觉,
形少数时难入微,
形数结合百般好,
割裂分家万事休,
切莫忘,几何代数流一体,
永远联系切莫分离。
——华罗庚
下面用二分法,结合计算机程序,来求解方程lnx+2x-6=0的近似解。
