高中数学人教A版必修1第一章2.1.2指数函数及其性质公开课课件(21张PPT)
文档属性
| 名称 | 高中数学人教A版必修1第一章2.1.2指数函数及其性质公开课课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 481.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 21:23:49 | ||
图片预览







文档简介
铜梁中学数学组
罗术群
指数函数及其性质
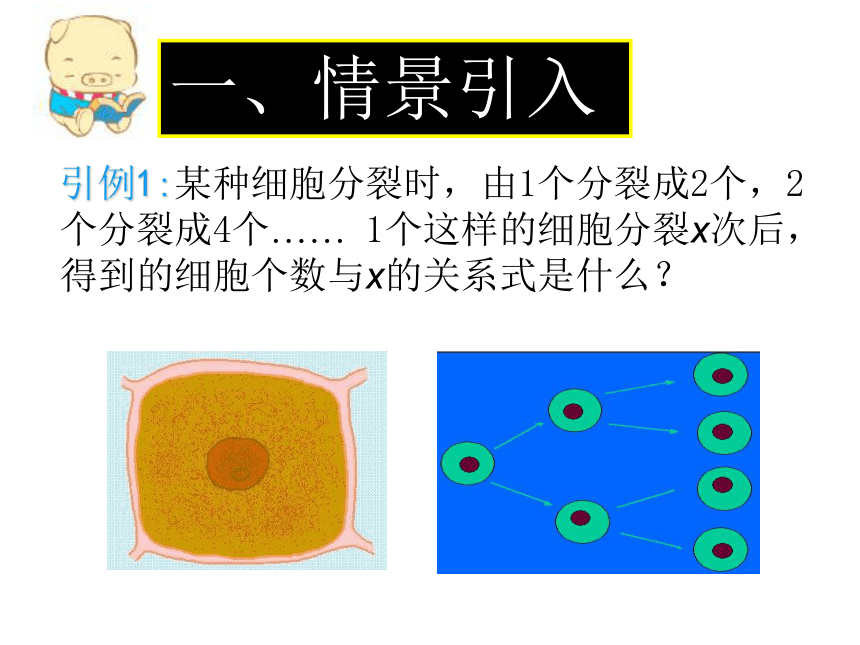
引例1:某种细胞分裂时,由1个分裂成2个,2个分裂成4个…… 1个这样的细胞分裂x次后,得到的细胞个数与x的关系式是什么?
一、情景引入
分裂
次数
细胞
总数
1次
2次
3次
4次
x次
……
21
22
23
24
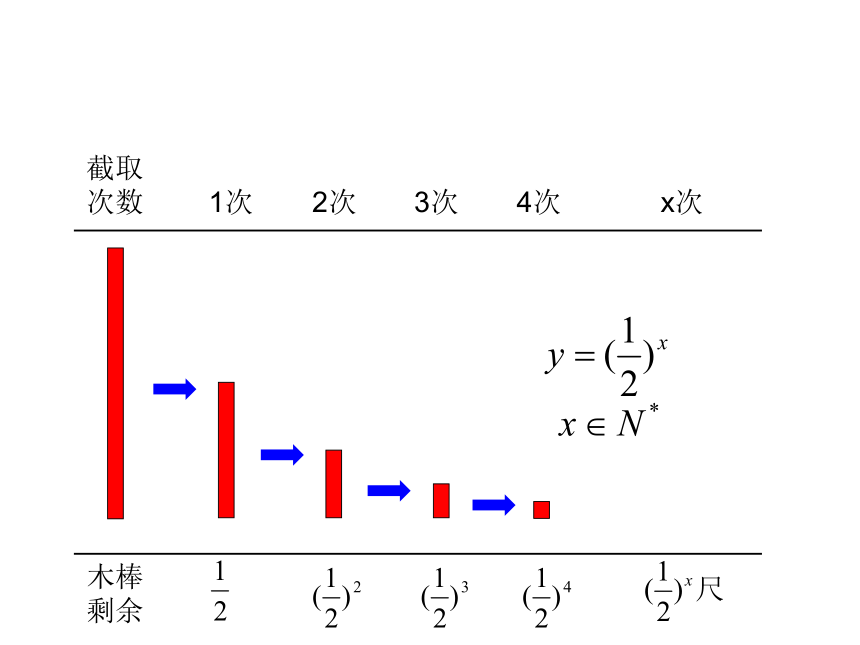
引例2:
“一尺之锤,日取其半,万世不竭”出自《庄子》
长度为1的尺子第一次截去它的一半,第二次截
去剩余部分的一半,第三次截去第二次剩余部分的一半,依次截下去,问截的次数与剩下的尺子长度之间的关系.
截取
次数
木棒
剩余
1次
2次
3次
4次
x次
1.这两个解析式是否构成函数?
思考:
2.两解析式是否具有
的形式?
是
是
其中:自变量
是指数,
大于
底数
且不等于
的常量.
是一个
1.指数函数的定义:
一般地,函数y=ax (a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R。
自变量为x
系数为1
y=1 · ax
a是常数(a>0,且a≠1)
二、探求新知
问题1:为何规定a>0且a≠1?
对于x取某些数值,是不一定有意义.
当
时,
在
处无意义.
当
时,
当
时,
无研究价值.
当
时,
无意义.
当
时,
无研究价值.
如:
随堂练习:下列函数中,哪些是指数函数?
我是
我还不是哟
我不是
我也不是
你答对了吗?
总结:指数函数严格限定
这一结构,稍微有点出入,就会导致非指数函数的出现。
(1)有些看起来是指数函数,而实际上不是指数函数;
(2)有些看起来不是指数函数,而实际上是指数函数.
如:
如:
问题2:已知函数的解析式,得到函数的图象一般用什么方法?
列表
描点
连线成图
y
x
0
y= 2x
y = x
1 2 3 4 5 6 7 8
8
7
6
5
4
3
2
1
-3 -2 -1
-1
-2
-3
y = 2x
x
-1
0
1
2
3
y
8
4
2
1
0.5
8
4
2
1
0.5
x
-3
-2
-1
0
1
y
y = x
2.函数的图像
0
1
2
3
-1
-2
-3
1
2
y=2x
两个函数图象关于y轴对称
问题3:函数
的图象与函数
的图像
有什么关系?可否利用
的图象画出
的图象?
0
1
1
函数y=f(x)与y=f(-x)的函数图象
关于y轴对称
(2)函数 的图像与函数 的图像关于y轴对称.
小结:(1)函数 的图像与函数 的图
像关于y轴对称.
思考4:指数函数的图像有哪些共同特征?
(几何画板演示)
(1)图像是否左右无限延伸?
(2)图像是在X轴上方,还是下方?
(3)图像过定点______________
(4)在第一象限,底数越大,图像越________,
在第二象限,底数越大,图像越________;
(5)当0 当a>1时,函数单调递________.
是
上方
高
低
减
增
y=ax
a>1
0图象
定义域
值域
定点
奇偶性
单调性
函数值
分布
y
y=1
O
x
(0,1)
y=1
(0,1)
x
O
y
R
(0, +∞)
都过定点(0,1)
非奇非偶函数
在R上是增函数
在R上是减函数
若x>0, 则y>1
若x<0, 则0若x>0, 则0若x<0, 则y>1
3.函数的图像和性质
例题1、已知指数函数 的图像经过
点(3,π)求 , , 的值。
解:因为
的图像过点
所以
即
解得
于是
所以,
三、 典例分析、巩固训练
例题2、比较下列各题中两个值的大小:
(1) 1.72.5,1.73;
(2) 0.8-0.1,0.8-0.2;
(3) 1.70.3,0.93.1.
解:(1) 1.72.5 1.73;
(2) 0.8-0.1 0.8-0.2;
(3) 1.70.3 0.93.1.
课堂练习:
四、归纳小结
(1) 通过本节课的学习,你学到了哪些知识?
(2) 你学会了哪些数学思想方法?
1.指数函数的定义以及指数函数的一般表达式的特征;
2.指数函数的图像及其简图的画法;
3.指数函数的性质.
1.数形结合思想;
2.分类讨论思想;
3.从具体到一般的抽象概括的方法 .
罗术群
指数函数及其性质
引例1:某种细胞分裂时,由1个分裂成2个,2个分裂成4个…… 1个这样的细胞分裂x次后,得到的细胞个数与x的关系式是什么?
一、情景引入
分裂
次数
细胞
总数
1次
2次
3次
4次
x次
……
21
22
23
24
引例2:
“一尺之锤,日取其半,万世不竭”出自《庄子》
长度为1的尺子第一次截去它的一半,第二次截
去剩余部分的一半,第三次截去第二次剩余部分的一半,依次截下去,问截的次数与剩下的尺子长度之间的关系.
截取
次数
木棒
剩余
1次
2次
3次
4次
x次
1.这两个解析式是否构成函数?
思考:
2.两解析式是否具有
的形式?
是
是
其中:自变量
是指数,
大于
底数
且不等于
的常量.
是一个
1.指数函数的定义:
一般地,函数y=ax (a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R。
自变量为x
系数为1
y=1 · ax
a是常数(a>0,且a≠1)
二、探求新知
问题1:为何规定a>0且a≠1?
对于x取某些数值,是不一定有意义.
当
时,
在
处无意义.
当
时,
当
时,
无研究价值.
当
时,
无意义.
当
时,
无研究价值.
如:
随堂练习:下列函数中,哪些是指数函数?
我是
我还不是哟
我不是
我也不是
你答对了吗?
总结:指数函数严格限定
这一结构,稍微有点出入,就会导致非指数函数的出现。
(1)有些看起来是指数函数,而实际上不是指数函数;
(2)有些看起来不是指数函数,而实际上是指数函数.
如:
如:
问题2:已知函数的解析式,得到函数的图象一般用什么方法?
列表
描点
连线成图
y
x
0
y= 2x
y = x
1 2 3 4 5 6 7 8
8
7
6
5
4
3
2
1
-3 -2 -1
-1
-2
-3
y = 2x
x
-1
0
1
2
3
y
8
4
2
1
0.5
8
4
2
1
0.5
x
-3
-2
-1
0
1
y
y = x
2.函数的图像
0
1
2
3
-1
-2
-3
1
2
y=2x
两个函数图象关于y轴对称
问题3:函数
的图象与函数
的图像
有什么关系?可否利用
的图象画出
的图象?
0
1
1
函数y=f(x)与y=f(-x)的函数图象
关于y轴对称
(2)函数 的图像与函数 的图像关于y轴对称.
小结:(1)函数 的图像与函数 的图
像关于y轴对称.
思考4:指数函数的图像有哪些共同特征?
(几何画板演示)
(1)图像是否左右无限延伸?
(2)图像是在X轴上方,还是下方?
(3)图像过定点______________
(4)在第一象限,底数越大,图像越________,
在第二象限,底数越大,图像越________;
(5)当0
是
上方
高
低
减
增
y=ax
a>1
0
定义域
值域
定点
奇偶性
单调性
函数值
分布
y
y=1
O
x
(0,1)
y=1
(0,1)
x
O
y
R
(0, +∞)
都过定点(0,1)
非奇非偶函数
在R上是增函数
在R上是减函数
若x>0, 则y>1
若x<0, 则0
3.函数的图像和性质
例题1、已知指数函数 的图像经过
点(3,π)求 , , 的值。
解:因为
的图像过点
所以
即
解得
于是
所以,
三、 典例分析、巩固训练
例题2、比较下列各题中两个值的大小:
(1) 1.72.5,1.73;
(2) 0.8-0.1,0.8-0.2;
(3) 1.70.3,0.93.1.
解:(1) 1.72.5 1.73;
(2) 0.8-0.1 0.8-0.2;
(3) 1.70.3 0.93.1.
课堂练习:
四、归纳小结
(1) 通过本节课的学习,你学到了哪些知识?
(2) 你学会了哪些数学思想方法?
1.指数函数的定义以及指数函数的一般表达式的特征;
2.指数函数的图像及其简图的画法;
3.指数函数的性质.
1.数形结合思想;
2.分类讨论思想;
3.从具体到一般的抽象概括的方法 .
