高中数学人教A版必修2第二章2.2.3 直线与平面平行的性质 课件(21张PPT)
文档属性
| 名称 | 高中数学人教A版必修2第二章2.2.3 直线与平面平行的性质 课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 227.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 20:58:07 | ||
图片预览






文档简介
直线与平面平行的性质
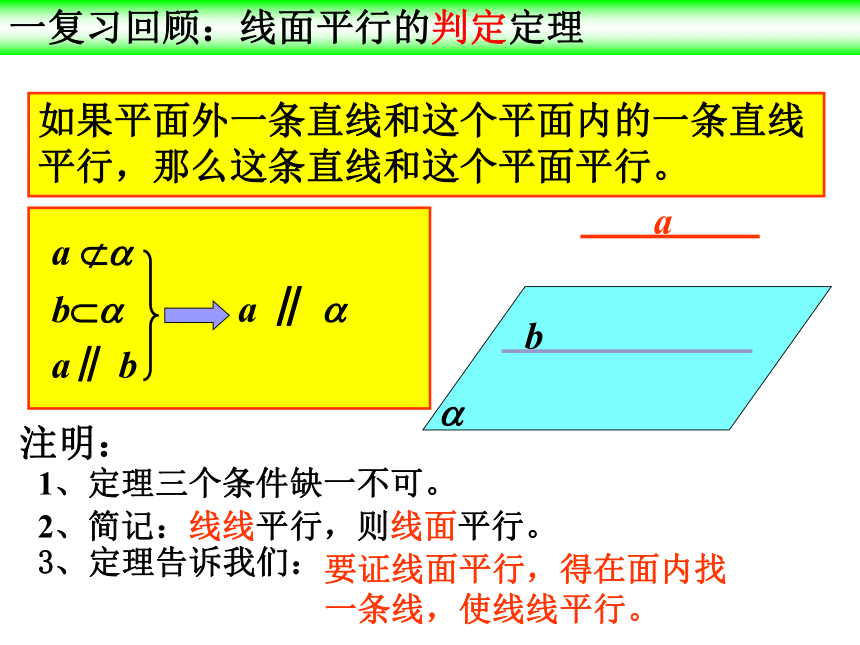
一复习回顾:线面平行的判定定理
如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
?
b
a
b??
a∥ b
a ??
a ∥ ?
注明:
1、定理三个条件缺一不可。
2、简记:线线平行,则线面平行。
3、定理告诉我们:
要证线面平行,得在面内找一条线,使线线平行。
如果一条直线与一个平面 平行,那么这条直线与这个平面内的直线有哪些位置关系?
a
b
有平行,
但不会相交
?
有异面
二、思考与探究
在怎样的条件下,平面?内的直线与直线a平行呢?
a
?
∵ a与平面?内的任何直
线都无公共点,
∴过直线a的某一个平面
?,若与平面?相交,
则直线a就平行于这一条交线
思考出新知
?
b
a
?
?
?
证明:
结论证明
?
?
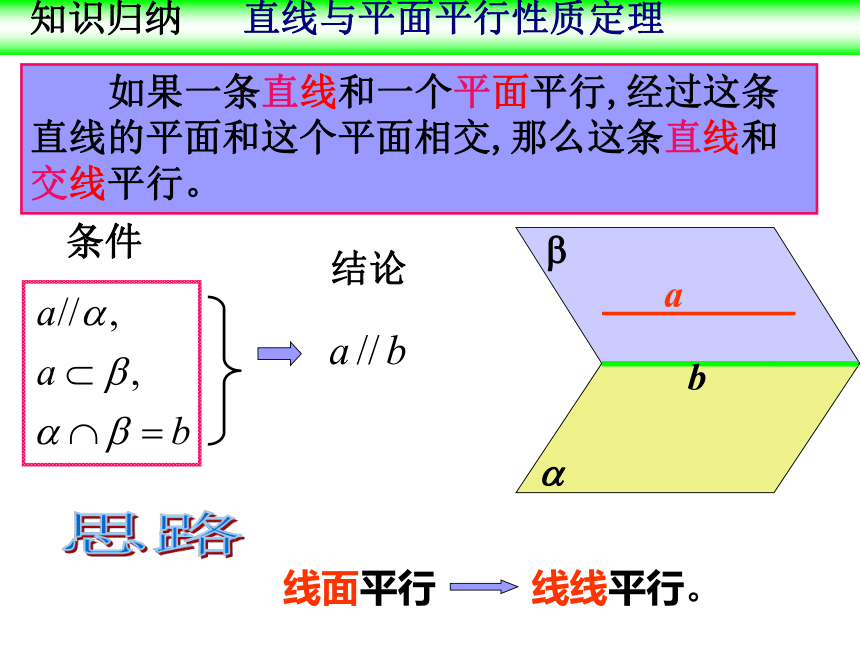
知识归纳
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
b
a
直线与平面平行性质定理
条件
结论
思路
线面平行 线线平行。
三练习巩固
1.已知直线a//平面?,P? ? ,那么过点P且平
行于直线a的直线___
A)只有一条,不在平面?内
B)有无数条,不一定在?内
C)只有一条,且在平面?内
D)有无数条,一定有?内
2.能保证a// ?的条件是
教室内的日光灯管所在的直线与地面平行,如何在地面上作一条直线与灯管所在的直线平行?
定理活用1
从灯管上任意两点向地面作铅垂线,过垂线与地面的交点的直线就是与灯管所在的直线平行的直线。
参考方案:
分析
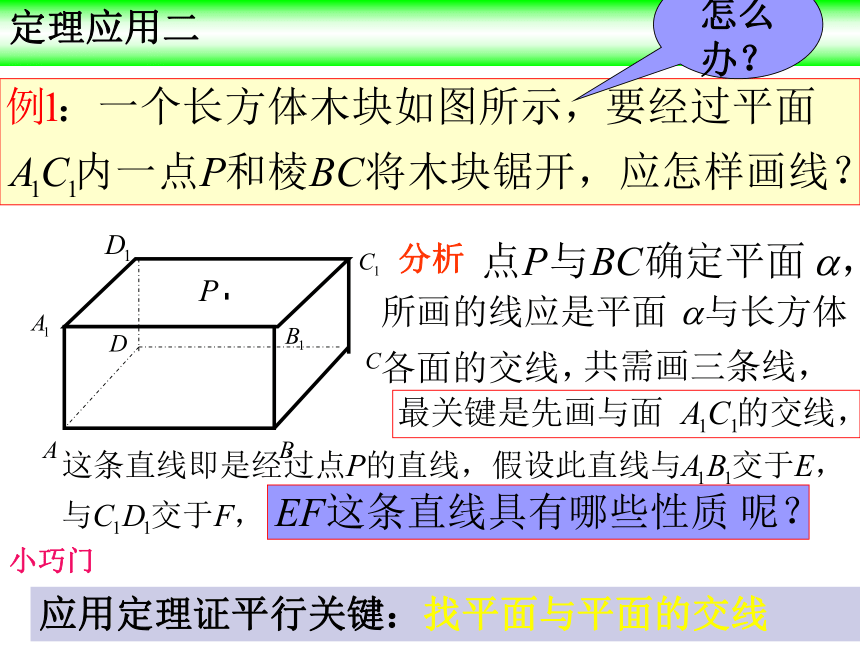
定理应用二
怎么办?
应用定理证平行关键:找平面与平面的交线
小巧门
例2.已知平面外的两条平行直线中的一条平行于一个平面,则另一条也平行于这个平面
已知:直线a//b,a、b
在平面?外,a// ?
求证:b// ?
分析:
由a// ?,则?内可作一条直线c与a平行
c与a是怎样的位置关系?与b呢?
c
定理应用三
例3:求证:如果三个平面两两相交于三条直线,并且其中两条直线平行,那么第三条直线也和它们平行.
定理应用四
四、拓展与提高
1.以下命题(其中a,b表示直线,?表示平面)
①若a∥b,b??,则a∥?
②若a∥?,b∥?,则a∥b
③若a∥b,b∥?,则a∥?
④若a∥?,b??,则a∥b
其中正确命题的个数是 ( )
(A)0个 (B)1个 (C)2个 (D)3个
2.若直线a//平面?,直线b?? ,则a与的关系为
A)相交
B)平行
C)异面
D)平行或异面
(1)若两直线a、b异面,且 a ∥ ?,则b与?的位置关系可能是_________________
3.填空:
(2)若两直线a、b相交,且a ∥ ?,则b与?的位置关系可能是_________________
b ∥ ? ,b与 ?相交
b//? ,或 b ? ,
或b与?相交
设a,b是异面直线,AB是a,b的公垂线,过AB的中点O作平面α与a,b分别平行,M,N分别是a,b上的任意两点,MN与α交于点P。
求证:P是MN的中点。
4.
A
B
M
N
O
α
P
C
五、小结
线面平行性质定理,它还是一种思想
要证a//?,通过构造过直线 a 的平面?与平面?
相交于直线b,只要证得a // b即可。
线//线
线//面
面//面
(1)平行公理 (2) 中位线
(3)平行线分线段成比例
(4)相似三角形对应边成比例
(5)平行四边形对边平行
六、作业
1.若直线a不平行于平面?,下列结论成立的是
A) ?内的所有直线都与直线异面
B) ?内不存在与a平行的直线
C) ?内的直线都与a相交
D)直线与平面?有公共点
2.下列命题中正确的是
A)如果a、b是两条直线,且a∥b,那么a 平行于经过b的任何平面;
B)如果直线a、b和平面α 满足a ∥ α,b ∥ α,那么a ∥ b
C)如果直线a、b和平面α 满足a ∥ b,a ∥ α,b α, 那么 b ∥ α
D)过平面外一点和这个平面平行的直线只有一条
3.判断下列命题的真假
(1)过直线外一点只能引一条直线与
这条直线平行. ( )
(2)过平面外一点只能引一条直线与
这个平面平行. ( )
(3)若两条直线都和第三条直线垂直,
则这两条直线平行. ( )
(4)若两条直线都和第三条直线平行,
则这两条直线平行. ( )
真
假
真
假
4.如图:AB//?,AC//BD,C??,求证:AC=BD
A
B
C
D
ABCD是平行四边形,P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH。
5.
求证:AP∥GH。
A
B
C
D
P
M
G
H
S是空间四边形ABCD对角线BD上任意一点,E、F分别是AD、CD上的点,且AE:AD=CF:CD,BE与AS交于R,BF与SC交于Q。
求证:EF∥RQ。
A
B
C
D
E
F
R
Q
S
6.
一复习回顾:线面平行的判定定理
如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
?
b
a
b??
a∥ b
a ??
a ∥ ?
注明:
1、定理三个条件缺一不可。
2、简记:线线平行,则线面平行。
3、定理告诉我们:
要证线面平行,得在面内找一条线,使线线平行。
如果一条直线与一个平面 平行,那么这条直线与这个平面内的直线有哪些位置关系?
a
b
有平行,
但不会相交
?
有异面
二、思考与探究
在怎样的条件下,平面?内的直线与直线a平行呢?
a
?
∵ a与平面?内的任何直
线都无公共点,
∴过直线a的某一个平面
?,若与平面?相交,
则直线a就平行于这一条交线
思考出新知
?
b
a
?
?
?
证明:
结论证明
?
?
知识归纳
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
b
a
直线与平面平行性质定理
条件
结论
思路
线面平行 线线平行。
三练习巩固
1.已知直线a//平面?,P? ? ,那么过点P且平
行于直线a的直线___
A)只有一条,不在平面?内
B)有无数条,不一定在?内
C)只有一条,且在平面?内
D)有无数条,一定有?内
2.能保证a// ?的条件是
教室内的日光灯管所在的直线与地面平行,如何在地面上作一条直线与灯管所在的直线平行?
定理活用1
从灯管上任意两点向地面作铅垂线,过垂线与地面的交点的直线就是与灯管所在的直线平行的直线。
参考方案:
分析
定理应用二
怎么办?
应用定理证平行关键:找平面与平面的交线
小巧门
例2.已知平面外的两条平行直线中的一条平行于一个平面,则另一条也平行于这个平面
已知:直线a//b,a、b
在平面?外,a// ?
求证:b// ?
分析:
由a// ?,则?内可作一条直线c与a平行
c与a是怎样的位置关系?与b呢?
c
定理应用三
例3:求证:如果三个平面两两相交于三条直线,并且其中两条直线平行,那么第三条直线也和它们平行.
定理应用四
四、拓展与提高
1.以下命题(其中a,b表示直线,?表示平面)
①若a∥b,b??,则a∥?
②若a∥?,b∥?,则a∥b
③若a∥b,b∥?,则a∥?
④若a∥?,b??,则a∥b
其中正确命题的个数是 ( )
(A)0个 (B)1个 (C)2个 (D)3个
2.若直线a//平面?,直线b?? ,则a与的关系为
A)相交
B)平行
C)异面
D)平行或异面
(1)若两直线a、b异面,且 a ∥ ?,则b与?的位置关系可能是_________________
3.填空:
(2)若两直线a、b相交,且a ∥ ?,则b与?的位置关系可能是_________________
b ∥ ? ,b与 ?相交
b//? ,或 b ? ,
或b与?相交
设a,b是异面直线,AB是a,b的公垂线,过AB的中点O作平面α与a,b分别平行,M,N分别是a,b上的任意两点,MN与α交于点P。
求证:P是MN的中点。
4.
A
B
M
N
O
α
P
C
五、小结
线面平行性质定理,它还是一种思想
要证a//?,通过构造过直线 a 的平面?与平面?
相交于直线b,只要证得a // b即可。
线//线
线//面
面//面
(1)平行公理 (2) 中位线
(3)平行线分线段成比例
(4)相似三角形对应边成比例
(5)平行四边形对边平行
六、作业
1.若直线a不平行于平面?,下列结论成立的是
A) ?内的所有直线都与直线异面
B) ?内不存在与a平行的直线
C) ?内的直线都与a相交
D)直线与平面?有公共点
2.下列命题中正确的是
A)如果a、b是两条直线,且a∥b,那么a 平行于经过b的任何平面;
B)如果直线a、b和平面α 满足a ∥ α,b ∥ α,那么a ∥ b
C)如果直线a、b和平面α 满足a ∥ b,a ∥ α,b α, 那么 b ∥ α
D)过平面外一点和这个平面平行的直线只有一条
3.判断下列命题的真假
(1)过直线外一点只能引一条直线与
这条直线平行. ( )
(2)过平面外一点只能引一条直线与
这个平面平行. ( )
(3)若两条直线都和第三条直线垂直,
则这两条直线平行. ( )
(4)若两条直线都和第三条直线平行,
则这两条直线平行. ( )
真
假
真
假
4.如图:AB//?,AC//BD,C??,求证:AC=BD
A
B
C
D
ABCD是平行四边形,P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH。
5.
求证:AP∥GH。
A
B
C
D
P
M
G
H
S是空间四边形ABCD对角线BD上任意一点,E、F分别是AD、CD上的点,且AE:AD=CF:CD,BE与AS交于R,BF与SC交于Q。
求证:EF∥RQ。
A
B
C
D
E
F
R
Q
S
6.
