高中数学人教A版必修2第二章-2.3.1 直线与平面垂直的判定课件(21张PPT)
文档属性
| 名称 | 高中数学人教A版必修2第二章-2.3.1 直线与平面垂直的判定课件(21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 543.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 20:55:17 | ||
图片预览







文档简介
温故而知新
空间直线与平面有哪几种位置关系?
直线与平面平行
直线与平面相交
直线在平面内
2.3.1直线与平面垂直的判定
自 学 提 示
自学课本第64页的内容,请思考下列问题:
1、直线与平面垂直的定义是什么?
2、怎样画直线与平面垂直?
3、用符号语言怎样表示?
限时:
3
分钟
自学——我理解了
1、定义:如果一条直线和一个平面内的 任意 一条直线都垂直,则称这条直线和这个平面垂直.
2、画法
3、符号语言
大判官
判断下列说法是否正确?
1.如果一条直线垂直于平面内的每一条直线,那么这条直线和这个平面垂直.
2.如果一条直线垂直于平面内的所有直线,那么这条直线和这个平面垂直.
3.如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直.
4.如果直线l⊥平面α,直线m?α,则l⊥m.
判断下列说法是否正确?
1.如果一条直线垂直于平面内的每一条直线,那么这条直线和这个平面垂直.
2.如果一条直线垂直于平面内的所有直线,那么这条直线和这个平面垂直.
3.如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直.
4.如果直线l⊥平面α,直线m?α,则l⊥m.
√
大判官
判断下列说法是否正确?
1.如果一条直线垂直于平面内的每一条直线,那么这条直线和这个平面垂直.
2.如果一条直线垂直于平面内的所有直线,那么这条直线和这个平面垂直.
3.如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直.
4.如果直线l⊥平面α,直线m?α,则l⊥m.
√
√
大判官
判断下列说法是否正确?
1.如果一条直线垂直于平面内的每一条直线,那么这条直线和这个平面垂直.
2.如果一条直线垂直于平面内的所有直线,那么这条直线和这个平面垂直.
3.如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直.
4.如果直线l⊥平面α,直线m?α,则l⊥m.
√
√
×
√
大判官
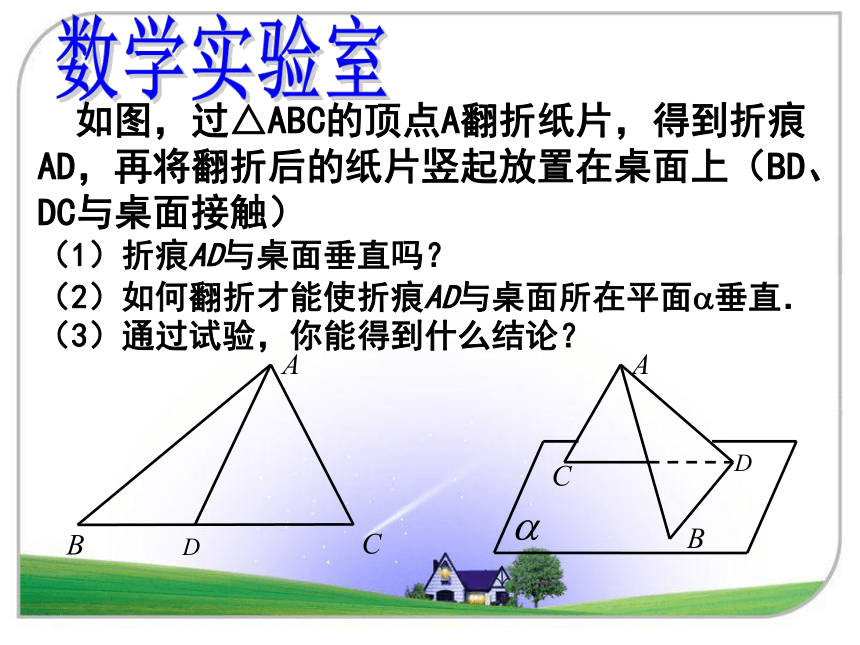
数学实验室
如图,过△ABC的顶点A翻折纸片,得到折痕AD,再将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触)
(1)折痕AD与桌面垂直吗?
(2)如何翻折才能使折痕AD与桌面所在平面?垂直.
(3)通过试验,你能得到什么结论?
数学实验报告单
1.当且仅当折痕AD 是BC 边上的高时,AD 所在直线与桌面所在平面α垂直.
2.如果一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
直线与平面垂直的判定定理
3.符号语言
一条直线与一个平面内的 都 ,则该直线与此平面垂直.
2.图形语言
两条相交直线
垂直
4.用途
1.文字语言:
慧眼辨是非
判断下列说法是否正确?
1.如果一条直线垂直于一个平面内的三角形,则该直线与平面垂直.
2.如果一条直线垂直于一个平面内的梯形,则该直线与平面垂直.
3.如果一条直线垂直于一个平面内圆的两条直径,则该直线与平面垂直.
4.如果一条直线垂直于一个平面内正六边形的两边,则该直线与平面垂直.
√
√
×
×
开动脑筋-我能行!
n
m
例1 如图所示,已知a∥b,a⊥α,求证:b⊥α.
0
a
b
α
如果两条平行线中的一条直线与一个平面垂直,那么另外一条直线也与此平面垂直.
自我测评——我更自信!
变式训练:已知四棱锥P-ABCD的底面是菱形, 且PA=PC, PB=PD.若O是AC与BD的交点,
求证: PO⊥平面ABCD.
挑战题
硕果累累
一路下来,我们结识了很多新知识,也有了很多的新想法。你能谈谈自己的收获吗?说一说,让大家一起来分享。
?我最大的收获是……??
我从同学身上学到了……
想对老师说的话……
知心话:
圆规之所以能画圆是因为它有一颗不变的心.其实,学习需要一颗不变的心,学习数学更需要一颗不变的心!
谢谢大家
必做题:课本第62页第1题
选做题:如图SA⊥平面ABC,AB⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F.求证:AF⊥SC.
探究题:课本66页的探究题.
S
B
A
C
F
E
自我测评——我更自信!
知识纵横
试试你的反应
例2 正方体ABCD-A'B'C'D',求证:AC⊥BD'
A
B
D
C
A′
B′
C
D
′
′
O
˙
知识纵横
试试你的反应
例2 已知:正方体中,AC是面对角线,BD'是与AC 异面的体对角线.求证:AC⊥BD'
A
B
D
C
A′
B′
C
D
′
′
O
知识纵横
试试你的反应
例2 已知:正方体中,AC是面对角线,BD'是与AC 异面的体对角线.求证:AC⊥BD'
A
B
D
C
A′
B′
C
D
′
′
O
因为难,所以我挑战!
例3 已知PA⊥⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过A点作AE⊥PC于点E,求证:AE⊥平面PBC.
P
A
B
C
O
E
空间直线与平面有哪几种位置关系?
直线与平面平行
直线与平面相交
直线在平面内
2.3.1直线与平面垂直的判定
自 学 提 示
自学课本第64页的内容,请思考下列问题:
1、直线与平面垂直的定义是什么?
2、怎样画直线与平面垂直?
3、用符号语言怎样表示?
限时:
3
分钟
自学——我理解了
1、定义:如果一条直线和一个平面内的 任意 一条直线都垂直,则称这条直线和这个平面垂直.
2、画法
3、符号语言
大判官
判断下列说法是否正确?
1.如果一条直线垂直于平面内的每一条直线,那么这条直线和这个平面垂直.
2.如果一条直线垂直于平面内的所有直线,那么这条直线和这个平面垂直.
3.如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直.
4.如果直线l⊥平面α,直线m?α,则l⊥m.
判断下列说法是否正确?
1.如果一条直线垂直于平面内的每一条直线,那么这条直线和这个平面垂直.
2.如果一条直线垂直于平面内的所有直线,那么这条直线和这个平面垂直.
3.如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直.
4.如果直线l⊥平面α,直线m?α,则l⊥m.
√
大判官
判断下列说法是否正确?
1.如果一条直线垂直于平面内的每一条直线,那么这条直线和这个平面垂直.
2.如果一条直线垂直于平面内的所有直线,那么这条直线和这个平面垂直.
3.如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直.
4.如果直线l⊥平面α,直线m?α,则l⊥m.
√
√
大判官
判断下列说法是否正确?
1.如果一条直线垂直于平面内的每一条直线,那么这条直线和这个平面垂直.
2.如果一条直线垂直于平面内的所有直线,那么这条直线和这个平面垂直.
3.如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直.
4.如果直线l⊥平面α,直线m?α,则l⊥m.
√
√
×
√
大判官
数学实验室
如图,过△ABC的顶点A翻折纸片,得到折痕AD,再将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触)
(1)折痕AD与桌面垂直吗?
(2)如何翻折才能使折痕AD与桌面所在平面?垂直.
(3)通过试验,你能得到什么结论?
数学实验报告单
1.当且仅当折痕AD 是BC 边上的高时,AD 所在直线与桌面所在平面α垂直.
2.如果一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
直线与平面垂直的判定定理
3.符号语言
一条直线与一个平面内的 都 ,则该直线与此平面垂直.
2.图形语言
两条相交直线
垂直
4.用途
1.文字语言:
慧眼辨是非
判断下列说法是否正确?
1.如果一条直线垂直于一个平面内的三角形,则该直线与平面垂直.
2.如果一条直线垂直于一个平面内的梯形,则该直线与平面垂直.
3.如果一条直线垂直于一个平面内圆的两条直径,则该直线与平面垂直.
4.如果一条直线垂直于一个平面内正六边形的两边,则该直线与平面垂直.
√
√
×
×
开动脑筋-我能行!
n
m
例1 如图所示,已知a∥b,a⊥α,求证:b⊥α.
0
a
b
α
如果两条平行线中的一条直线与一个平面垂直,那么另外一条直线也与此平面垂直.
自我测评——我更自信!
变式训练:已知四棱锥P-ABCD的底面是菱形, 且PA=PC, PB=PD.若O是AC与BD的交点,
求证: PO⊥平面ABCD.
挑战题
硕果累累
一路下来,我们结识了很多新知识,也有了很多的新想法。你能谈谈自己的收获吗?说一说,让大家一起来分享。
?我最大的收获是……??
我从同学身上学到了……
想对老师说的话……
知心话:
圆规之所以能画圆是因为它有一颗不变的心.其实,学习需要一颗不变的心,学习数学更需要一颗不变的心!
谢谢大家
必做题:课本第62页第1题
选做题:如图SA⊥平面ABC,AB⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F.求证:AF⊥SC.
探究题:课本66页的探究题.
S
B
A
C
F
E
自我测评——我更自信!
知识纵横
试试你的反应
例2 正方体ABCD-A'B'C'D',求证:AC⊥BD'
A
B
D
C
A′
B′
C
D
′
′
O
˙
知识纵横
试试你的反应
例2 已知:正方体中,AC是面对角线,BD'是与AC 异面的体对角线.求证:AC⊥BD'
A
B
D
C
A′
B′
C
D
′
′
O
知识纵横
试试你的反应
例2 已知:正方体中,AC是面对角线,BD'是与AC 异面的体对角线.求证:AC⊥BD'
A
B
D
C
A′
B′
C
D
′
′
O
因为难,所以我挑战!
例3 已知PA⊥⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过A点作AE⊥PC于点E,求证:AE⊥平面PBC.
P
A
B
C
O
E
