高中数学人教A版必修2第一章1.2.1 中心投影与平行投影&1.2.2 空间几何体的三视图课件(40张PPT)
文档属性
| 名称 | 高中数学人教A版必修2第一章1.2.1 中心投影与平行投影&1.2.2 空间几何体的三视图课件(40张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 20:53:01 | ||
图片预览





文档简介
1.2 空间几何体的投影和三视图
铜梁中学数学组 张洋
1.新课引入:
前面我们认识了柱体、锥体、台体、球体以及简单组合体的结构特征。为了将这些空间几何体画在纸上,用平面图形表示出来,使我们能够根据平面图形想象空间几何体的形状和结构,这就需要学习视图有关知识。
2.课堂探究:
我们知道,光是直线传播的。由于光的照射,在不透明物体的后面的屏幕上可以留下这个物体的影子,这种现象叫做投影。其中,我们把光线叫做投影线,把留下物体影子的屏幕叫做投影面。
2.1.中心投影
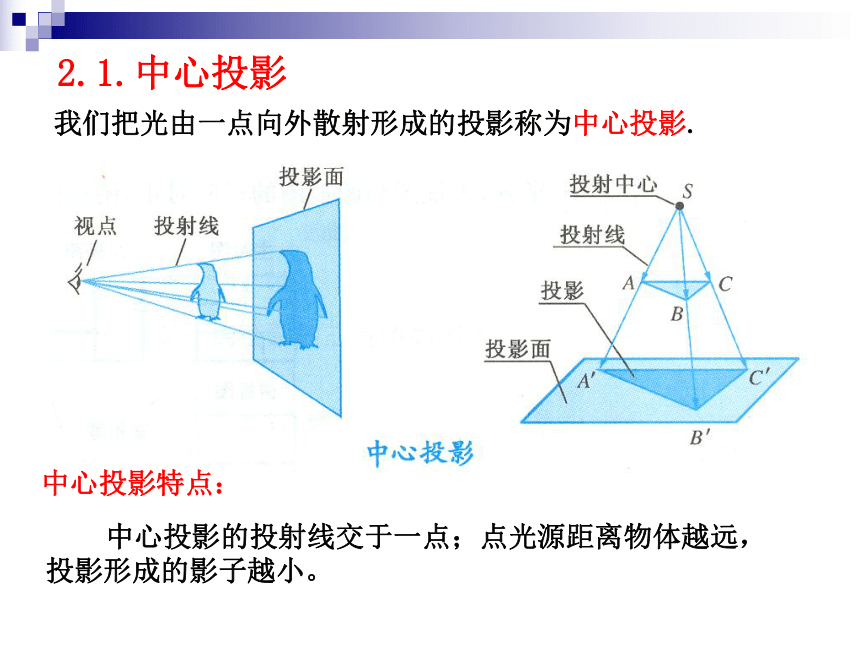
我们把光由一点向外散射形成的投影称为中心投影.
中心投影特点:
中心投影的投射线交于一点;点光源距离物体越远,投影形成的影子越小。
中心投影后的图形与原图形相比,虽然改变很多,但直观性强,看起来与人的视觉效果一致,最像原来的物体.所以在绘画时,经常使用这种方法,但在立体几何中很少用中心投影原理来画图.
2.1.中心投影
我们把光由一点向外散射形成的投影称为中心投影.
中心投影特点:
中心投影的投射线交于一点;点光源距离物体越远,投影形成的影子越小。
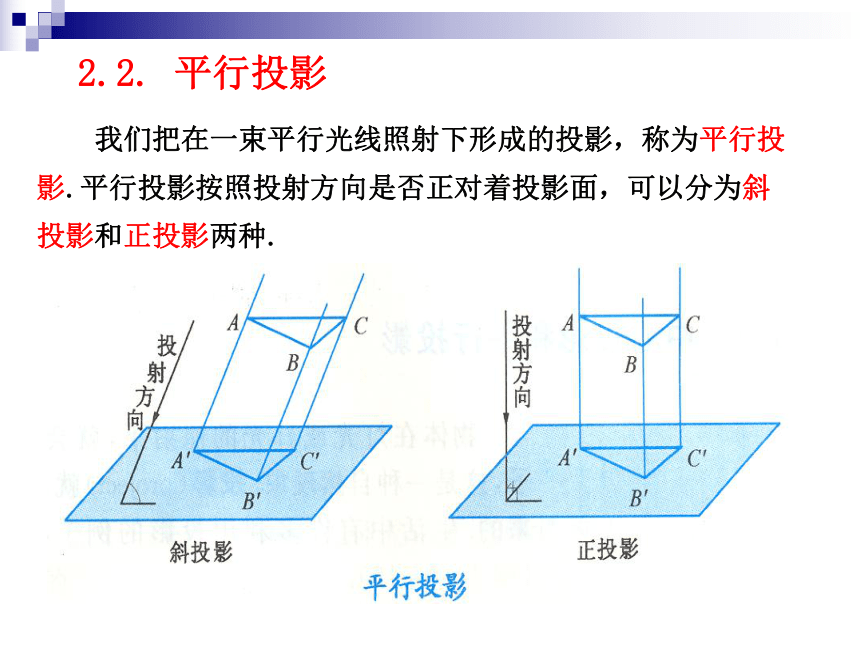
我们把在一束平行光线照射下形成的投影,称为平行投影.平行投影按照投射方向是否正对着投影面,可以分为斜投影和正投影两种.
2.2. 平行投影
斜投影:投射线不正对着投影面
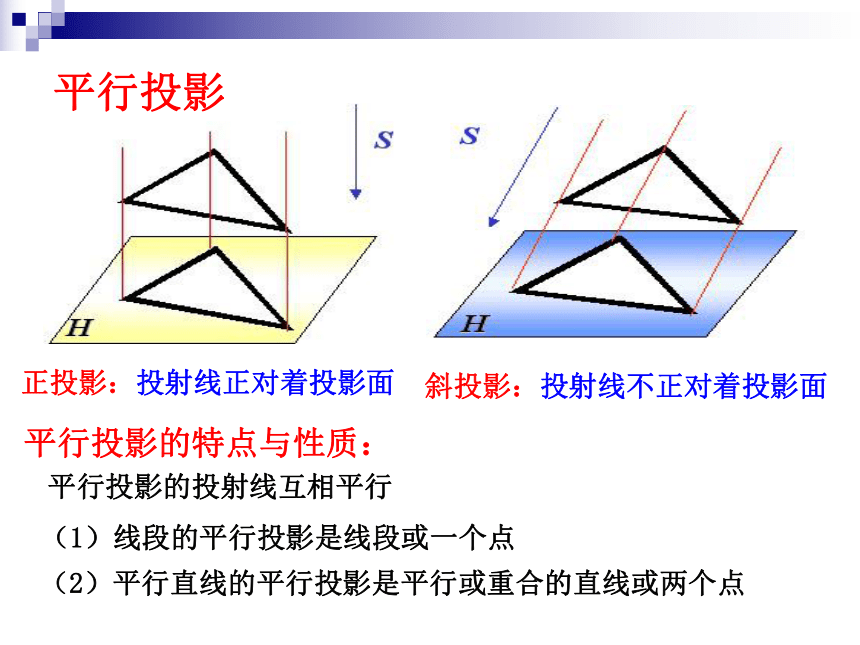
平行投影
正投影:投射线正对着投影面
平行投影的特点与性质:
平行投影的投射线互相平行
(1)线段的平行投影是线段或一个点
(2)平行直线的平行投影是平行或重合的直线或两个点
斜投影:投射线不正对着投影面
平行投影
正投影:投射线正对着投影面
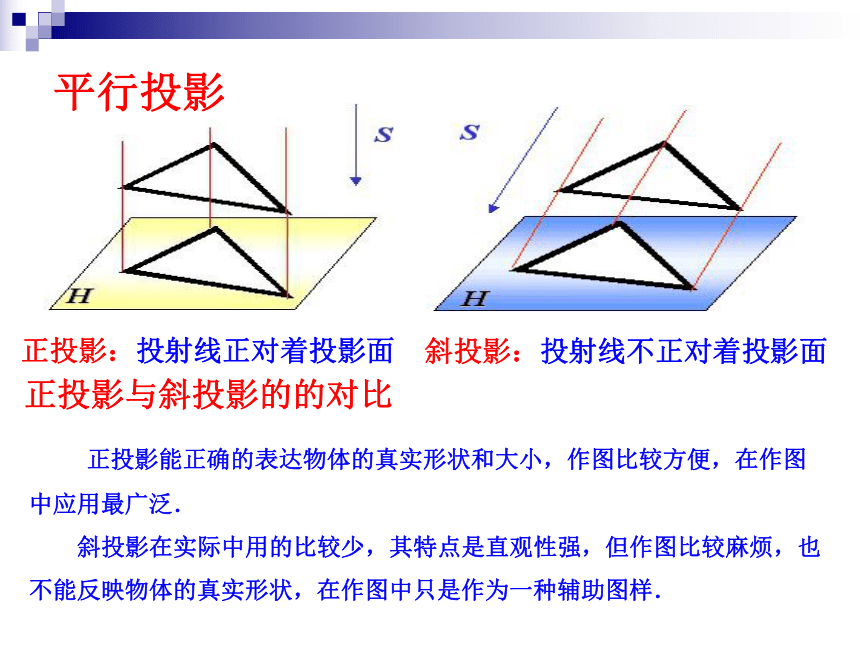
正投影与斜投影的的对比
正投影能正确的表达物体的真实形状和大小,作图比较方便,在作图中应用最广泛.
斜投影在实际中用的比较少,其特点是直观性强,但作图比较麻烦,也不能反映物体的真实形状,在作图中只是作为一种辅助图样.
S
投射方向
投射方向
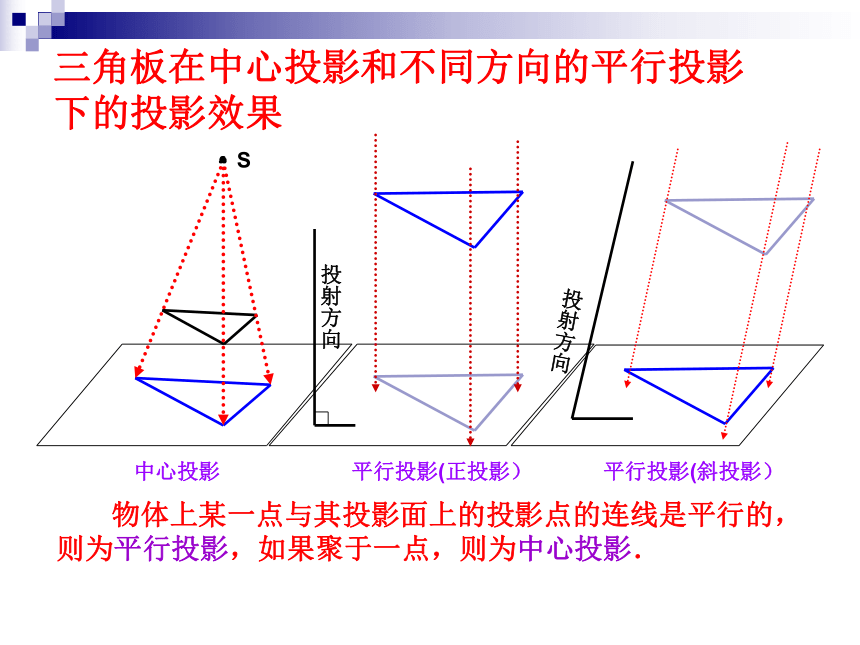
三角板在中心投影和不同方向的平行投影下的投影效果
物体上某一点与其投影面上的投影点的连线是平行的,则为平行投影,如果聚于一点,则为中心投影.
中心投影 平行投影(正投影) 平行投影(斜投影)
3.空间几何体的三视图
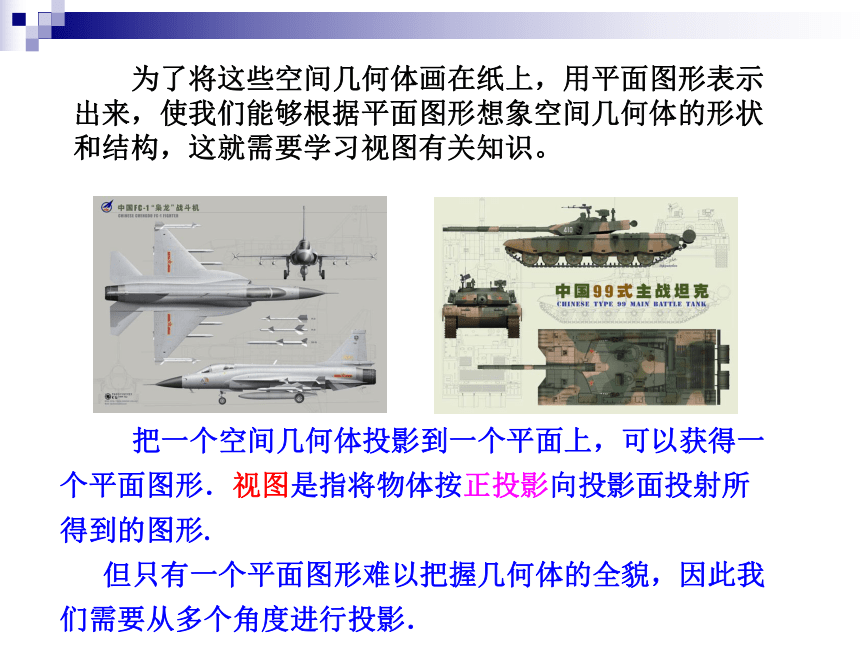
为了将这些空间几何体画在纸上,用平面图形表示出来,使我们能够根据平面图形想象空间几何体的形状和结构,这就需要学习视图有关知识。
把一个空间几何体投影到一个平面上,可以获得一个平面图形.视图是指将物体按正投影向投影面投射所得到的图形.
但只有一个平面图形难以把握几何体的全貌,因此我们需要从多个角度进行投影.
把一个空间几何体投影到一个平面上,可以获得一个平面图形.视图是指将物体按正投影向投影面投射所得到的图形.
但只有一个平面图形难以把握几何体的全貌,因此我们需要从多个角度进行投影.
三 视 图
1.光线从几何体的前面向后面正投影所得到的投影图
叫做几何体的正视图.
2.光线从几何体的左面向右面正投影所得到的投影图
叫做几何体的侧视图.
3.光线从几何体的上面向下面正投影所得到的投影图
叫做几何体的俯视图.
三视图
几何体的正视图、侧视图和俯视图统称为几何体的三视图.
俯视图
正视图
俯视图
正视图
侧视图
侧视图
根据长方体的模型,请您画出它 们的三视图,并观察三种图形之间有什么关系?
长度
高度
宽度
高平齐
宽相等
空间几何体的三视图
如何将三个视图画到平面上?
长对正
高平齐
宽相等
三视图的特点
一般地,侧视图在正视图的右边,俯视图在正视图的下边
4.基本几何体三视图
上一节学习的棱柱、棱锥、棱台以及圆台的三视图是怎样的?
六棱柱
正
侧
俯
棱柱的三视图
正三棱锥
正
侧
俯
棱锥的三视图
棱锥的三视图
正四棱锥
正
侧
俯
棱台的三视图
正四棱台
侧
俯
正
圆台
侧
俯
圆台的三视图
正
遮挡住看不见的线用虚线表示
简单组合体的三视图
画出右图所示物体的俯视图.
该物体可以看作是由两个圆台组合而成的,俯视有不可见边界轮廓线(用虚线表示).
侧视
练习:改一改:某同学画的下图物体的三视图,对吗?若有错,请指出并改正.
正视图
侧视图
俯视图
对
错
错
俯视
正视
从前面正对着物体观察,画出正视图,正视图反映了物体的长和高及前后两个面的实形.
从上向下正对着物体观察,画出俯视图,布置在正视图的正下方,俯视图反映了物体的长和宽及上下两个面的实形.
三视图表达的意义
从左向右正对着物体观察,画出侧视图,布置在正视图的正右方,侧视图反映了物体的宽和高及左右两个面的实形.
三视图能反映物体真实的形状和长、宽、高.
1.投影的分类
中心投影:投射线交于一点
平行投影
斜投影
正投影(本节主要学习利用正投影绘制空间图形的三视图,并能根据所给的三视图了解该空间图形的基本特征)
投射线平行
2.几何体的三视图:正视图,侧视图,俯视图
三视图的作图步骤
正视图方向
侧视图方向
俯视图方向
2.运用长对正、高平齐、宽相等的原则画出其它视图
1. 位置
正视图 侧视图 俯视图
例1、画下列几何体的三视图
练习2:画出下面正三棱锥的三视图.
正三棱锥
侧
俯
正
例2、画下列几何体的三视图
例3、画下列几何体的三视图
如果要做一个水管的三叉接头,工人事先看到的不是图1,而是图2,然后根据这三个图形制造出水管接头.
图1
三通水管
图2
练习3:画出下面组合体的的三视图。
圆柱
侧
俯
1.请您画出下列几何体的三视图
(1) 圆柱的三视图
正
侧
俯
(2) 圆锥的三视图
正
侧
俯
(3)圆台的三视图
正
侧
俯
(4)六棱柱的三视图
正
(5) 六棱锥的三视图
侧
俯
正
正
侧
俯
(6) 四棱台的三视图
侧
俯
(7) 球的三视图
正
(1) 四棱柱
(2) 圆锥与半球组成的简单组合体
(3) 四棱柱与球组成的简单组合体
(4) 两个圆台组成的简单组合体
遮挡住看不见的线用虚线
3.画出下面这个组合图形的三视图.
铜梁中学数学组 张洋
1.新课引入:
前面我们认识了柱体、锥体、台体、球体以及简单组合体的结构特征。为了将这些空间几何体画在纸上,用平面图形表示出来,使我们能够根据平面图形想象空间几何体的形状和结构,这就需要学习视图有关知识。
2.课堂探究:
我们知道,光是直线传播的。由于光的照射,在不透明物体的后面的屏幕上可以留下这个物体的影子,这种现象叫做投影。其中,我们把光线叫做投影线,把留下物体影子的屏幕叫做投影面。
2.1.中心投影
我们把光由一点向外散射形成的投影称为中心投影.
中心投影特点:
中心投影的投射线交于一点;点光源距离物体越远,投影形成的影子越小。
中心投影后的图形与原图形相比,虽然改变很多,但直观性强,看起来与人的视觉效果一致,最像原来的物体.所以在绘画时,经常使用这种方法,但在立体几何中很少用中心投影原理来画图.
2.1.中心投影
我们把光由一点向外散射形成的投影称为中心投影.
中心投影特点:
中心投影的投射线交于一点;点光源距离物体越远,投影形成的影子越小。
我们把在一束平行光线照射下形成的投影,称为平行投影.平行投影按照投射方向是否正对着投影面,可以分为斜投影和正投影两种.
2.2. 平行投影
斜投影:投射线不正对着投影面
平行投影
正投影:投射线正对着投影面
平行投影的特点与性质:
平行投影的投射线互相平行
(1)线段的平行投影是线段或一个点
(2)平行直线的平行投影是平行或重合的直线或两个点
斜投影:投射线不正对着投影面
平行投影
正投影:投射线正对着投影面
正投影与斜投影的的对比
正投影能正确的表达物体的真实形状和大小,作图比较方便,在作图中应用最广泛.
斜投影在实际中用的比较少,其特点是直观性强,但作图比较麻烦,也不能反映物体的真实形状,在作图中只是作为一种辅助图样.
S
投射方向
投射方向
三角板在中心投影和不同方向的平行投影下的投影效果
物体上某一点与其投影面上的投影点的连线是平行的,则为平行投影,如果聚于一点,则为中心投影.
中心投影 平行投影(正投影) 平行投影(斜投影)
3.空间几何体的三视图
为了将这些空间几何体画在纸上,用平面图形表示出来,使我们能够根据平面图形想象空间几何体的形状和结构,这就需要学习视图有关知识。
把一个空间几何体投影到一个平面上,可以获得一个平面图形.视图是指将物体按正投影向投影面投射所得到的图形.
但只有一个平面图形难以把握几何体的全貌,因此我们需要从多个角度进行投影.
把一个空间几何体投影到一个平面上,可以获得一个平面图形.视图是指将物体按正投影向投影面投射所得到的图形.
但只有一个平面图形难以把握几何体的全貌,因此我们需要从多个角度进行投影.
三 视 图
1.光线从几何体的前面向后面正投影所得到的投影图
叫做几何体的正视图.
2.光线从几何体的左面向右面正投影所得到的投影图
叫做几何体的侧视图.
3.光线从几何体的上面向下面正投影所得到的投影图
叫做几何体的俯视图.
三视图
几何体的正视图、侧视图和俯视图统称为几何体的三视图.
俯视图
正视图
俯视图
正视图
侧视图
侧视图
根据长方体的模型,请您画出它 们的三视图,并观察三种图形之间有什么关系?
长度
高度
宽度
高平齐
宽相等
空间几何体的三视图
如何将三个视图画到平面上?
长对正
高平齐
宽相等
三视图的特点
一般地,侧视图在正视图的右边,俯视图在正视图的下边
4.基本几何体三视图
上一节学习的棱柱、棱锥、棱台以及圆台的三视图是怎样的?
六棱柱
正
侧
俯
棱柱的三视图
正三棱锥
正
侧
俯
棱锥的三视图
棱锥的三视图
正四棱锥
正
侧
俯
棱台的三视图
正四棱台
侧
俯
正
圆台
侧
俯
圆台的三视图
正
遮挡住看不见的线用虚线表示
简单组合体的三视图
画出右图所示物体的俯视图.
该物体可以看作是由两个圆台组合而成的,俯视有不可见边界轮廓线(用虚线表示).
侧视
练习:改一改:某同学画的下图物体的三视图,对吗?若有错,请指出并改正.
正视图
侧视图
俯视图
对
错
错
俯视
正视
从前面正对着物体观察,画出正视图,正视图反映了物体的长和高及前后两个面的实形.
从上向下正对着物体观察,画出俯视图,布置在正视图的正下方,俯视图反映了物体的长和宽及上下两个面的实形.
三视图表达的意义
从左向右正对着物体观察,画出侧视图,布置在正视图的正右方,侧视图反映了物体的宽和高及左右两个面的实形.
三视图能反映物体真实的形状和长、宽、高.
1.投影的分类
中心投影:投射线交于一点
平行投影
斜投影
正投影(本节主要学习利用正投影绘制空间图形的三视图,并能根据所给的三视图了解该空间图形的基本特征)
投射线平行
2.几何体的三视图:正视图,侧视图,俯视图
三视图的作图步骤
正视图方向
侧视图方向
俯视图方向
2.运用长对正、高平齐、宽相等的原则画出其它视图
1. 位置
正视图 侧视图 俯视图
例1、画下列几何体的三视图
练习2:画出下面正三棱锥的三视图.
正三棱锥
侧
俯
正
例2、画下列几何体的三视图
例3、画下列几何体的三视图
如果要做一个水管的三叉接头,工人事先看到的不是图1,而是图2,然后根据这三个图形制造出水管接头.
图1
三通水管
图2
练习3:画出下面组合体的的三视图。
圆柱
侧
俯
1.请您画出下列几何体的三视图
(1) 圆柱的三视图
正
侧
俯
(2) 圆锥的三视图
正
侧
俯
(3)圆台的三视图
正
侧
俯
(4)六棱柱的三视图
正
(5) 六棱锥的三视图
侧
俯
正
正
侧
俯
(6) 四棱台的三视图
侧
俯
(7) 球的三视图
正
(1) 四棱柱
(2) 圆锥与半球组成的简单组合体
(3) 四棱柱与球组成的简单组合体
(4) 两个圆台组成的简单组合体
遮挡住看不见的线用虚线
3.画出下面这个组合图形的三视图.
