高中数学人教A版必修二 4.1.1 圆的标准方程 课件(17张PPT)
文档属性
| 名称 | 高中数学人教A版必修二 4.1.1 圆的标准方程 课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 747.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 21:22:56 | ||
图片预览


文档简介
第四章 第一节 第一课时
厚德
自强
博学
创新
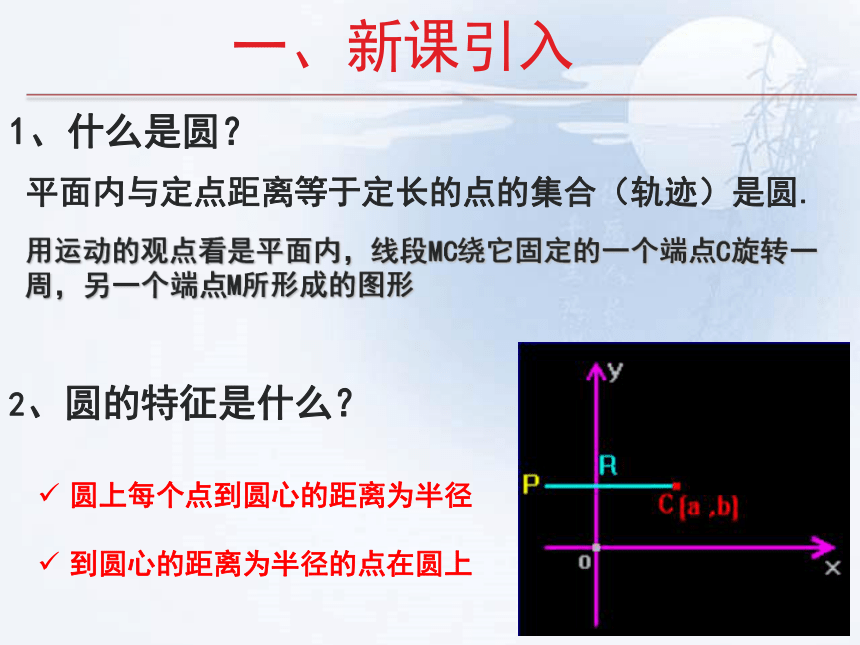
2、圆的特征是什么?
圆上每个点到圆心的距离为半径
到圆心的距离为半径的点在圆上
平面内与定点距离等于定长的点的集合(轨迹)是圆.
1、什么是圆?
一、新课引入
用运动的观点看是平面内,线段MC绕它固定的一个端点C旋转一周,另一个端点M所形成的图形
O
y
x
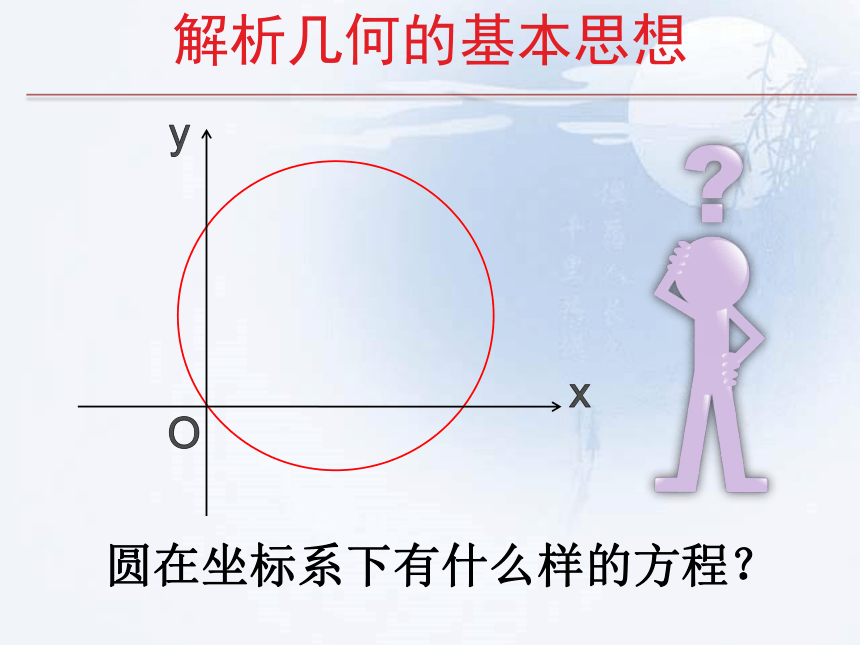
圆在坐标系下有什么样的方程?
解析几何的基本思想
O
x
y
C(a,b)
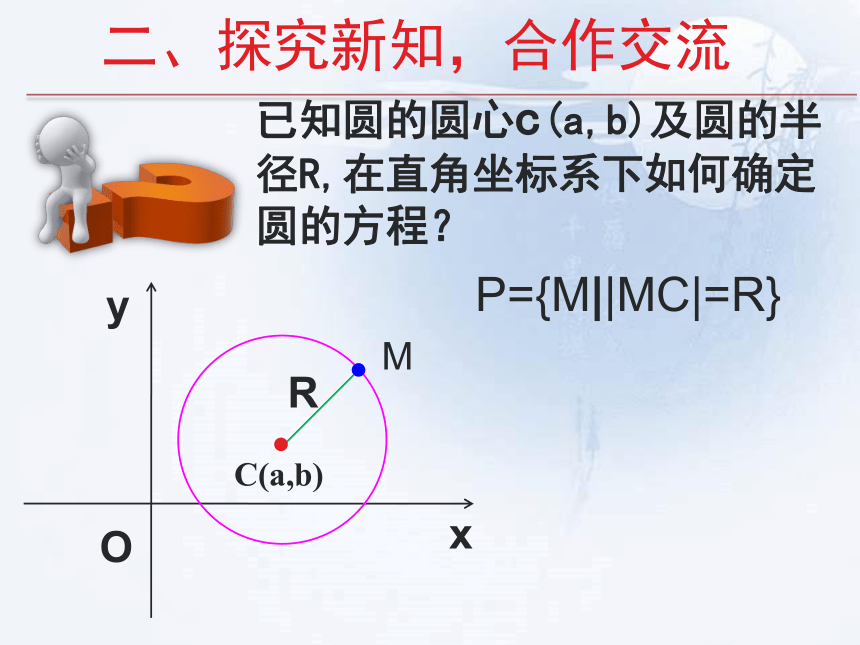
二、探究新知,合作交流
已知圆的圆心c(a,b)及圆的半径R,在直角坐标系下如何确定圆的方程?
M
R
P={M||MC|=R}
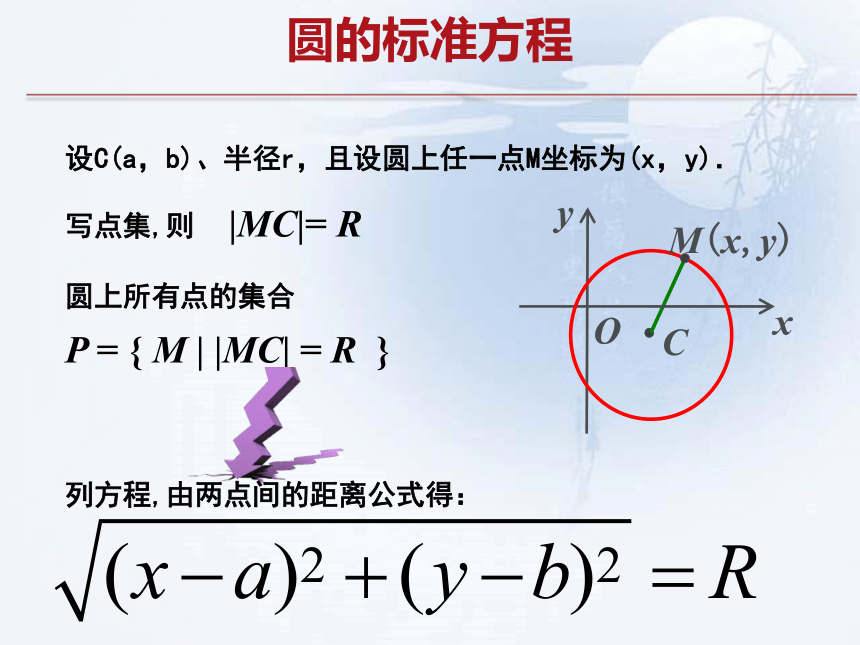
圆的标准方程
|MC|= R
写点集,则
P = { M | |MC| = R }
圆上所有点的集合
y
x
O
C
M(x,y)
设C(a,b)、半径r,且设圆上任一点M坐标为(x,y).
列方程,由两点间的距离公式得:
x
y
O
C
M(x,y)
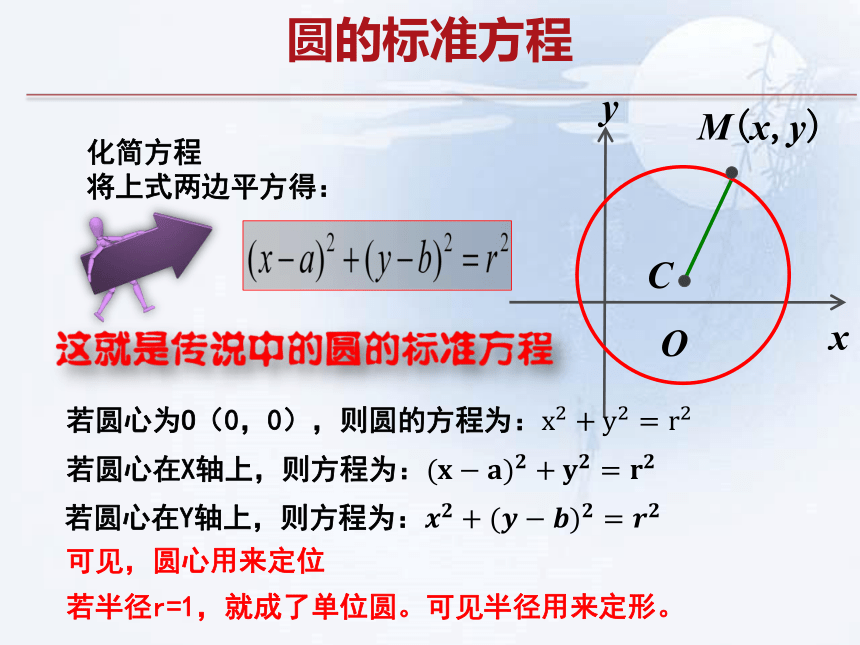
若圆心为O(0,0),则圆的方程为:x2+y2=r2
?
化简方程
将上式两边平方得:
若圆心在Y轴上,则方程为:????????+(?????????)????=????????
?
若圆心在X轴上,则方程为:(?????????)????+????????=????????
?
圆的标准方程
若半径r=1,就成了单位圆。可见半径用来定形。
可见,圆心用来定位
圆的方程形式有什么特点?
圆心和半径分别确定了圆的位置和大小,从而确定了圆,所以,只要a,b,r三个量确定了且r>0,圆的方程就给定了.这就是说要确定圆的方程,必须具备三个独立的条件
这是二元二次方程,括号内变数x,y的系数都是1.点(a,b)、r分别表示圆心的坐标和圆的半径.
特点:
结论:
基础演练
(m≠0)
(1)说出下列圆的圆心和半径:
(2)圆心是(3,-3),半径是2的圆是______________________________.
(3)以(3,4)为圆心,且过点(0,0)的圆的方程为__________________________________.
(?????????)????+(????+????)????=????
?
(?????????)????+(?????????)????=????????
?
(-2,0) |m|
(3,2) ????
?
△ABC的三个顶点的坐标分别是A(5,1),B(7,-3),
C(2,-8),求它的外接圆的标准方程.
解:设所求圆的方程是(?????????)????+(?????????)????=????????
因为A(5,1),B(7,-3),C(2,-8)都在圆上,
所以它们的坐标都满足方程(1),
于是(?????????)????+(?????????)????=????????(?????????)????+(??????????)????=????????(?????????)????+(??????????)????=???????? ???????????=????????=?????????=????
所求圆的方程为:(?????????)????+(????+????)????=????????
?
待定系数法
x
y
o
A
B
C
m
n
D
r
△ABC的三个顶点的坐标分别是A(5,1),
B(7,-3),C(2,-8),求它的外接圆的标准方程.
已知圆心为C的圆经过A(1,1)和B(2,-2),且圆心在直线 l :x-y+1=0上,求圆心为C的圆的标准方程。
A
B
l :x-y+1=0
C
知识探究:点与圆的位置关系 有几种?
三种:点在圆内、在圆上、在圆外
知识点:
四、点与圆的位置关系
点在圆内、在圆上、在圆外
M
O
|OM||OM|=r
O
M
O
M
|OM|>r
点在圆内
点在圆上
点在圆外
在平面几何中,如何确定点与圆的位置关系呢?
若(x0-a)2+(y0-b)2>r2时, 点M在圆C外;
若(x0-a)2+(y0-b)2=r2时,点M在圆C上;
若(x0-a)2+(y0-b)2设点M ,圆 :
知识点五:判断点与圆的位置关系的方法:
把点M 的坐标代入圆的方程
例:写出圆心为 ,半径长等于5的圆的方程,并判断点 ,
是否在这个圆上。
解:圆心是 ,半径长等于5的圆的标准方程 是:
把 的坐标代入圆的方
程 ,可知:
典型例题
点N在圆上,点M在圆外,点A在圆内
特殊位置的圆的方程:
圆心在原点:
x2 + y2 = r2 (r≠0)
圆心在x轴上:
(x ? a)2 + y2 = r2 (r≠0)
圆心在y轴上:
x2+ (y ? b)2 = r2 (r≠0)
圆过原点:
(x ? a)2 + (y-b)2 = b2 (b≠0)
圆心在x轴上且过原点:
(x ? a)2 + y2 = a2 (a≠0)
圆心在y轴上且过原点:
x 2 + (y-b)2 = b2 (b≠0)
圆与x轴相切:
(x ? a)2 + (y-b)2 = a2+b2 (a2+b2≠0)
圆与y轴相切:
(x ? a)2 + (y-b)2 = a2 (a≠0)
圆与x,y轴都相切:
(x ? a)2 + (y±a)2 = a2 (a≠0)
圆心C(a,b),半径r
特别提示:若圆心为O(0,0),则圆的标准方程为:
3、求圆的标准方程的方法:
几何方法:数形结合
代数方法:待定系数法求
1、圆的标准方程
2. 数型结合的数学思想
四、小结
厚德
自强
博学
创新
2、圆的特征是什么?
圆上每个点到圆心的距离为半径
到圆心的距离为半径的点在圆上
平面内与定点距离等于定长的点的集合(轨迹)是圆.
1、什么是圆?
一、新课引入
用运动的观点看是平面内,线段MC绕它固定的一个端点C旋转一周,另一个端点M所形成的图形
O
y
x
圆在坐标系下有什么样的方程?
解析几何的基本思想
O
x
y
C(a,b)
二、探究新知,合作交流
已知圆的圆心c(a,b)及圆的半径R,在直角坐标系下如何确定圆的方程?
M
R
P={M||MC|=R}
圆的标准方程
|MC|= R
写点集,则
P = { M | |MC| = R }
圆上所有点的集合
y
x
O
C
M(x,y)
设C(a,b)、半径r,且设圆上任一点M坐标为(x,y).
列方程,由两点间的距离公式得:
x
y
O
C
M(x,y)
若圆心为O(0,0),则圆的方程为:x2+y2=r2
?
化简方程
将上式两边平方得:
若圆心在Y轴上,则方程为:????????+(?????????)????=????????
?
若圆心在X轴上,则方程为:(?????????)????+????????=????????
?
圆的标准方程
若半径r=1,就成了单位圆。可见半径用来定形。
可见,圆心用来定位
圆的方程形式有什么特点?
圆心和半径分别确定了圆的位置和大小,从而确定了圆,所以,只要a,b,r三个量确定了且r>0,圆的方程就给定了.这就是说要确定圆的方程,必须具备三个独立的条件
这是二元二次方程,括号内变数x,y的系数都是1.点(a,b)、r分别表示圆心的坐标和圆的半径.
特点:
结论:
基础演练
(m≠0)
(1)说出下列圆的圆心和半径:
(2)圆心是(3,-3),半径是2的圆是______________________________.
(3)以(3,4)为圆心,且过点(0,0)的圆的方程为__________________________________.
(?????????)????+(????+????)????=????
?
(?????????)????+(?????????)????=????????
?
(-2,0) |m|
(3,2) ????
?
△ABC的三个顶点的坐标分别是A(5,1),B(7,-3),
C(2,-8),求它的外接圆的标准方程.
解:设所求圆的方程是(?????????)????+(?????????)????=????????
因为A(5,1),B(7,-3),C(2,-8)都在圆上,
所以它们的坐标都满足方程(1),
于是(?????????)????+(?????????)????=????????(?????????)????+(??????????)????=????????(?????????)????+(??????????)????=???????? ???????????=????????=?????????=????
所求圆的方程为:(?????????)????+(????+????)????=????????
?
待定系数法
x
y
o
A
B
C
m
n
D
r
△ABC的三个顶点的坐标分别是A(5,1),
B(7,-3),C(2,-8),求它的外接圆的标准方程.
已知圆心为C的圆经过A(1,1)和B(2,-2),且圆心在直线 l :x-y+1=0上,求圆心为C的圆的标准方程。
A
B
l :x-y+1=0
C
知识探究:点与圆的位置关系 有几种?
三种:点在圆内、在圆上、在圆外
知识点:
四、点与圆的位置关系
点在圆内、在圆上、在圆外
M
O
|OM|
O
M
O
M
|OM|>r
点在圆内
点在圆上
点在圆外
在平面几何中,如何确定点与圆的位置关系呢?
若(x0-a)2+(y0-b)2>r2时, 点M在圆C外;
若(x0-a)2+(y0-b)2=r2时,点M在圆C上;
若(x0-a)2+(y0-b)2
知识点五:判断点与圆的位置关系的方法:
把点M 的坐标代入圆的方程
例:写出圆心为 ,半径长等于5的圆的方程,并判断点 ,
是否在这个圆上。
解:圆心是 ,半径长等于5的圆的标准方程 是:
把 的坐标代入圆的方
程 ,可知:
典型例题
点N在圆上,点M在圆外,点A在圆内
特殊位置的圆的方程:
圆心在原点:
x2 + y2 = r2 (r≠0)
圆心在x轴上:
(x ? a)2 + y2 = r2 (r≠0)
圆心在y轴上:
x2+ (y ? b)2 = r2 (r≠0)
圆过原点:
(x ? a)2 + (y-b)2 = b2 (b≠0)
圆心在x轴上且过原点:
(x ? a)2 + y2 = a2 (a≠0)
圆心在y轴上且过原点:
x 2 + (y-b)2 = b2 (b≠0)
圆与x轴相切:
(x ? a)2 + (y-b)2 = a2+b2 (a2+b2≠0)
圆与y轴相切:
(x ? a)2 + (y-b)2 = a2 (a≠0)
圆与x,y轴都相切:
(x ? a)2 + (y±a)2 = a2 (a≠0)
圆心C(a,b),半径r
特别提示:若圆心为O(0,0),则圆的标准方程为:
3、求圆的标准方程的方法:
几何方法:数形结合
代数方法:待定系数法求
1、圆的标准方程
2. 数型结合的数学思想
四、小结
