高中数学人教A版必修二:4.2.2 圆与圆的位置关系 课件(16张PPT)
文档属性
| 名称 | 高中数学人教A版必修二:4.2.2 圆与圆的位置关系 课件(16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 623.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 21:03:41 | ||
图片预览





文档简介
在现实生活中,我们总能见到一些现象,从这些想象中,不知道同学们作何感想?它们告诉了你们什么信息?
4.2.2 圆与圆的位置关系
圆与圆有哪几种位置关系?
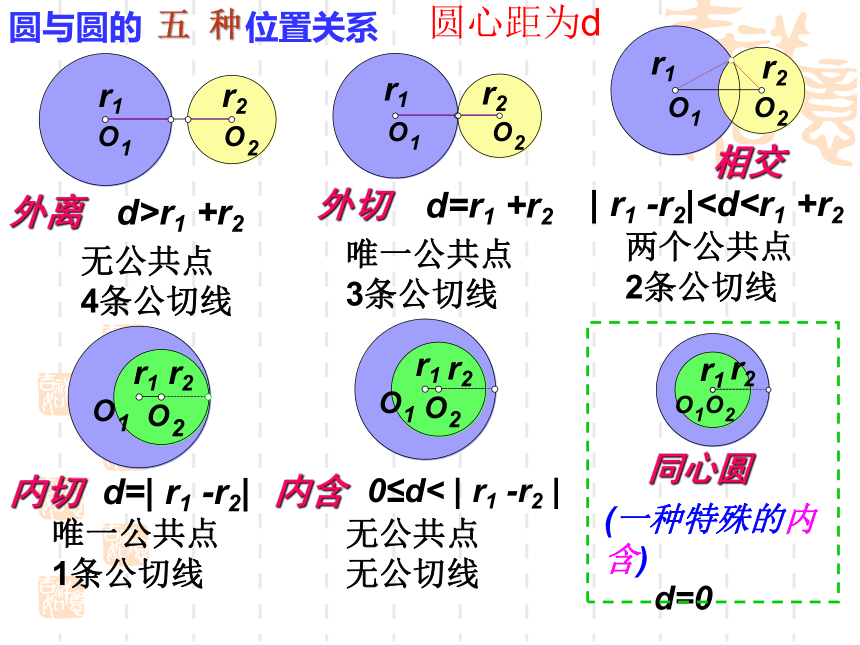
圆与圆的 位置关系
外离
d>r1 +r2
d=r1 +r2
| r1 -r2|d=| r1 -r2|
0≤d< | r1 -r2 |
外切
相交
内切
内含
五 种
d=0
同心圆
(一种特殊的内含)
无公共点 4条公切线
唯一公共点 3条公切线
两个公共点 2条公切线
唯一公共点 1条公切线
无公共点 无公切线
圆心距为d
r2
O
1
O
2
r1
O
1
O
2
r1
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r1
r2
O
1
O
2
r1
r2
O
1
O
2
r1
r2
例1 设圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-2=0,试判断圆C1与圆C2的关系.
x
y
A
B
O
C1
C2
(3,-1)
(-1,1)
.
.
(2,2)
(-1,-4)
x+2y-1=0
判断C1和C2的位置关系
解:联立两个方程组得
①-②得
把上式代入①
①
②
④
所以方程④有两个不相等的实根x1,x2
把x1,x2代入方程③得到y1,y2
③
所以圆C1与圆C2有两个不同的交点A(x1,y1),B(x2,y2)
联立方程组
消去二次项
消元得一元二次方程
用Δ判断两圆的位置关系
解法二: 把圆C1的方程化为标准方程,得
圆C1的圆心是点(-1,-4),半径长r1=5.
把圆C2的方程化为标准方程,得
圆C1的圆心是点(2,2),半径长r2= .
圆C1与圆C2的连心线长为
圆C1与圆C2的半径之和是
两半径之差是
所以圆C1与圆C2相交
求两圆心坐标及半径 (配方法)
求圆心距d
(两点间距离公式)
比较d和r1,r2的大小,下结论
反思
判断两圆位置关系
几何方法
代数方法
各有何优劣,如何选用?
(1)当Δ=0时,有一个交点,两圆位置关系如何?
内切或外切
(2)当Δ<0时,没有交点,两圆位置关系如何?
几何方法直观,但不能 求出交点;
代数方法能求出交点,但Δ=0, Δ<0时,不能判
圆的位置关系。
内含或相离
两圆相交时,相交弦所在直线方程为两圆方程相减的一次方程
教材129探究
1. 过两圆x2 + y2 + 6x –4 = 0 和 x2 + y2 + 6y –28 = 0的交点且圆心在直线x-y-4=0上的圆方程是( )
A.x2+y2-x-5y+2=0 B.x2+y2-x-5y-2=0
C.x2+y2-x+7y-32=0 D.x2+y2+x+7y+32=0
巩固练习
C
2.若圆x2 + y2 – 2x –5 = 0 和 圆x2 + y2 +2x – 4y –4 = 0的交点为A,B,则线段AB的垂直平分线的方程是( )
A. x + y – 1=0
B. 2x – y + 1=0
C. x –2 y + 1=0
D. x – y + 1=0
A
小结:判断两圆位置关系
几何方法
两圆心坐标及半径(配方法)
圆心距d
(两点间距离公式)
比较d和r1,r2的大小,下结论
代数方法
消去y(或x)
圆与圆的位置关系
|O1O2|=|R-r|
内切
r
R
O
1
O
2
外离
|O1O2|>|R+r|
r
R
O
1
O
2
0≤|O1O2|<|R-r|
内含
r
R
O
1
O
2
外切
r
R
O
1
O
2
|O1O2|=|R+r|
|R-r|<|O1O2|<|R+r|
相交
r
R
O
1
O
2
唯一公共点 1条公切线
唯一公共点 3条公切线
两个公共点 2条公切线
无公共点 4条公切线
无公共点 无公切线
4.2.2 圆与圆的位置关系
圆与圆有哪几种位置关系?
圆与圆的 位置关系
外离
d>r1 +r2
d=r1 +r2
| r1 -r2|
0≤d< | r1 -r2 |
外切
相交
内切
内含
五 种
d=0
同心圆
(一种特殊的内含)
无公共点 4条公切线
唯一公共点 3条公切线
两个公共点 2条公切线
唯一公共点 1条公切线
无公共点 无公切线
圆心距为d
r2
O
1
O
2
r1
O
1
O
2
r1
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r1
r2
O
1
O
2
r1
r2
O
1
O
2
r1
r2
例1 设圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-2=0,试判断圆C1与圆C2的关系.
x
y
A
B
O
C1
C2
(3,-1)
(-1,1)
.
.
(2,2)
(-1,-4)
x+2y-1=0
判断C1和C2的位置关系
解:联立两个方程组得
①-②得
把上式代入①
①
②
④
所以方程④有两个不相等的实根x1,x2
把x1,x2代入方程③得到y1,y2
③
所以圆C1与圆C2有两个不同的交点A(x1,y1),B(x2,y2)
联立方程组
消去二次项
消元得一元二次方程
用Δ判断两圆的位置关系
解法二: 把圆C1的方程化为标准方程,得
圆C1的圆心是点(-1,-4),半径长r1=5.
把圆C2的方程化为标准方程,得
圆C1的圆心是点(2,2),半径长r2= .
圆C1与圆C2的连心线长为
圆C1与圆C2的半径之和是
两半径之差是
所以圆C1与圆C2相交
求两圆心坐标及半径 (配方法)
求圆心距d
(两点间距离公式)
比较d和r1,r2的大小,下结论
反思
判断两圆位置关系
几何方法
代数方法
各有何优劣,如何选用?
(1)当Δ=0时,有一个交点,两圆位置关系如何?
内切或外切
(2)当Δ<0时,没有交点,两圆位置关系如何?
几何方法直观,但不能 求出交点;
代数方法能求出交点,但Δ=0, Δ<0时,不能判
圆的位置关系。
内含或相离
两圆相交时,相交弦所在直线方程为两圆方程相减的一次方程
教材129探究
1. 过两圆x2 + y2 + 6x –4 = 0 和 x2 + y2 + 6y –28 = 0的交点且圆心在直线x-y-4=0上的圆方程是( )
A.x2+y2-x-5y+2=0 B.x2+y2-x-5y-2=0
C.x2+y2-x+7y-32=0 D.x2+y2+x+7y+32=0
巩固练习
C
2.若圆x2 + y2 – 2x –5 = 0 和 圆x2 + y2 +2x – 4y –4 = 0的交点为A,B,则线段AB的垂直平分线的方程是( )
A. x + y – 1=0
B. 2x – y + 1=0
C. x –2 y + 1=0
D. x – y + 1=0
A
小结:判断两圆位置关系
几何方法
两圆心坐标及半径(配方法)
圆心距d
(两点间距离公式)
比较d和r1,r2的大小,下结论
代数方法
消去y(或x)
圆与圆的位置关系
|O1O2|=|R-r|
内切
r
R
O
1
O
2
外离
|O1O2|>|R+r|
r
R
O
1
O
2
0≤|O1O2|<|R-r|
内含
r
R
O
1
O
2
外切
r
R
O
1
O
2
|O1O2|=|R+r|
|R-r|<|O1O2|<|R+r|
相交
r
R
O
1
O
2
唯一公共点 1条公切线
唯一公共点 3条公切线
两个公共点 2条公切线
无公共点 4条公切线
无公共点 无公切线
