高中数学人教A版必修二第二章2.2.2 平面与平面平行的判定课件(22张PPT)
文档属性
| 名称 | 高中数学人教A版必修二第二章2.2.2 平面与平面平行的判定课件(22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 204.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 21:01:48 | ||
图片预览




文档简介
平面与平面平行的判定
一:复习回顾:
2.两平面有哪些位置关系?
相交
平行
有公共点
无公共点
1.如何判定直线与平面平行?
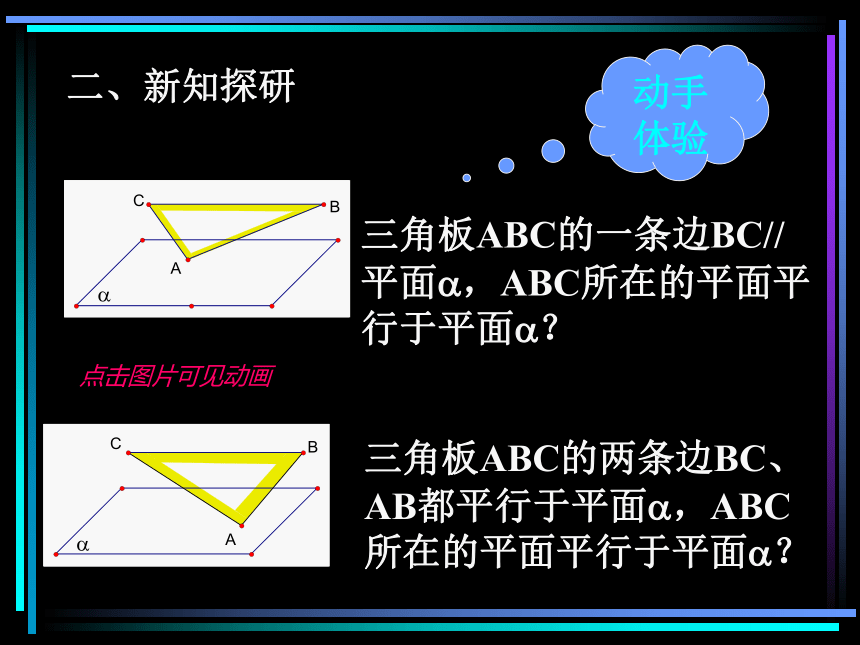
二、新知探研
点击图片可见动画
三角板ABC的一条边BC//平面?,ABC所在的平面平行于平面??
三角板ABC的两条边BC、AB都平行于平面?,ABC所在的平面平行于平面??
动手体验
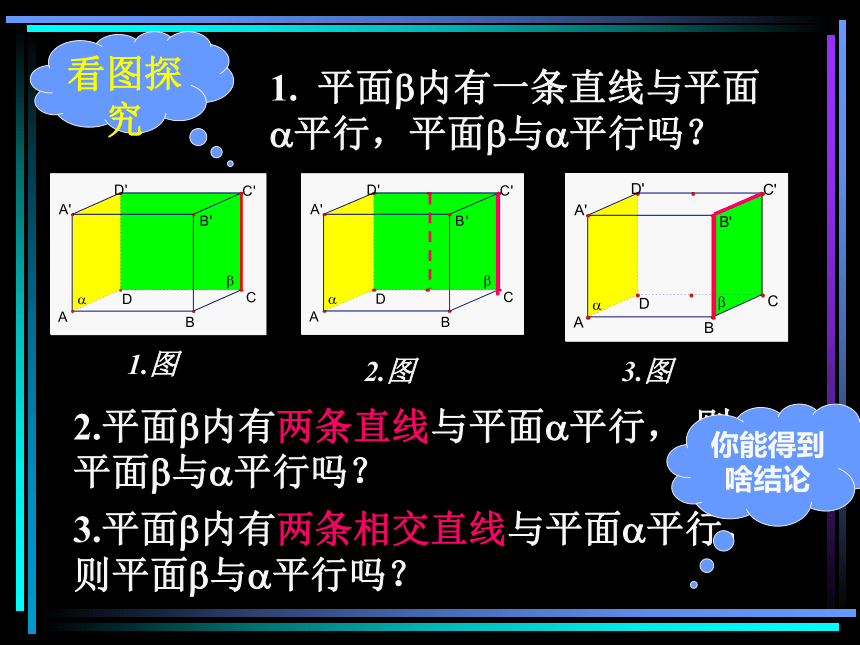
看图探究
1. 平面?内有一条直线与平面?平行,平面?与?平行吗?
2.平面?内有两条直线与平面?平行, 则平面?与?平行吗?
1.图
2.图
3.图
3.平面?内有两条相交直线与平面?平行, 则平面?与?平行吗?
你能得到啥结论
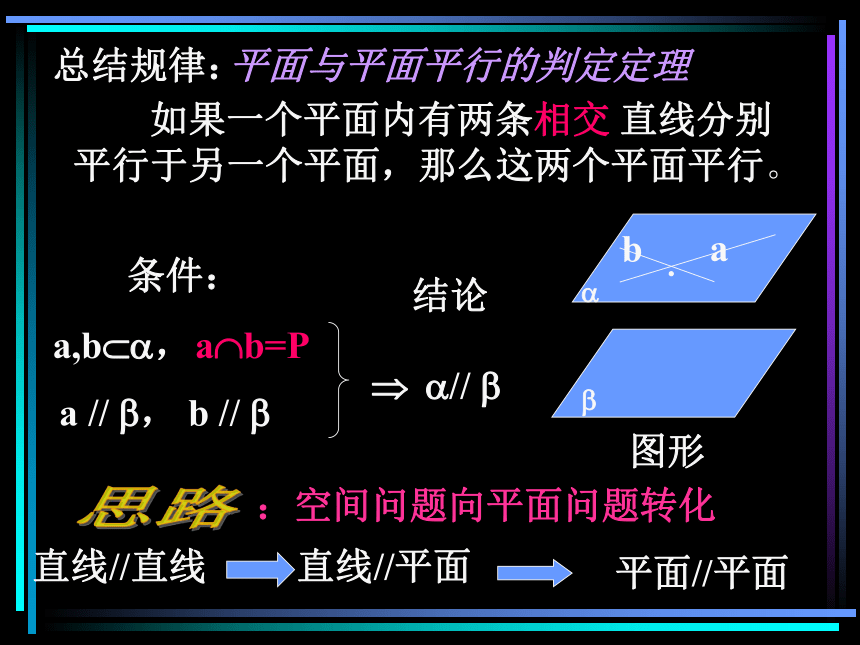
总结规律:
如果一个平面内有两条 直线分别
平行于另一个平面,那么这两个平面平行。
a
b
?
条件:
a,b??,
a?b=P
a // ?,
b // ?
结论
?// ?
图形
?
?
?
直线//平面
平面//平面
思路
相交
直线//直线
:空间问题向平面问题转化
平面与平面平行的判定定理
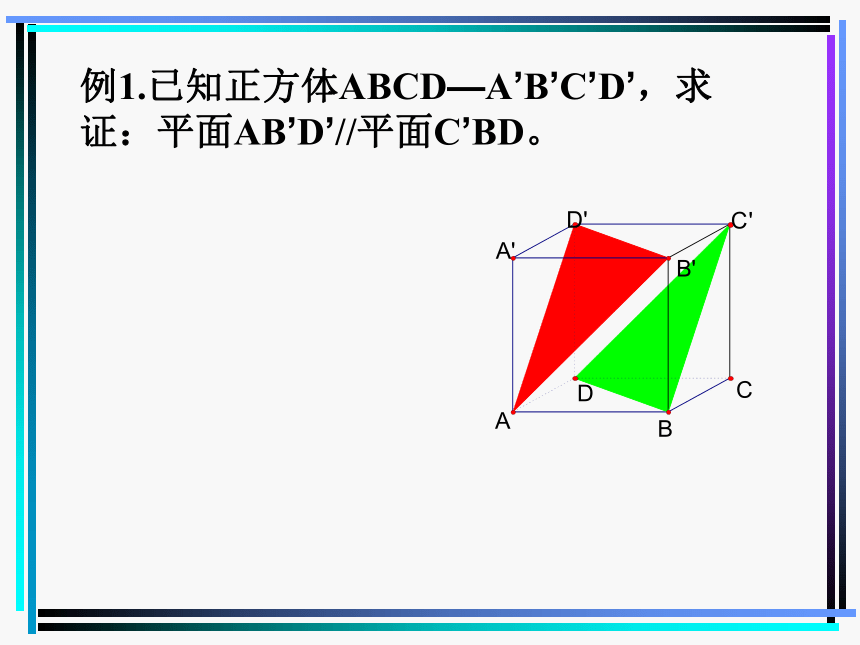
例1.已知正方体ABCD—A’B’C’D’,求证:平面AB’D’//平面C’BD。
判断正误,并说明理由:
平面α内有两条直线平行于另一平面β,
则 α∥β;
平面α内有无数条直线平行于另一平面β,则α∥β;
一个平面内不平行的两条直线都与另一个平面平行,则这两平面平行;
(4) 平面α内的两相交分别平行于另一平面β内的两相交直线,则α∥β
练习与巩固
定理变式:
如果一个平面内的两相交直线分别平行于另一个平面内的两条直线,则这两个平面平行。
推论1:
a
b
m
n
?
?
P
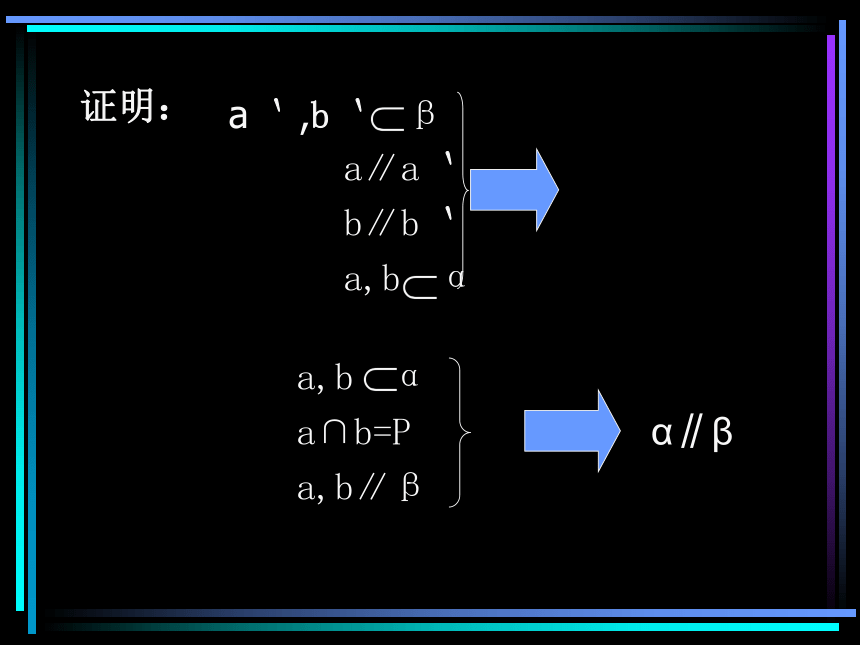
a,b α
a∩b=P
a,b∥β
α∥β
a` ,b` β
a∥a`
b∥b`
a,b α
证明:
例2. 已知ABC-A?B?C?正三棱柱,E、E?分别是AC、A?C?的中点,求证:平面AB?E?//平面BEC ?
A
B
C
E
A?
B?
C?
E?
例题3: 直线
交与点
求证:平面 // 平面
点击图片可以演示动画
四、练习与提高
1.下列命题正确的是
A若
2.已知?,?表示两个平面,同m、n表示两条直线,则使?//?的一个条件是
3.下列命题中正确的是
A、平行于同一直线的两个平面平行
B、平行于同一平面的两个平面平行
C、垂直于同一条直线 的两条直线平行
D、平行于同一个平面的两直线平行
(本题结论可作为判定定理的推论2)
4.已知: 在正方体ABCD-A1B1C1D1中,
E、F分别是CC1、AA1的中点,
求证: 平面BDE//平面B1D1F
A
D1
D
C
B
A1
B1
C1
E
F
G
五、小结
1个定理:
1个思想:
2个变式:
一个平面内不相交的两条直线都 与另一个平面平行,则这两平面平行
平行于同一平面的两个平面平行
转化思想:面//面 线//面
1)
2)
面面平行的判定定理
六、作业
1.下列命题中,正确的是
A 过平面外的一条直线,最多只能作一个
B. 如果有两条直线都和一个平面平行,过这两条直线的平面也和这个平面 平行
平面和这个平面平行
C.过外一点,和这个平面平行的直线所确定
D.一个平面内的两条直线与另一个平面内的两条直线分别平行,则这两个平面平行
的平面,和这个平面平行
2. 直线
交与点
求证:平面 // 平面
3.如图a,b是异面直线,a??,a//?,b//
?,b??,求证:?//?
a
b
?
?
4.如图,正方体ABCD-A?B?C?D?中,
M,N,E,F分别是棱A?B ?,A?D?,
B?C?,C?D?的中点,
求证:平面AMN//平面EFDB
A
A?
B ?
B
C
C ?
D
D ?
N
M
E
F
5.如图,在棱长为2cm的正方体ABCD-A?B?C?D?中,A?B?的中点是P,问过点A?能作与截面PBC?平行的截面吗?若能作出图形,若不能说明理由。
A
B
C
D
A?
B?
C?
D?
P
6.如图空间六边形ABCC?B?A?的六个顶点中没有任何五点共面,每相邻的两边互相垂直,边长均为a,且BC//A?B?,AA?//CC?,求证:平面A?BC?//平面ACB?
A
B
C
A ?
B?
C?
一:复习回顾:
2.两平面有哪些位置关系?
相交
平行
有公共点
无公共点
1.如何判定直线与平面平行?
二、新知探研
点击图片可见动画
三角板ABC的一条边BC//平面?,ABC所在的平面平行于平面??
三角板ABC的两条边BC、AB都平行于平面?,ABC所在的平面平行于平面??
动手体验
看图探究
1. 平面?内有一条直线与平面?平行,平面?与?平行吗?
2.平面?内有两条直线与平面?平行, 则平面?与?平行吗?
1.图
2.图
3.图
3.平面?内有两条相交直线与平面?平行, 则平面?与?平行吗?
你能得到啥结论
总结规律:
如果一个平面内有两条 直线分别
平行于另一个平面,那么这两个平面平行。
a
b
?
条件:
a,b??,
a?b=P
a // ?,
b // ?
结论
?// ?
图形
?
?
?
直线//平面
平面//平面
思路
相交
直线//直线
:空间问题向平面问题转化
平面与平面平行的判定定理
例1.已知正方体ABCD—A’B’C’D’,求证:平面AB’D’//平面C’BD。
判断正误,并说明理由:
平面α内有两条直线平行于另一平面β,
则 α∥β;
平面α内有无数条直线平行于另一平面β,则α∥β;
一个平面内不平行的两条直线都与另一个平面平行,则这两平面平行;
(4) 平面α内的两相交分别平行于另一平面β内的两相交直线,则α∥β
练习与巩固
定理变式:
如果一个平面内的两相交直线分别平行于另一个平面内的两条直线,则这两个平面平行。
推论1:
a
b
m
n
?
?
P
a,b α
a∩b=P
a,b∥β
α∥β
a` ,b` β
a∥a`
b∥b`
a,b α
证明:
例2. 已知ABC-A?B?C?正三棱柱,E、E?分别是AC、A?C?的中点,求证:平面AB?E?//平面BEC ?
A
B
C
E
A?
B?
C?
E?
例题3: 直线
交与点
求证:平面 // 平面
点击图片可以演示动画
四、练习与提高
1.下列命题正确的是
A若
2.已知?,?表示两个平面,同m、n表示两条直线,则使?//?的一个条件是
3.下列命题中正确的是
A、平行于同一直线的两个平面平行
B、平行于同一平面的两个平面平行
C、垂直于同一条直线 的两条直线平行
D、平行于同一个平面的两直线平行
(本题结论可作为判定定理的推论2)
4.已知: 在正方体ABCD-A1B1C1D1中,
E、F分别是CC1、AA1的中点,
求证: 平面BDE//平面B1D1F
A
D1
D
C
B
A1
B1
C1
E
F
G
五、小结
1个定理:
1个思想:
2个变式:
一个平面内不相交的两条直线都 与另一个平面平行,则这两平面平行
平行于同一平面的两个平面平行
转化思想:面//面 线//面
1)
2)
面面平行的判定定理
六、作业
1.下列命题中,正确的是
A 过平面外的一条直线,最多只能作一个
B. 如果有两条直线都和一个平面平行,过这两条直线的平面也和这个平面 平行
平面和这个平面平行
C.过外一点,和这个平面平行的直线所确定
D.一个平面内的两条直线与另一个平面内的两条直线分别平行,则这两个平面平行
的平面,和这个平面平行
2. 直线
交与点
求证:平面 // 平面
3.如图a,b是异面直线,a??,a//?,b//
?,b??,求证:?//?
a
b
?
?
4.如图,正方体ABCD-A?B?C?D?中,
M,N,E,F分别是棱A?B ?,A?D?,
B?C?,C?D?的中点,
求证:平面AMN//平面EFDB
A
A?
B ?
B
C
C ?
D
D ?
N
M
E
F
5.如图,在棱长为2cm的正方体ABCD-A?B?C?D?中,A?B?的中点是P,问过点A?能作与截面PBC?平行的截面吗?若能作出图形,若不能说明理由。
A
B
C
D
A?
B?
C?
D?
P
6.如图空间六边形ABCC?B?A?的六个顶点中没有任何五点共面,每相邻的两边互相垂直,边长均为a,且BC//A?B?,AA?//CC?,求证:平面A?BC?//平面ACB?
A
B
C
A ?
B?
C?
