高中数学人教A版选修2-2:1.3.3函数的最大最小值与导数 课件(20张PPT)
文档属性
| 名称 | 高中数学人教A版选修2-2:1.3.3函数的最大最小值与导数 课件(20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 382.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 00:00:00 | ||
图片预览




文档简介
1.3.3函数的最大(小)值与导数
高二数学 选修2-2
a
b
y=f(x)
x
o
y
y=f(x)
x
o
y
a
b
f '(x)>0
f '(x)<0
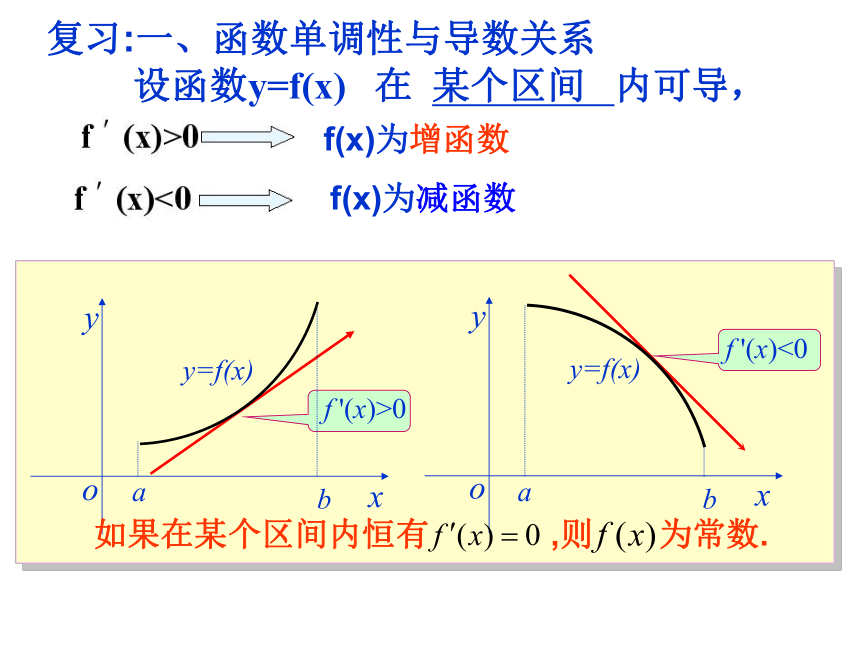
复习:一、函数单调性与导数关系
如果在某个区间内恒有 ,则 为常数.
设函数y=f(x) 在 某个区间 内可导,
f(x)为增函数
f(x)为减函数
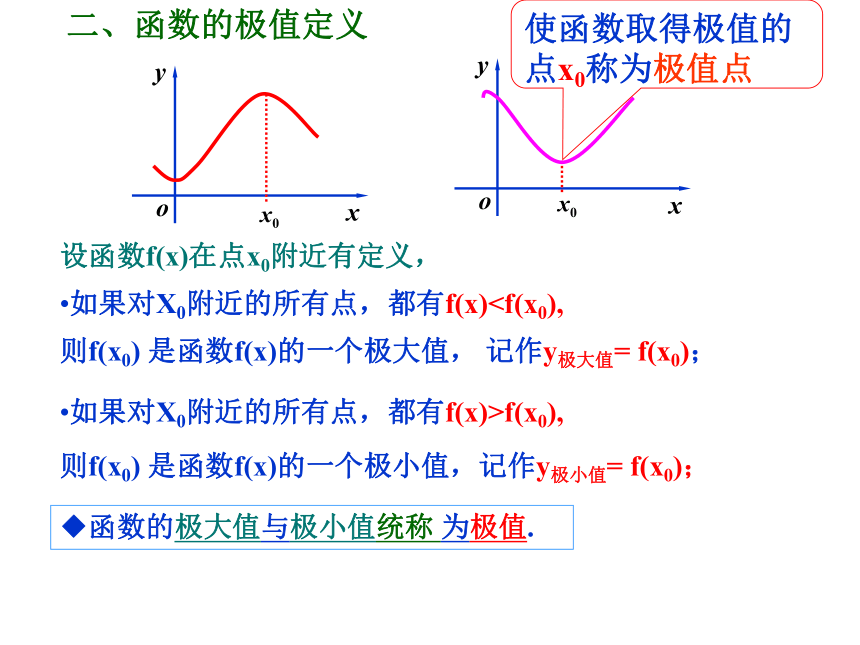
二、函数的极值定义
设函数f(x)在点x0附近有定义,
如果对X0附近的所有点,都有f(x)则f(x0) 是函数f(x)的一个极大值, 记作y极大值= f(x0);
如果对X0附近的所有点,都有f(x)>f(x0),
则f(x0) 是函数f(x)的一个极小值,记作y极小值= f(x0);
◆函数的极大值与极小值统称 为极值.
使函数取得极值的点x0称为极值点
2、求函数极值(极大值,极小值)的一般步骤:
求定义域
求导
求极值点
列表
写极值
左正右负极大值,左负右正极小值
导数的应用之三、求函数最值.
极值是一个局部概念,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小。
在某些问题中,往往关心的是函数在整
个定义域区间上,哪个值最大或最小的问题,这就是我们通常所说的最值问题.
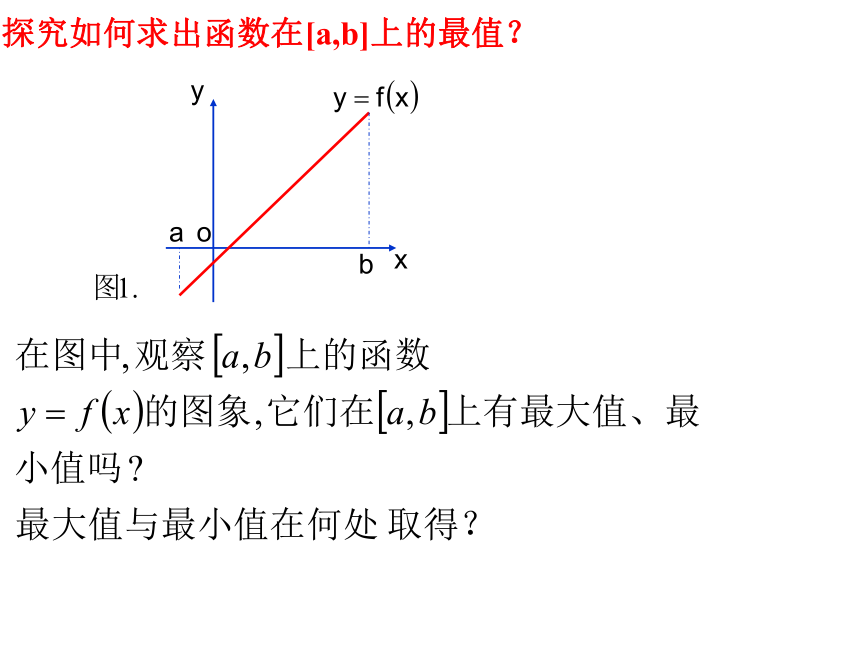
探究如何求出函数在[a,b]上的最值?
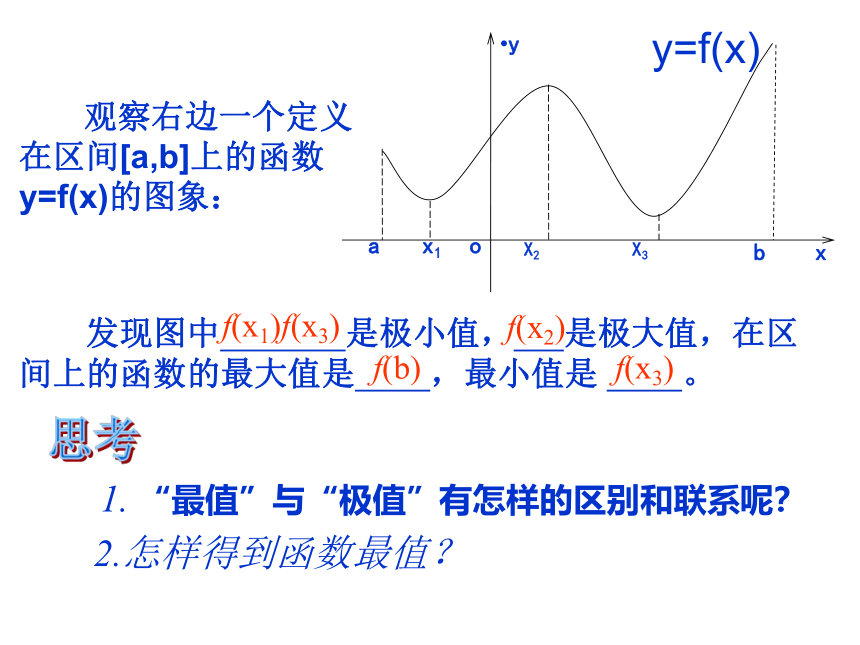
观察右边一个定义在区间[a,b]上的函数y=f(x)的图象:
x
X2
o
a
X3
b
x1
y
y=f(x)
发现图中 是极小值, 是极大值,在区间上的函数的最大值是 ,最小值是 。
f(x2)
f(x1)f(x3)
f(x3)
f(b)
1. “最值”与“极值”有怎样的区别和联系呢?
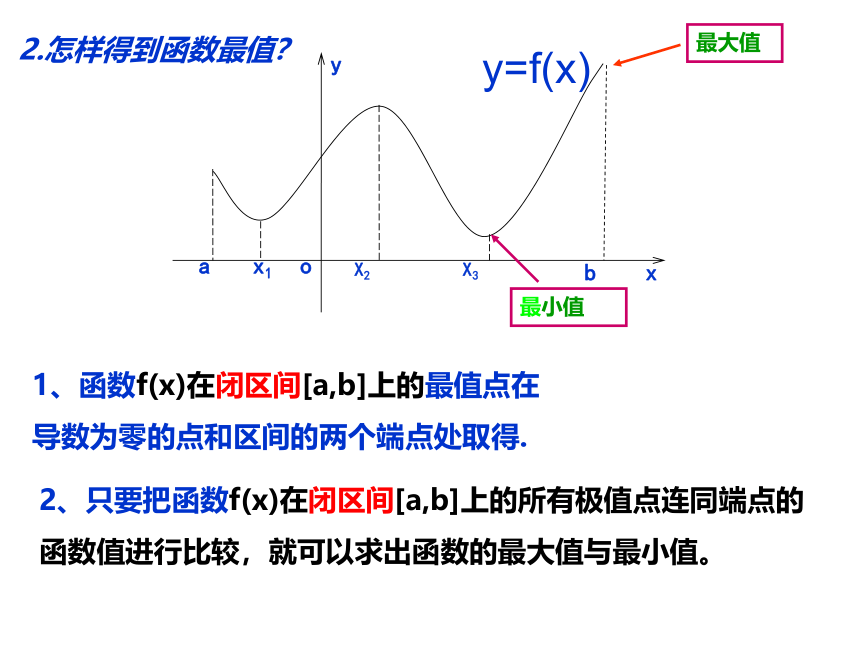
2.怎样得到函数最值?
思考
“最值”与“极值”的有怎样的区别和联系呢?
①、“最值”是整体概念;而“极值”是个局部概念.
②、从个数上看,一个函数在给定的闭区间【a,b】上的最值是唯一的;而极值可能有多个,也可能只有一个,还可能一个都没有;
③、在极值点x0处的导数f′(x0)=0,而最值点不一定,最值有可能在极值点取得,也可能在端点处取得。
2.怎样得到函数最值?
x
X2
o
a
X3
b
x1
y
y=f(x)
1、函数f(x)在闭区间[a,b]上的最值点在
导数为零的点和区间的两个端点处取得.
2、只要把函数f(x)在闭区间[a,b]上的所有极值点连同端点的
函数值进行比较,就可以求出函数的最大值与最小值。
最大值
最小值
导数的应用之三、求函数最值.
(2)将y=f(x)的各极值与f(a)、f(b)(端点处)
比较,其中最大的一个为最大值,最小的
一个为最小值.
求f(x)在闭区间[a,b]上的最值的步骤
(1)求f(x)在区间(a,b)内极值(极大值或极小值)
例1、求函数f(x)= -4x+4在区间[0,3] 内的最大值和最小值
x
(0,2)
2
(2,3)
f'(x)
-
0
+
f(x)
-4/3
2、求函数f(x)=3x-x3 在区间 [-3,3] 内的最大值和最小值
练习
1、变式将区间 [0,3] 改为[-3,4]
求函数的最大值和最小值
f(x)最大值为f(-2)=f(4)=28/3
f(x)最小值为f(2)=-4/3
f(x)最大值为f(1)=2
f(x)最小值为f(-3)=-36
※典型例题
反思:本题是由函数的最值求参数的值:
基本方法最终落脚到比较极值与端点函数值大小上,从而解决问题.
一.函数极值与最值区别与联系二.利用导数求函数最值的方法
课堂小结
求f(x)在[a,b]上的最大值与最小值的步骤如下:
①:求y=f(x)在(a,b)内的极值(极大值与极小值);
②:将函数y=f(x)的各极值与f(a)、f(b)作比较, 其中最大的一个为最大值,最小的一个为最小值.
注意
1) 函数的最值是整体性的概念;
2) 函数的最大值(最小值)唯一;
3) 函数的最值可在端点取得.
总结
4、函数y=x3-3x2,在[-2,4]上的最大值为( )
(A) -4 (B) 0 (C) 16 (D) 20
C
1.
习题答案
练习(第31页)
习题答案
已知a为实数,
(Ⅰ)求导数 ;
(Ⅱ)若 ,求 在[-2,2]上的最大值和最小值;
课后思考
(浙江某年高考文)
课后作业
习题1.3A组 6题 (2) (3)
再见
高二数学 选修2-2
a
b
y=f(x)
x
o
y
y=f(x)
x
o
y
a
b
f '(x)>0
f '(x)<0
复习:一、函数单调性与导数关系
如果在某个区间内恒有 ,则 为常数.
设函数y=f(x) 在 某个区间 内可导,
f(x)为增函数
f(x)为减函数
二、函数的极值定义
设函数f(x)在点x0附近有定义,
如果对X0附近的所有点,都有f(x)
如果对X0附近的所有点,都有f(x)>f(x0),
则f(x0) 是函数f(x)的一个极小值,记作y极小值= f(x0);
◆函数的极大值与极小值统称 为极值.
使函数取得极值的点x0称为极值点
2、求函数极值(极大值,极小值)的一般步骤:
求定义域
求导
求极值点
列表
写极值
左正右负极大值,左负右正极小值
导数的应用之三、求函数最值.
极值是一个局部概念,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小。
在某些问题中,往往关心的是函数在整
个定义域区间上,哪个值最大或最小的问题,这就是我们通常所说的最值问题.
探究如何求出函数在[a,b]上的最值?
观察右边一个定义在区间[a,b]上的函数y=f(x)的图象:
x
X2
o
a
X3
b
x1
y
y=f(x)
发现图中 是极小值, 是极大值,在区间上的函数的最大值是 ,最小值是 。
f(x2)
f(x1)f(x3)
f(x3)
f(b)
1. “最值”与“极值”有怎样的区别和联系呢?
2.怎样得到函数最值?
思考
“最值”与“极值”的有怎样的区别和联系呢?
①、“最值”是整体概念;而“极值”是个局部概念.
②、从个数上看,一个函数在给定的闭区间【a,b】上的最值是唯一的;而极值可能有多个,也可能只有一个,还可能一个都没有;
③、在极值点x0处的导数f′(x0)=0,而最值点不一定,最值有可能在极值点取得,也可能在端点处取得。
2.怎样得到函数最值?
x
X2
o
a
X3
b
x1
y
y=f(x)
1、函数f(x)在闭区间[a,b]上的最值点在
导数为零的点和区间的两个端点处取得.
2、只要把函数f(x)在闭区间[a,b]上的所有极值点连同端点的
函数值进行比较,就可以求出函数的最大值与最小值。
最大值
最小值
导数的应用之三、求函数最值.
(2)将y=f(x)的各极值与f(a)、f(b)(端点处)
比较,其中最大的一个为最大值,最小的
一个为最小值.
求f(x)在闭区间[a,b]上的最值的步骤
(1)求f(x)在区间(a,b)内极值(极大值或极小值)
例1、求函数f(x)= -4x+4在区间[0,3] 内的最大值和最小值
x
(0,2)
2
(2,3)
f'(x)
-
0
+
f(x)
-4/3
2、求函数f(x)=3x-x3 在区间 [-3,3] 内的最大值和最小值
练习
1、变式将区间 [0,3] 改为[-3,4]
求函数的最大值和最小值
f(x)最大值为f(-2)=f(4)=28/3
f(x)最小值为f(2)=-4/3
f(x)最大值为f(1)=2
f(x)最小值为f(-3)=-36
※典型例题
反思:本题是由函数的最值求参数的值:
基本方法最终落脚到比较极值与端点函数值大小上,从而解决问题.
一.函数极值与最值区别与联系二.利用导数求函数最值的方法
课堂小结
求f(x)在[a,b]上的最大值与最小值的步骤如下:
①:求y=f(x)在(a,b)内的极值(极大值与极小值);
②:将函数y=f(x)的各极值与f(a)、f(b)作比较, 其中最大的一个为最大值,最小的一个为最小值.
注意
1) 函数的最值是整体性的概念;
2) 函数的最大值(最小值)唯一;
3) 函数的最值可在端点取得.
总结
4、函数y=x3-3x2,在[-2,4]上的最大值为( )
(A) -4 (B) 0 (C) 16 (D) 20
C
1.
习题答案
练习(第31页)
习题答案
已知a为实数,
(Ⅰ)求导数 ;
(Ⅱ)若 ,求 在[-2,2]上的最大值和最小值;
课后思考
(浙江某年高考文)
课后作业
习题1.3A组 6题 (2) (3)
再见
