沪教版(上海)数学高一下册-5.4 两角和与差的正弦、余弦、正切公式(一) 课件(15张PPT)
文档属性
| 名称 | 沪教版(上海)数学高一下册-5.4 两角和与差的正弦、余弦、正切公式(一) 课件(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 174.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 00:00:00 | ||
图片预览





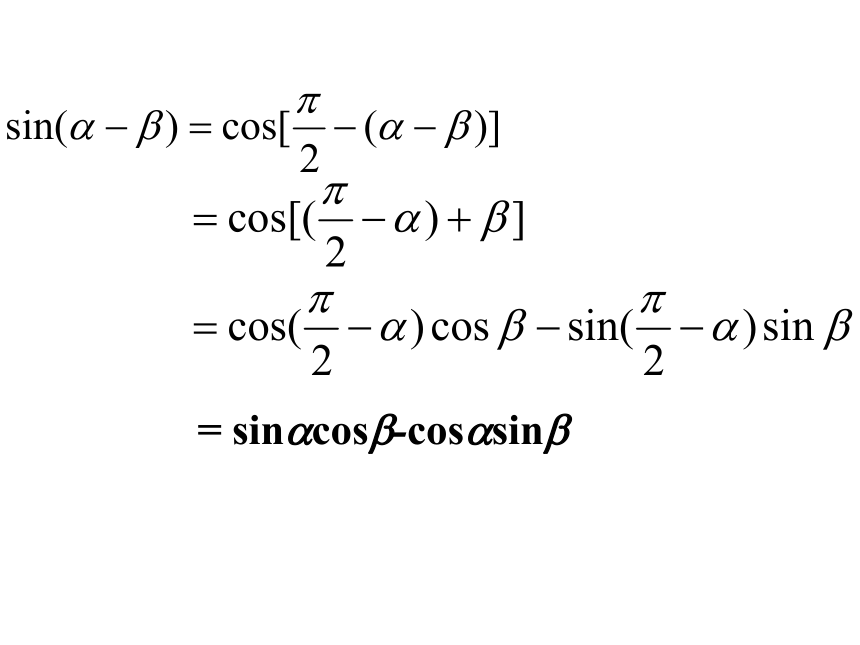
文档简介
两角和与差的正弦、余弦、正切公式(一)
1.2 两角差的余弦公式
( C(?-?) )
cos?cos?+sin?sin?
公
式
五
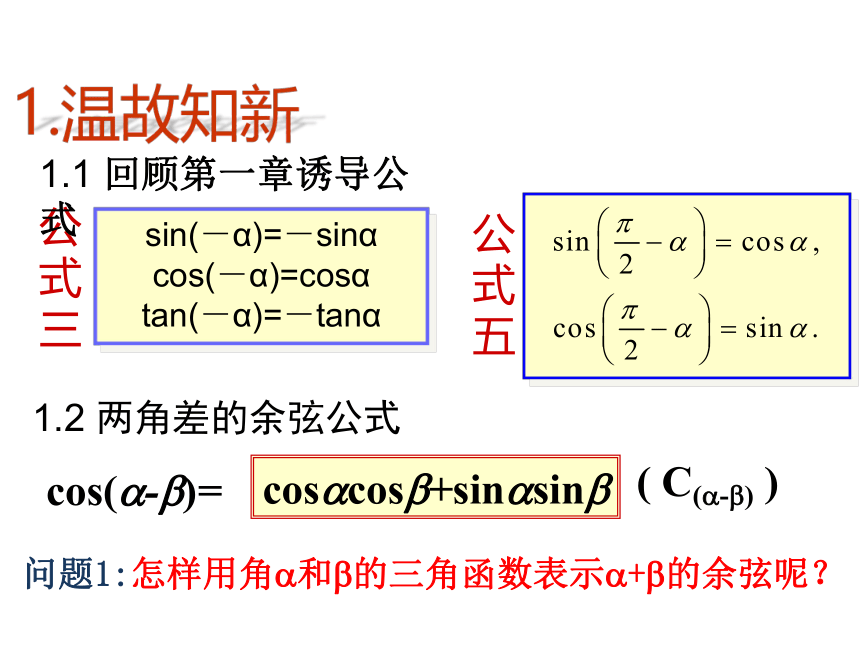
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
公
式
三
1.温故知新
1.1 回顾第一章诱导公式
问题1:怎样用角?和?的三角函数表示?+?的余弦呢?
cos(?-?)=
提示:由两角差的余弦公式探究两角和的余弦公式
思路1:从两角加法与减法之间的联系来探究
=cos?cos(-?)+sin?sin(-?)
= cos?cos?-sin?sin?
? +? =
? - ( - ? )
cos(?+?) =
cos[?-(-?)]
问题1:怎样用角?和?的三角函数表示?+?的余弦呢?
cos(?+?) = cos?cos?-sin?sin?
2.两角和的余弦公式
( C(?+?) )
课后思考:
思路2:从角β是一个任意角来探究(即换元思想)
问题2:怎样用角α和角β的三角函数表示角 α+β和 角α-β的正弦呢?
提示:利用诱导公式五(或六)可以实现正弦,余弦的互化
=sin?cos?+cos?sin?
(S(?+?))
3.两角和的正弦公式
= sin?cos?-cos?sin?
4.两角差的正弦公式
(S(?-?))
(换元思想:也可在S(?+?)用- ?代?得出)
( C(?-?) )
( C(?+?) )
cos(?-?)= cos?cos?+sin?sin?
cos(?+?)= cos?cos?-sin?sin?
( S(?+?) )
( S(?-?) )
sin(?+?)= sin?cos?+cos?sin?
sin(? -?)= sin?cos?-cos?sin?
注意公式的结构特征和符号的规律:
对于公式C(α-β)、C(α+β)可记为“同名相乘,符号反”
对于公式S(α+β)、S(α-β)可记为“异名相乘,符号同”
比一比
5.例题讲解
解:
?是第四象限角,得
例1.
求下列各式的值
6.课堂练习
7.两角和与差的正弦、余弦、正切公式的内在联系
C(?-?)
C(?+?)
-?代?
S(?-?)
S(?+?)
-?代?
T(?+?)
相除
T(?-?)
相除
8.小结
( C(?-?) )
( C(?+?) )
cos(?-?)= cos?cos?+sin?sin?
cos(?+?)= cos?cos?-sin?sin?
( S(?+?) )
( S(?-?) )
sin(?+?)= sin?cos?+cos?sin?
sin(?-?)= sin?cos?-cos?sin?
两角和与差的正弦、余弦、正切公式
1.注意公式的结构特征和符号的规律:
对于公式C(α-β)、C(α+β)可记为“同名相乘,符号反”
对于公式S(α+β)、S(α-β)可记为“异名相乘,符号同”
2.使用公式时,不仅要会正用,还要能够逆用公式。
温馨提示:
作业:
1.教科书
2.思考:如何用?和?的正弦值表示?+?和?-?的正切值呢?
1.2 两角差的余弦公式
( C(?-?) )
cos?cos?+sin?sin?
公
式
五
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
公
式
三
1.温故知新
1.1 回顾第一章诱导公式
问题1:怎样用角?和?的三角函数表示?+?的余弦呢?
cos(?-?)=
提示:由两角差的余弦公式探究两角和的余弦公式
思路1:从两角加法与减法之间的联系来探究
=cos?cos(-?)+sin?sin(-?)
= cos?cos?-sin?sin?
? +? =
? - ( - ? )
cos(?+?) =
cos[?-(-?)]
问题1:怎样用角?和?的三角函数表示?+?的余弦呢?
cos(?+?) = cos?cos?-sin?sin?
2.两角和的余弦公式
( C(?+?) )
课后思考:
思路2:从角β是一个任意角来探究(即换元思想)
问题2:怎样用角α和角β的三角函数表示角 α+β和 角α-β的正弦呢?
提示:利用诱导公式五(或六)可以实现正弦,余弦的互化
=sin?cos?+cos?sin?
(S(?+?))
3.两角和的正弦公式
= sin?cos?-cos?sin?
4.两角差的正弦公式
(S(?-?))
(换元思想:也可在S(?+?)用- ?代?得出)
( C(?-?) )
( C(?+?) )
cos(?-?)= cos?cos?+sin?sin?
cos(?+?)= cos?cos?-sin?sin?
( S(?+?) )
( S(?-?) )
sin(?+?)= sin?cos?+cos?sin?
sin(? -?)= sin?cos?-cos?sin?
注意公式的结构特征和符号的规律:
对于公式C(α-β)、C(α+β)可记为“同名相乘,符号反”
对于公式S(α+β)、S(α-β)可记为“异名相乘,符号同”
比一比
5.例题讲解
解:
?是第四象限角,得
例1.
求下列各式的值
6.课堂练习
7.两角和与差的正弦、余弦、正切公式的内在联系
C(?-?)
C(?+?)
-?代?
S(?-?)
S(?+?)
-?代?
T(?+?)
相除
T(?-?)
相除
8.小结
( C(?-?) )
( C(?+?) )
cos(?-?)= cos?cos?+sin?sin?
cos(?+?)= cos?cos?-sin?sin?
( S(?+?) )
( S(?-?) )
sin(?+?)= sin?cos?+cos?sin?
sin(?-?)= sin?cos?-cos?sin?
两角和与差的正弦、余弦、正切公式
1.注意公式的结构特征和符号的规律:
对于公式C(α-β)、C(α+β)可记为“同名相乘,符号反”
对于公式S(α+β)、S(α-β)可记为“异名相乘,符号同”
2.使用公式时,不仅要会正用,还要能够逆用公式。
温馨提示:
作业:
1.教科书
2.思考:如何用?和?的正弦值表示?+?和?-?的正切值呢?
