高中数学人教A版必修二:2.3.2 平面与平面垂直的判定 课件(24张PPT)
文档属性
| 名称 | 高中数学人教A版必修二:2.3.2 平面与平面垂直的判定 课件(24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 610.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 00:00:00 | ||
图片预览

文档简介
平面与平面垂直的判定
*
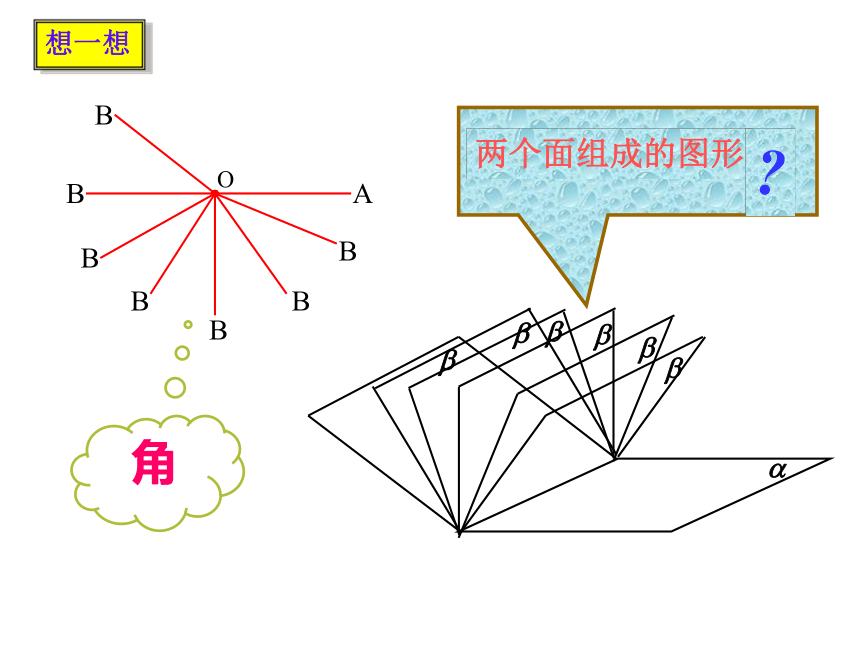
想一想
?
?
?
?
?
?
A
O
B
B
B
B
B
B
B
?
角
两个面组成的图形
?
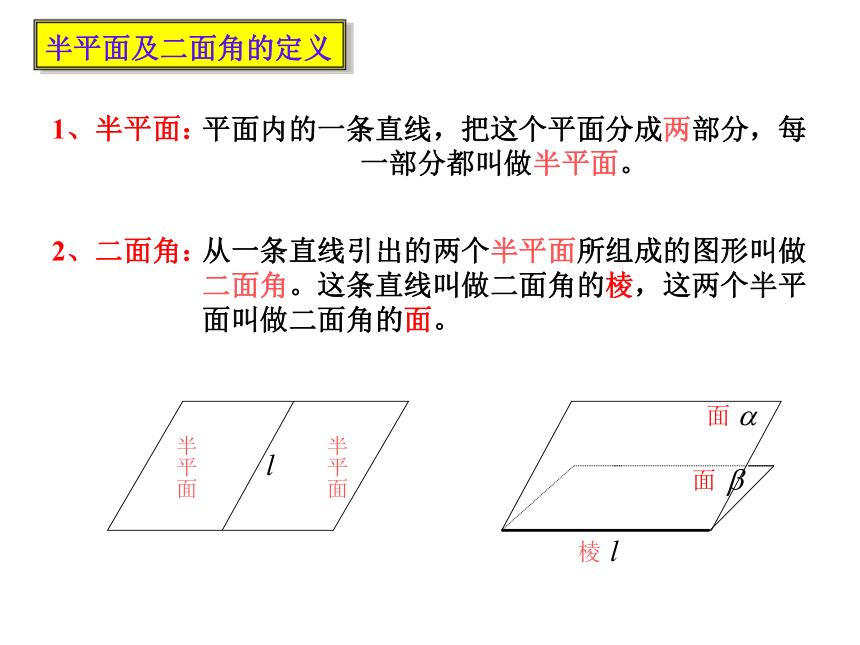
平面内的一条直线,把这个平面分成两部分,每
一部分都叫做半平面。
从一条直线引出的两个半平面所组成的图形叫做
二面角。这条直线叫做二面角的棱,这两个半平
面叫做二面角的面。
1、半平面:
2、二面角:
半平面及二面角的定义
棱
面
面
半平面
半平面
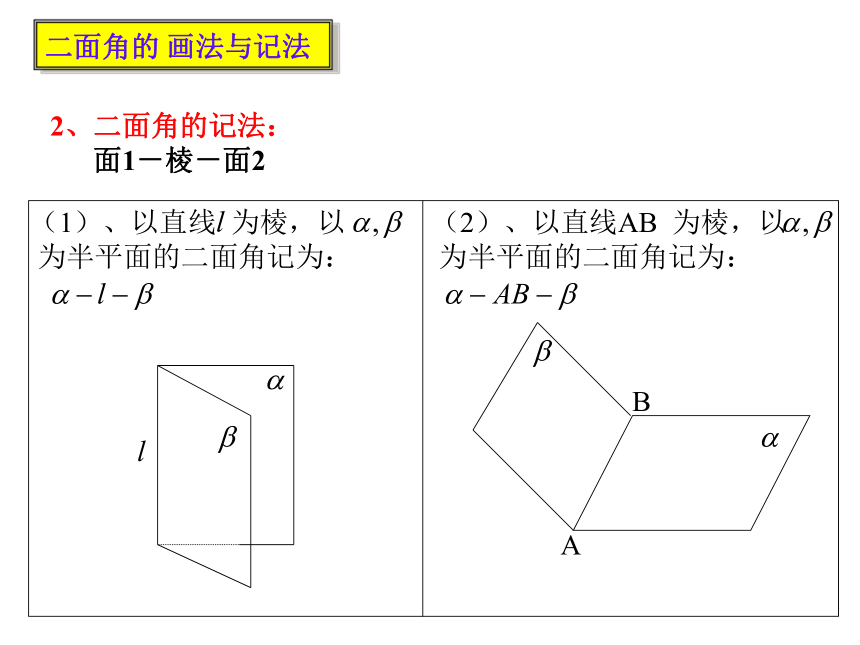
2、二面角的记法:
面1-棱-面2
(1)、以直线 为棱,以
为半平面的二面角记为:
(2)、以直线AB 为棱,以
为半平面的二面角记为:
A
B
二面角的 画法与记法
l
?
?
A
B
?
?
二面角?-AB- ?
?
?
l
二面角?- l- ?
二面角C-AB- D
A
B
C
D
5
O
B
A
∠AOB
?
?
?
?
?
?
?
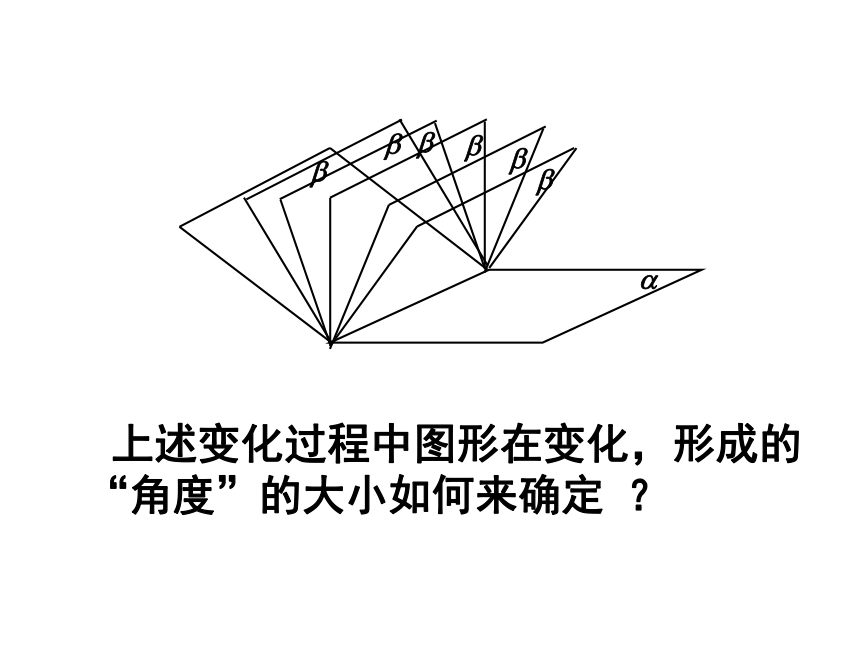
上述变化过程中图形在变化,形成的“角度”的大小如何来确定 ?
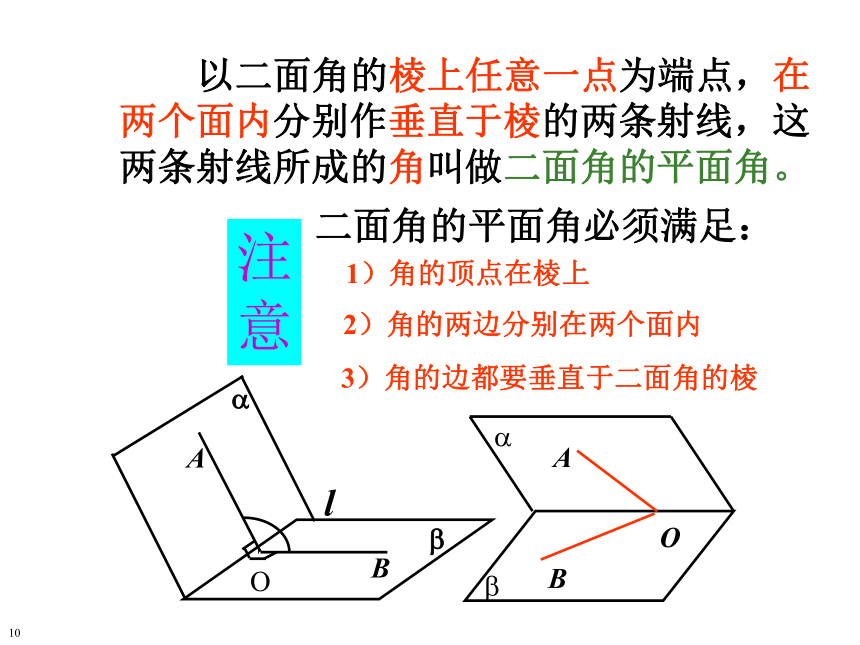
注意
二面角的平面角必须满足:
3)角的边都要垂直于二面角的棱
1)角的顶点在棱上
2)角的两边分别在两个面内
以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
10
?
?
l
O
A
B
?
?
A
O
B
1、二面角的平面角:
以二面角的棱上任意一点为端点,在两个面上分别引垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
==
?
等角定理:如果一个角的两边和另
一个角的两边分别平行,并且方向相
同,那么这两个角相等。)
注:(1)二面角的平面角与点的位置
无关,只与二面角的张角大小有关。
(2)二面角是用它的平面角来度
量的,一个二面角的平面角多大,就
说这个二面角是多少度的二面角。
(3)平面角是直角的二面角叫做
直二面角。
(4)二面角的取值范围一般规定
为(0,π)。
二面角的 平面角的定义、范围及作法
角
B
A
O
边
边
顶点
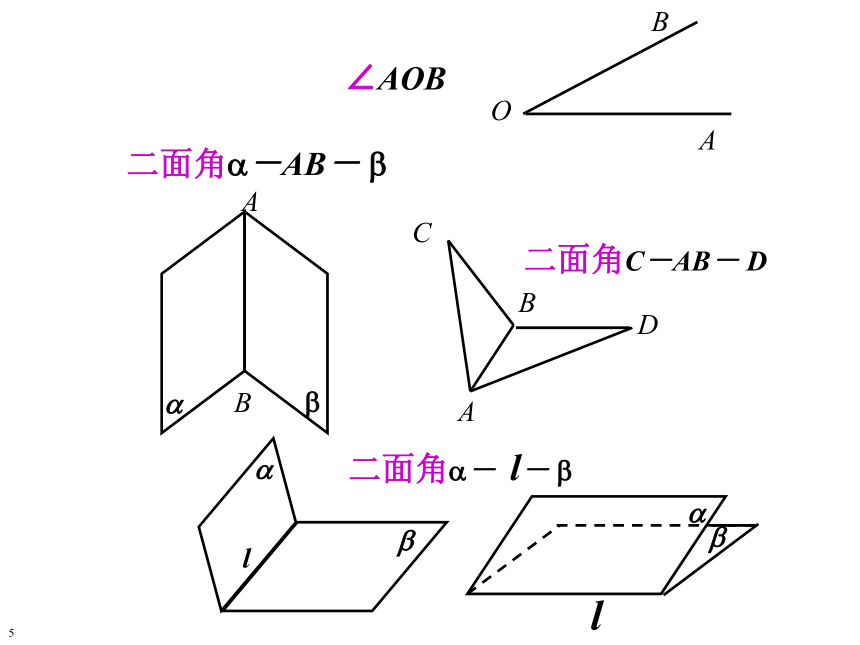
从一点出发的两条射线所组成的图形叫做角。
定义
构成
边—点—边
(顶点)
表示法
∠AOB
二面角
A
B
面
面
棱
a
?
?
从一条直线出发的两个半平面所组成的图形叫做二面角。
面—直线—面
(棱)
二面角?—l—?
或二面角?—AB—?
图形
角与二面角的比较
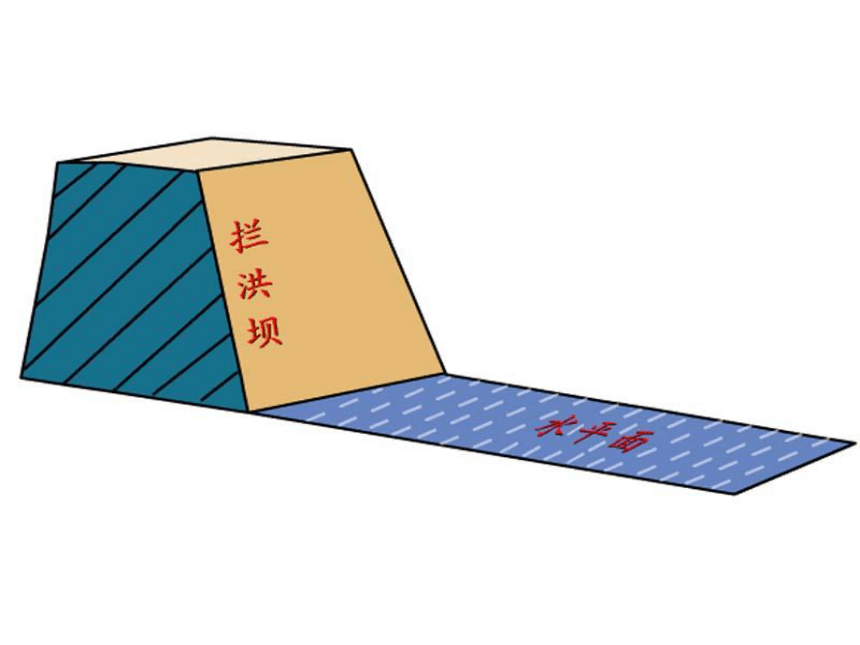
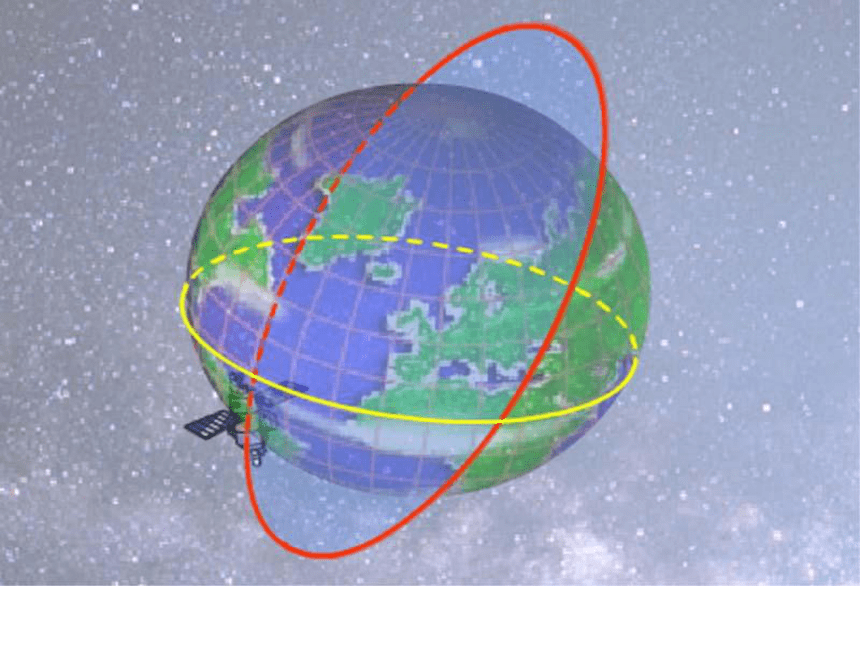
两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面相互垂直.
记作:
三、两个平面互相垂直的意义
问题:
如何检测所砌的墙面和地面是否垂直?
问题:
如何检测所砌的墙面和地面是否垂直?
如果一个平面经过了另一个平面的一条垂线,那么这两个平面互相垂直.
猜想:
如果一个平面经过了另一个平面的一条垂线,那么这两个平面互相垂直。
已知:AB⊥β,AB α
求证:α⊥β.
∪
证明:
α
β
C
D
A
B
E
在平面β内过B点作直线BE⊥CD,则∠ABE就是二面角α--CD--β的平面角,
设α∩β=CD,则B∈CD.
∪
∵AB⊥β,CD β,∴AB⊥CD.
∪
∵AB⊥β,BE β,
∴AB⊥BE. ∴二面角α--CD--β是
直二面角,∴α⊥β.
两个平面垂直的判定定理:
线线垂直
线面垂直
面面垂直
如果一个平面经过了另一个平面的一条垂线,那么这两个平面互相垂直.
证明面面垂直的本质和关键是什么?
本质:线面垂直 面面垂直
关键:找垂直平面的线
课堂练习:
1.如果平面α内有一条直线垂直于平面β内的一条 直线,则α⊥β.( )
3. 如果平面α内的一条直线垂直于平面β内的两条
相交直线, 则α⊥β.( )
一、判断:
×
×
√
2.如果平面α内有一条直线垂直于平面β内的两条
直线,则α⊥β.( )
1.过平面α的一条垂线可作_____个平面
与平面α垂直.
2.过一点可作_____个平面与已知平面垂
直.
二、填空题:
3.过平面α的一条斜线,可作____个平
面与平面α垂直.
4.过平面α的一条平行线可作____个平
面与α垂直.
一
无数
无数
一
A
B
C
D
A1
B1
C1
D1
例1:在正方体ABCD-A1B1C1D1中,
求证: .
例2:如图,AB是圆O的直径,PA垂直于圆O所在
的平面,C是圆周上不同于A,B的任意一点,求证:
P
A
B
C
O
练习1:如图:在Rt△ABC中,∠B=900 ,P为△ABC所在平面外一点,PA⊥平面ABC,问:四面体PABC中有几个直角三角形?并证明之.
P
A
B
C
答案:四个面都是直角三角形
A
B
C
D
E
作业
教材P69 练习
P73习题 A组1、2
*
想一想
?
?
?
?
?
?
A
O
B
B
B
B
B
B
B
?
角
两个面组成的图形
?
平面内的一条直线,把这个平面分成两部分,每
一部分都叫做半平面。
从一条直线引出的两个半平面所组成的图形叫做
二面角。这条直线叫做二面角的棱,这两个半平
面叫做二面角的面。
1、半平面:
2、二面角:
半平面及二面角的定义
棱
面
面
半平面
半平面
2、二面角的记法:
面1-棱-面2
(1)、以直线 为棱,以
为半平面的二面角记为:
(2)、以直线AB 为棱,以
为半平面的二面角记为:
A
B
二面角的 画法与记法
l
?
?
A
B
?
?
二面角?-AB- ?
?
?
l
二面角?- l- ?
二面角C-AB- D
A
B
C
D
5
O
B
A
∠AOB
?
?
?
?
?
?
?
上述变化过程中图形在变化,形成的“角度”的大小如何来确定 ?
注意
二面角的平面角必须满足:
3)角的边都要垂直于二面角的棱
1)角的顶点在棱上
2)角的两边分别在两个面内
以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
10
?
?
l
O
A
B
?
?
A
O
B
1、二面角的平面角:
以二面角的棱上任意一点为端点,在两个面上分别引垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
==
?
等角定理:如果一个角的两边和另
一个角的两边分别平行,并且方向相
同,那么这两个角相等。)
注:(1)二面角的平面角与点的位置
无关,只与二面角的张角大小有关。
(2)二面角是用它的平面角来度
量的,一个二面角的平面角多大,就
说这个二面角是多少度的二面角。
(3)平面角是直角的二面角叫做
直二面角。
(4)二面角的取值范围一般规定
为(0,π)。
二面角的 平面角的定义、范围及作法
角
B
A
O
边
边
顶点
从一点出发的两条射线所组成的图形叫做角。
定义
构成
边—点—边
(顶点)
表示法
∠AOB
二面角
A
B
面
面
棱
a
?
?
从一条直线出发的两个半平面所组成的图形叫做二面角。
面—直线—面
(棱)
二面角?—l—?
或二面角?—AB—?
图形
角与二面角的比较
两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面相互垂直.
记作:
三、两个平面互相垂直的意义
问题:
如何检测所砌的墙面和地面是否垂直?
问题:
如何检测所砌的墙面和地面是否垂直?
如果一个平面经过了另一个平面的一条垂线,那么这两个平面互相垂直.
猜想:
如果一个平面经过了另一个平面的一条垂线,那么这两个平面互相垂直。
已知:AB⊥β,AB α
求证:α⊥β.
∪
证明:
α
β
C
D
A
B
E
在平面β内过B点作直线BE⊥CD,则∠ABE就是二面角α--CD--β的平面角,
设α∩β=CD,则B∈CD.
∪
∵AB⊥β,CD β,∴AB⊥CD.
∪
∵AB⊥β,BE β,
∴AB⊥BE. ∴二面角α--CD--β是
直二面角,∴α⊥β.
两个平面垂直的判定定理:
线线垂直
线面垂直
面面垂直
如果一个平面经过了另一个平面的一条垂线,那么这两个平面互相垂直.
证明面面垂直的本质和关键是什么?
本质:线面垂直 面面垂直
关键:找垂直平面的线
课堂练习:
1.如果平面α内有一条直线垂直于平面β内的一条 直线,则α⊥β.( )
3. 如果平面α内的一条直线垂直于平面β内的两条
相交直线, 则α⊥β.( )
一、判断:
×
×
√
2.如果平面α内有一条直线垂直于平面β内的两条
直线,则α⊥β.( )
1.过平面α的一条垂线可作_____个平面
与平面α垂直.
2.过一点可作_____个平面与已知平面垂
直.
二、填空题:
3.过平面α的一条斜线,可作____个平
面与平面α垂直.
4.过平面α的一条平行线可作____个平
面与α垂直.
一
无数
无数
一
A
B
C
D
A1
B1
C1
D1
例1:在正方体ABCD-A1B1C1D1中,
求证: .
例2:如图,AB是圆O的直径,PA垂直于圆O所在
的平面,C是圆周上不同于A,B的任意一点,求证:
P
A
B
C
O
练习1:如图:在Rt△ABC中,∠B=900 ,P为△ABC所在平面外一点,PA⊥平面ABC,问:四面体PABC中有几个直角三角形?并证明之.
P
A
B
C
答案:四个面都是直角三角形
A
B
C
D
E
作业
教材P69 练习
P73习题 A组1、2
