人教版九年级数学下册第 二十八章复习 锐角三角函数教案
文档属性
| 名称 | 人教版九年级数学下册第 二十八章复习 锐角三角函数教案 |  | |
| 格式 | zip | ||
| 文件大小 | 339.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 06:36:36 | ||
图片预览



文档简介
学员编号:
年
级:
课时数:
第
次课
学员姓名:
辅导科目:
学科教师:
班主任:
授课日期及时段
年
月
日
时
分
——
时
分
授课主题
锐角三角函数
教学目标
(1)通过实例认识直角三角形的边角关系,即锐角三角函数(sinA,cosA,tanA),知道30°,45°,60°角的三角函数值.?
(2)会使用计算器由已知锐角求它的三角函数值,由已知三角函数值会求它的对应的锐角.?
(3)运用三角函数解决与直角三角形有关的简单的实际问题.?
(4)能综合运用直角三角形的勾股定理与边角关系解决简单的实际问题
重点难点
重点:解直角三角形及其应用?
难点:解直角三角形及其应用?
教学内容
一、导入
考向分析
结合近几年中考试题分析,锐角三角函数的内容考查主要有以下特点:
1.命题方式为锐角三角函数的定义、性质的应用、特殊角三角函数值的求法,
运用锐角三角函数解决与直角三角形有关的实际问题.
题型有选择题、填空题、解答题,多以中、低档题出现.
2.命题的热点为根据题中给出的信息构建图形,建立数学模型,
然后用解直角三角形的知识解决问题
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
二、知识梳理+经典例题
知识点一:锐角三角函数的概念与性质
1.锐角三角函数的概念:
在Rt△ABC中,∠C是直角,∠A、∠B、∠C的对边分别是a,b,c,如图.
(1)sinA=
=
(2)cosA=
=
(3)tanA=
=
锐角A的正弦、余弦、正切都叫做∠A的 .?
?特别提示:(1)当∠A为锐角时,00.
(2)锐角A的正弦、正切值均随着角度的增大而增大,余弦值随着角度的增大而减小.
2.锐角三角函数的性质:
(1)若∠A为锐角,则有sin(90°-A)= ,
cos(90°-A)= ?
(2)同角三角函数的关系:
①平方关系:sin2A+cos2A=
②商数关系:
=
例1在Rt△ABC中,∠C=90°,AB=8,cosB=,则BC的长为( )
A.4 B.
C.
D.
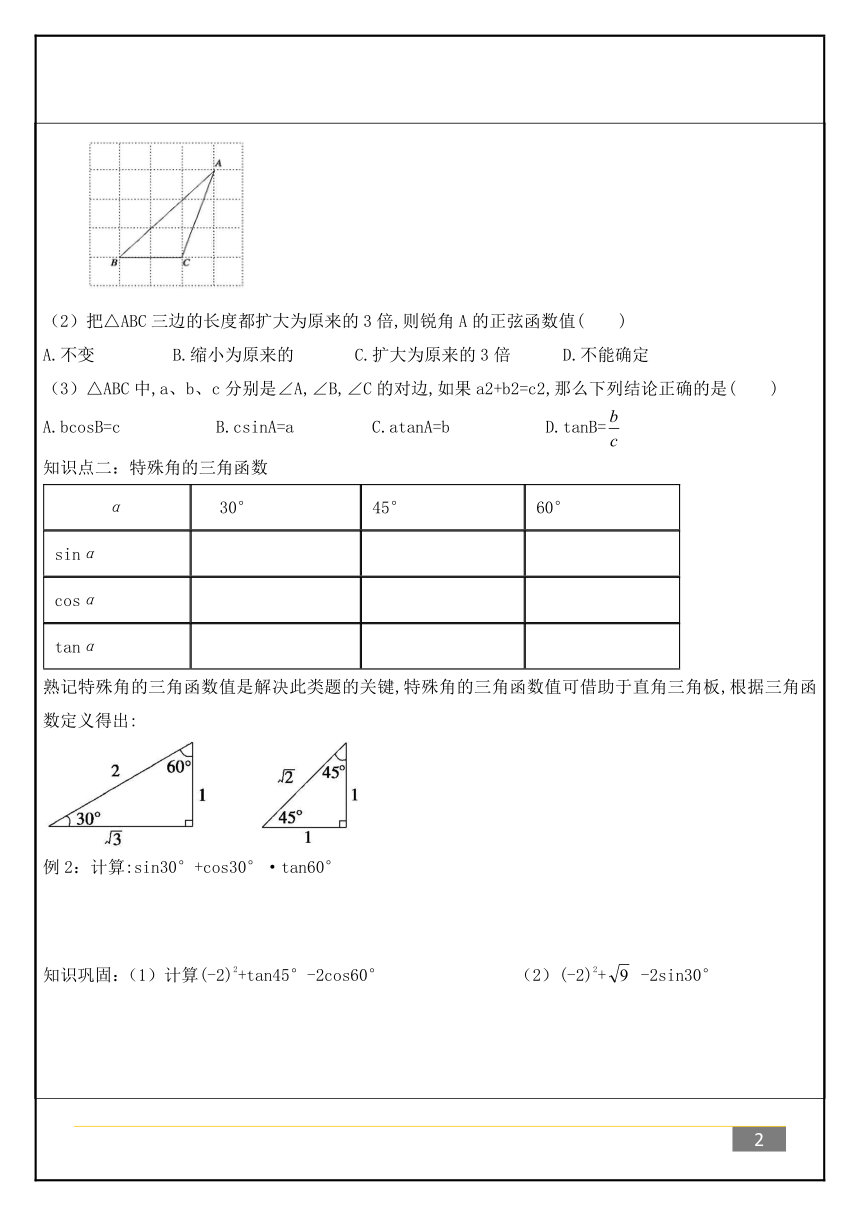
知识巩固:(1)如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( )
A.
B.
C.
D.
(2)把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦函数值( )
A.不变
B.缩小为原来的
C.扩大为原来的3倍
D.不能确定
(3)△ABC中,a、b、c分别是∠A,∠B,∠C的对边,如果a2+b2=c2,那么下列结论正确的是( )
A.bcosB=c
B.csinA=a
C.atanA=b
D.tanB=
知识点二:特殊角的三角函数
???α? 30°?45°60°sinαcosαtanα
熟记特殊角的三角函数值是解决此类题的关键,特殊角的三角函数值可借助于直角三角板,根据三角函数定义得出:
例2:计算:sin30°+cos30°·tan60°
知识巩固:(1)计算(-2)2+tan45°-2cos60°
(2)(-2)2+
-2sin30°
知识点三:解直角三角形
1.直角三角形中,除直角外,一共有五个元素,即
和
.在直角三角形中,由已知元素求 元素的过程,就是解直角三角形.
2.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边.
在解直角三角形的过程中,常用的边角关系:
(1)三边之间的关系: ;?
(2)两锐角之间的关系: ;?
(3)边角之间的关系:sinA=
,sinB=
,cosA=
,
cosB=
,tanA=
,tanB=
解直角三角形的几种类型如下:
1.已知一条直角边和一个锐角(如a,∠A),其解法为:∠B=90°-∠A,c=
,b=
(或b=
);
2.已知斜边和一个锐角(如c,∠A),其解法为:∠B=90°-∠A,a=c·sinA,b=c·cosA(或b=
);
3.已知两直角边(如a,b),其解法为:c=,由tanA=
得∠A,∠B=90°-∠A;
4.已知斜边和一直角边(如c,a),其解法为:b=
,由sinA=,求出∠A,∠B=90°-∠A.
例3:如图,在△ABC中,∠B=45°,∠C=60°,AB=8,求AC.
知识巩固:(1)如图,小亮在太阳光线与地面成35°角时,测得树AB在地面上的影长BC=18
m,则树高AB约为
m(结果精确到0.1
m).
(2)为响应节能环保号召,小明家打算安装一台太阳能发电装置,已知当地安装电池板的最佳角度为54°.如图,按最佳角度安装,若斜杆AB长为1.50
m,则垂直于地面的竖杆AC长应为 m.
知识点四:解直角三角形的应用
1.解直角三角形的应用实际上是将实际问题通过图形使之转化到 中,用锐角三角函数、代数与几何知识综合求解.?
2.仰角和俯角:如图,在同一铅垂面内视线和水平线间的夹角,视线在水平线上方的叫做 ,在水平线下方的叫做 .?
3.坡度(坡比)、坡角:通常把坡面的 和 的比叫坡度(或叫做坡比),用字母 表示;坡面与水平面的夹角叫做 ,记作α.
4.方位角:如图OA的方位角为 ;OC的方位角为
解直角三角形的应用题型主要有测量(测高求宽)问题,修路筑坝(坡度)问题和航海安全(方位角)问题等,解决问题的关键是构建直角三角形模型,把实际问题转化为数学问题来解决
例4:要测量学校一幢教学楼的高度.如图,先在点C测得教学楼AB的顶点A的仰角为30°,然后向教学楼前进60米到达点D,又测得点A的仰角为45°.请你根据这些数据,求出这幢教学楼的高度.(计算过程和结果均不取近似值)
方位角的应用
方位角是在规定“上北下南,左西右东”的原则下,确定物体的位置的一种方法;方位角往往与解直角三角形的知识联系在一起进行考查,当然有时也与行程问题中的方程联系在一起.
例5:如图,一艘轮船以每小时20海里的速度沿正北方向航行,在A处测得灯塔C在北偏西30°方向,轮船航行2小时后到达B处,在B处测得灯塔C在北偏西60°方向.当轮船到达灯塔C的正东方向的D处时,求此时轮船与灯塔C的距离.(结果保留根号)
中考题型:
1、如图所示,中原福塔(河南广播电视塔)是世界第—高钢塔.小明所在的课外活动小组在距地面268米高的室外观光层的点D处,测得地面上点B的俯角α为45°,点D到AO的距离DG为10米;从地面上的点B沿BO方向走50米到达点C处,测得塔尖A的仰角β为60°。请你根据以上数据计算塔高AO,并求出计算结果与实际塔高388米之间的误差.(参考数据:≈1.732,≈1.414.结果精确到0.1米)
(
30
°
48
°
)2、如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.
若坡角∠FAE=30°,求大树的高度.
(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,≈1.73)
(
E
C
D
B
A
、
68
°
60
°
)3、我国南水北调中线工程的起点是丹江口水库,按照工程计划,需对原水库大坝进行混凝土培厚加高,使坝高由原来的162米增加到176.6米,以抬高蓄水位.
如图是某一段坝体加高工程的截面示意图,其中原坝体的高为BE,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.
求工程完工后背水坡底端水平方向增加的宽度AC(结果精确到0.1米.
参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50,≈1.73).
4、在中俄“海上联合—2014”反潜演习中,我军舰A测得潜艇C的俯角为300.位于军舰A正上方1000米的反潜直升机B侧得潜艇C的俯角为680.试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数。参考数据:sin680≈0.9,cos680≈0.4,,tan680≈2.5.
≈1.7)
5、如图所示,A、B两地之间有一条河,原来从A地到B地需要经过DC,沿折线A→D→C→B到达,现在新建了桥EF,可直接沿直线AB从A地到达B地.已知BC=11km,∠A=45°,∠B=37°.桥DC和AB平行,则现在从A地到达B地可比原来少走多少路程?(结果精确到0.1km.参考数据:,sin37°≈0.60,cos37°≈0.80)
6、某宾馆为庆祝开业,在楼前悬挂了许多宣传条幅。如图所示,一条幅从楼顶A处放下,在楼前点C处拉直固定。小明为了测量此条幅的长度,他在E点测得楼顶的仰角为45°,在D点测得楼顶的仰角为31°且DE=16米。已知点C到大厦的距离BC=7米,∠ABD=90°.请根据以上数据求条幅的长度(结果保留整数。参考数据:tan31°≈0.60,sin31°≈0.52,cos31°≈0.86).
7、如图所示,电工李师傅借助梯子安装天花板上距地面2
.90m的顶灯.已知梯子由两个相同的矩形面组成,每个矩形面的长都被六条踏板七等分,使用时梯脚的固定跨度为1m.矩形面与地面所成的角α为78°.李师傅的身高为l.78m,当他攀升到头顶距天花板0.05~0.20m时,安装起来比较方便.他现在竖直站立在梯子的第三级踏板上,请你通过计算判断他安装是否比较方便?
(参考数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.70.)
年
级:
课时数:
第
次课
学员姓名:
辅导科目:
学科教师:
班主任:
授课日期及时段
年
月
日
时
分
——
时
分
授课主题
锐角三角函数
教学目标
(1)通过实例认识直角三角形的边角关系,即锐角三角函数(sinA,cosA,tanA),知道30°,45°,60°角的三角函数值.?
(2)会使用计算器由已知锐角求它的三角函数值,由已知三角函数值会求它的对应的锐角.?
(3)运用三角函数解决与直角三角形有关的简单的实际问题.?
(4)能综合运用直角三角形的勾股定理与边角关系解决简单的实际问题
重点难点
重点:解直角三角形及其应用?
难点:解直角三角形及其应用?
教学内容
一、导入
考向分析
结合近几年中考试题分析,锐角三角函数的内容考查主要有以下特点:
1.命题方式为锐角三角函数的定义、性质的应用、特殊角三角函数值的求法,
运用锐角三角函数解决与直角三角形有关的实际问题.
题型有选择题、填空题、解答题,多以中、低档题出现.
2.命题的热点为根据题中给出的信息构建图形,建立数学模型,
然后用解直角三角形的知识解决问题
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
二、知识梳理+经典例题
知识点一:锐角三角函数的概念与性质
1.锐角三角函数的概念:
在Rt△ABC中,∠C是直角,∠A、∠B、∠C的对边分别是a,b,c,如图.
(1)sinA=
=
(2)cosA=
=
(3)tanA=
=
锐角A的正弦、余弦、正切都叫做∠A的 .?
?特别提示:(1)当∠A为锐角时,0
(2)锐角A的正弦、正切值均随着角度的增大而增大,余弦值随着角度的增大而减小.
2.锐角三角函数的性质:
(1)若∠A为锐角,则有sin(90°-A)= ,
cos(90°-A)= ?
(2)同角三角函数的关系:
①平方关系:sin2A+cos2A=
②商数关系:
=
例1在Rt△ABC中,∠C=90°,AB=8,cosB=,则BC的长为( )
A.4 B.
C.
D.
知识巩固:(1)如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( )
A.
B.
C.
D.
(2)把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦函数值( )
A.不变
B.缩小为原来的
C.扩大为原来的3倍
D.不能确定
(3)△ABC中,a、b、c分别是∠A,∠B,∠C的对边,如果a2+b2=c2,那么下列结论正确的是( )
A.bcosB=c
B.csinA=a
C.atanA=b
D.tanB=
知识点二:特殊角的三角函数
???α? 30°?45°60°sinαcosαtanα
熟记特殊角的三角函数值是解决此类题的关键,特殊角的三角函数值可借助于直角三角板,根据三角函数定义得出:
例2:计算:sin30°+cos30°·tan60°
知识巩固:(1)计算(-2)2+tan45°-2cos60°
(2)(-2)2+
-2sin30°
知识点三:解直角三角形
1.直角三角形中,除直角外,一共有五个元素,即
和
.在直角三角形中,由已知元素求 元素的过程,就是解直角三角形.
2.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边.
在解直角三角形的过程中,常用的边角关系:
(1)三边之间的关系: ;?
(2)两锐角之间的关系: ;?
(3)边角之间的关系:sinA=
,sinB=
,cosA=
,
cosB=
,tanA=
,tanB=
解直角三角形的几种类型如下:
1.已知一条直角边和一个锐角(如a,∠A),其解法为:∠B=90°-∠A,c=
,b=
(或b=
);
2.已知斜边和一个锐角(如c,∠A),其解法为:∠B=90°-∠A,a=c·sinA,b=c·cosA(或b=
);
3.已知两直角边(如a,b),其解法为:c=,由tanA=
得∠A,∠B=90°-∠A;
4.已知斜边和一直角边(如c,a),其解法为:b=
,由sinA=,求出∠A,∠B=90°-∠A.
例3:如图,在△ABC中,∠B=45°,∠C=60°,AB=8,求AC.
知识巩固:(1)如图,小亮在太阳光线与地面成35°角时,测得树AB在地面上的影长BC=18
m,则树高AB约为
m(结果精确到0.1
m).
(2)为响应节能环保号召,小明家打算安装一台太阳能发电装置,已知当地安装电池板的最佳角度为54°.如图,按最佳角度安装,若斜杆AB长为1.50
m,则垂直于地面的竖杆AC长应为 m.
知识点四:解直角三角形的应用
1.解直角三角形的应用实际上是将实际问题通过图形使之转化到 中,用锐角三角函数、代数与几何知识综合求解.?
2.仰角和俯角:如图,在同一铅垂面内视线和水平线间的夹角,视线在水平线上方的叫做 ,在水平线下方的叫做 .?
3.坡度(坡比)、坡角:通常把坡面的 和 的比叫坡度(或叫做坡比),用字母 表示;坡面与水平面的夹角叫做 ,记作α.
4.方位角:如图OA的方位角为 ;OC的方位角为
解直角三角形的应用题型主要有测量(测高求宽)问题,修路筑坝(坡度)问题和航海安全(方位角)问题等,解决问题的关键是构建直角三角形模型,把实际问题转化为数学问题来解决
例4:要测量学校一幢教学楼的高度.如图,先在点C测得教学楼AB的顶点A的仰角为30°,然后向教学楼前进60米到达点D,又测得点A的仰角为45°.请你根据这些数据,求出这幢教学楼的高度.(计算过程和结果均不取近似值)
方位角的应用
方位角是在规定“上北下南,左西右东”的原则下,确定物体的位置的一种方法;方位角往往与解直角三角形的知识联系在一起进行考查,当然有时也与行程问题中的方程联系在一起.
例5:如图,一艘轮船以每小时20海里的速度沿正北方向航行,在A处测得灯塔C在北偏西30°方向,轮船航行2小时后到达B处,在B处测得灯塔C在北偏西60°方向.当轮船到达灯塔C的正东方向的D处时,求此时轮船与灯塔C的距离.(结果保留根号)
中考题型:
1、如图所示,中原福塔(河南广播电视塔)是世界第—高钢塔.小明所在的课外活动小组在距地面268米高的室外观光层的点D处,测得地面上点B的俯角α为45°,点D到AO的距离DG为10米;从地面上的点B沿BO方向走50米到达点C处,测得塔尖A的仰角β为60°。请你根据以上数据计算塔高AO,并求出计算结果与实际塔高388米之间的误差.(参考数据:≈1.732,≈1.414.结果精确到0.1米)
(
30
°
48
°
)2、如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.
若坡角∠FAE=30°,求大树的高度.
(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,≈1.73)
(
E
C
D
B
A
、
68
°
60
°
)3、我国南水北调中线工程的起点是丹江口水库,按照工程计划,需对原水库大坝进行混凝土培厚加高,使坝高由原来的162米增加到176.6米,以抬高蓄水位.
如图是某一段坝体加高工程的截面示意图,其中原坝体的高为BE,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.
求工程完工后背水坡底端水平方向增加的宽度AC(结果精确到0.1米.
参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50,≈1.73).
4、在中俄“海上联合—2014”反潜演习中,我军舰A测得潜艇C的俯角为300.位于军舰A正上方1000米的反潜直升机B侧得潜艇C的俯角为680.试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数。参考数据:sin680≈0.9,cos680≈0.4,,tan680≈2.5.
≈1.7)
5、如图所示,A、B两地之间有一条河,原来从A地到B地需要经过DC,沿折线A→D→C→B到达,现在新建了桥EF,可直接沿直线AB从A地到达B地.已知BC=11km,∠A=45°,∠B=37°.桥DC和AB平行,则现在从A地到达B地可比原来少走多少路程?(结果精确到0.1km.参考数据:,sin37°≈0.60,cos37°≈0.80)
6、某宾馆为庆祝开业,在楼前悬挂了许多宣传条幅。如图所示,一条幅从楼顶A处放下,在楼前点C处拉直固定。小明为了测量此条幅的长度,他在E点测得楼顶的仰角为45°,在D点测得楼顶的仰角为31°且DE=16米。已知点C到大厦的距离BC=7米,∠ABD=90°.请根据以上数据求条幅的长度(结果保留整数。参考数据:tan31°≈0.60,sin31°≈0.52,cos31°≈0.86).
7、如图所示,电工李师傅借助梯子安装天花板上距地面2
.90m的顶灯.已知梯子由两个相同的矩形面组成,每个矩形面的长都被六条踏板七等分,使用时梯脚的固定跨度为1m.矩形面与地面所成的角α为78°.李师傅的身高为l.78m,当他攀升到头顶距天花板0.05~0.20m时,安装起来比较方便.他现在竖直站立在梯子的第三级踏板上,请你通过计算判断他安装是否比较方便?
(参考数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.70.)
