北师大版九年级数学下册1.1锐角三角函数-同步测试(word版含答案)
文档属性
| 名称 | 北师大版九年级数学下册1.1锐角三角函数-同步测试(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 115.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览




文档简介
北师大版九年级数学下册第一章1.1锐角三角函数
同步测试
一.选择题
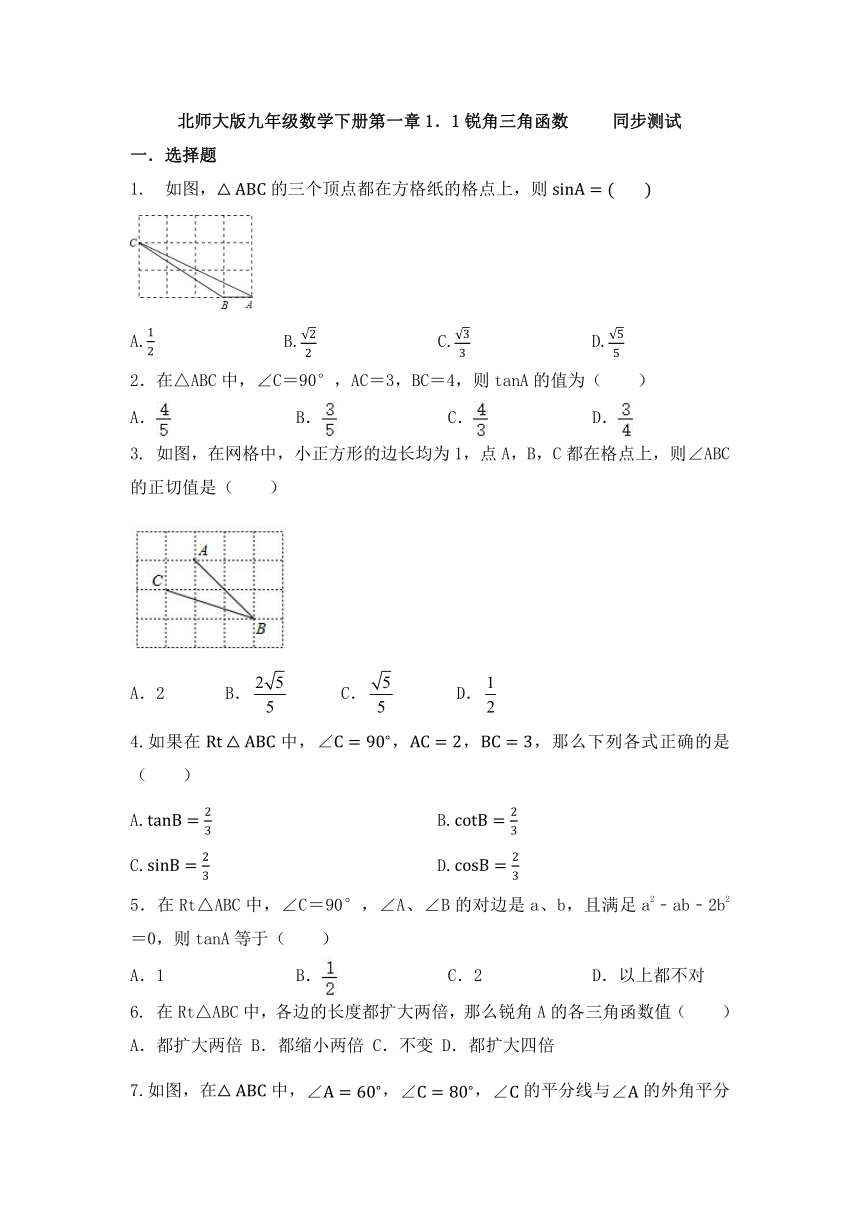
1.
如图,的三个顶点都在方格纸的格点上,则
A.
B.
C.
D.
2.在△ABC中,∠C=90°,AC=3,BC=4,则tanA的值为( )
A.
B.
C.
D.
3.
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
A.2
B.
C.
D.
4.如果在中,,,,那么下列各式正确的是(
)
A.
B.
C.
D.
5.在Rt△ABC中,∠C=90°,∠A、∠B的对边是a、b,且满足a2﹣ab﹣2b2=0,则tanA等于( )
A.1
B.
C.2
D.以上都不对
6.
在Rt△ABC中,各边的长度都扩大两倍,那么锐角A的各三角函数值( )
A.都扩大两倍
B.都缩小两倍
C.不变
D.都扩大四倍
7.如图,在中,,,的平分线与的外角平分线交于,连接,则的值是(
)
A.
B.
C.
D.
8.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则sinA的值为( )
A.
B.
C.
D.
9.
在Rt△ABC中,∠C=90°,AB=13,AC=12,则cosA=( )
A.
B.
C.
D.
10.在Rt△ABC中,各边都扩大5倍,则∠A的三角函数值( )
A.不变
B.扩大5倍
C.缩小5倍
D.不能确定
11.
如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
A.sinA的值越小,梯子越陡
B.cosA的值越小,梯子越陡
C.tanA的值越小,梯子越陡
D.陡缓程度与上A的函数值无关
12.sin58°、cos58°、cos28°的大小关系是( )
A.cos28°<cos58°<sin58°
B.sin58°<cos28°<cos58°
C.cos58°<sin58°<cos28°
D.sin58°<cos58°<cos28°
二.填空题
13.
如图,在Rt△ABC中,∠C=90°,AB=13,AC=7,则sinB=____________
14.在Rt△ABC中,∠C=90°,如果cosB=,BC=4,那么AB的长为 6 .
15.
比较下列三角函数值的大小:sin40°___________sin50°
16.在中,,如果,,那么________.
17.比较大小:sin40° = cos50°(填“>”、“<”或“=”)
18.如图,在Rt△ABC中,∠C=90°,BC=2,且tanA=,则AC=
.
19.比较大小:
(1)cos35°
cos45°,tan50°
tan60°;
(2)若sinα=0.3276,sinβ=0.3274,则α
β.
20.如图,直角三角形纸片的两直角边长分别为,,现将如图那样折叠,使点与点重合,折痕为,则的值是________.
三.解答题
21.
如图,在Rt△ABC中,∠C=90°,AB=2BC,求sinB的值
22.
在中,,若,写出的四个三角函数的值.
23.
在Rt△ABC中,∠C=90°,如果AC:BC=3:4,求cosA的值
24..如图,在Rt△ABC中,∠C=90°,tanA=,BC=2,求AB的长.
25.
在中,,、、分别是、、的对边.请利用三角函数的定义探讨能否用边的式子表示?请写出你必要的理由.
?
26.在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c.若a=2,sin,求b和c.
27.如图,在中,,是直角边上一点,于点,,,求的值.
?
28.(1)如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值的变化规律;
(2)根据你探索到的规律,试比较18°,34°,52°,65°,88°,这些角的正弦值的大小和余弦值的大小;
(3)比较大小:(在空格处填写“<”或“>”或“=”)
若∠α=45°,则sinα
cosα;若∠α<45°,则sinα
cosα;若∠α>45°,则sinα
cosα;
(4)利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小:
sin10°,cos30°,sin50°,cos70°.
答案提示
1.
D.2.C.3.D.4.
A.5.C.6.C.7.
D.8.A.9.C.10.A.11.B.12.C.
.
14.6.
15.<.
16.
.
17.=.
18.6.
19.(1)>,<;(2)>.
20.
21.
解:
∵AB=2BC,
∴AC=
∴sinB=
故答案为
22.
解:,,
由勾股定理,得
,
,
,
.
23.解:如图所示:∵在Rt△ABC中,∠C=90°,AC:BC=3:4,
∴设AC=3x,BC=4x,故AB=5x,
则cosA=
故答案为:
24.解:∵在Rt△ABC中,∠C=90°,
∴tanA==.
∵BC=2,
∴=,AC=6.
∵AB2=AC2+BC2=40,
∴AB=.
25.
解:∵,,
∴,
即.
26.解:如图,
∵a=2,sin,
∴c===6,
则b===4.
27.
解:∵,,
∴,
又∵,
∴,
∴,
设,,
由勾股定理得:,
在中,.
28.解:(1)在图(1)中,令AB1=AB2=AB3,B1C1⊥AC于点C1,B2C2⊥AC于点C2,B3C3⊥AC于点C3,
显然有:B1C1>B2C2>B3C3,∠B1AC>∠B2AC>∠B3AC.
∵sin∠B1AC=,sin∠B2AC=,sin∠B3AC=,
而>>.
∴sin∠B1AC>sin∠B2AC>sin∠B3AC.
在图(2)中,Rt△ACB3中,∠C=90°,
cos∠B1AC=,cos∠B2AC=,cos∠B3AC=,
∵AB3<AB2<AB1,
∴>>.
即cos∠B3AC>cos∠B2AC>cos∠B1AC.
(2)sin88°>sin65°>sin52°>sin34°>sin18°;
cos88°<cos65°<cos52°<cos34°<cos18°.
(3)若∠α=45°,则sinα=cosα;若∠α<45°,则sinα<cosα;若∠α>45°,则sinα>cosα.
(4)cos30°>sin50°>cos70°>sin10°.
同步测试
一.选择题
1.
如图,的三个顶点都在方格纸的格点上,则
A.
B.
C.
D.
2.在△ABC中,∠C=90°,AC=3,BC=4,则tanA的值为( )
A.
B.
C.
D.
3.
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
A.2
B.
C.
D.
4.如果在中,,,,那么下列各式正确的是(
)
A.
B.
C.
D.
5.在Rt△ABC中,∠C=90°,∠A、∠B的对边是a、b,且满足a2﹣ab﹣2b2=0,则tanA等于( )
A.1
B.
C.2
D.以上都不对
6.
在Rt△ABC中,各边的长度都扩大两倍,那么锐角A的各三角函数值( )
A.都扩大两倍
B.都缩小两倍
C.不变
D.都扩大四倍
7.如图,在中,,,的平分线与的外角平分线交于,连接,则的值是(
)
A.
B.
C.
D.
8.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则sinA的值为( )
A.
B.
C.
D.
9.
在Rt△ABC中,∠C=90°,AB=13,AC=12,则cosA=( )
A.
B.
C.
D.
10.在Rt△ABC中,各边都扩大5倍,则∠A的三角函数值( )
A.不变
B.扩大5倍
C.缩小5倍
D.不能确定
11.
如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
A.sinA的值越小,梯子越陡
B.cosA的值越小,梯子越陡
C.tanA的值越小,梯子越陡
D.陡缓程度与上A的函数值无关
12.sin58°、cos58°、cos28°的大小关系是( )
A.cos28°<cos58°<sin58°
B.sin58°<cos28°<cos58°
C.cos58°<sin58°<cos28°
D.sin58°<cos58°<cos28°
二.填空题
13.
如图,在Rt△ABC中,∠C=90°,AB=13,AC=7,则sinB=____________
14.在Rt△ABC中,∠C=90°,如果cosB=,BC=4,那么AB的长为 6 .
15.
比较下列三角函数值的大小:sin40°___________sin50°
16.在中,,如果,,那么________.
17.比较大小:sin40° = cos50°(填“>”、“<”或“=”)
18.如图,在Rt△ABC中,∠C=90°,BC=2,且tanA=,则AC=
.
19.比较大小:
(1)cos35°
cos45°,tan50°
tan60°;
(2)若sinα=0.3276,sinβ=0.3274,则α
β.
20.如图,直角三角形纸片的两直角边长分别为,,现将如图那样折叠,使点与点重合,折痕为,则的值是________.
三.解答题
21.
如图,在Rt△ABC中,∠C=90°,AB=2BC,求sinB的值
22.
在中,,若,写出的四个三角函数的值.
23.
在Rt△ABC中,∠C=90°,如果AC:BC=3:4,求cosA的值
24..如图,在Rt△ABC中,∠C=90°,tanA=,BC=2,求AB的长.
25.
在中,,、、分别是、、的对边.请利用三角函数的定义探讨能否用边的式子表示?请写出你必要的理由.
?
26.在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c.若a=2,sin,求b和c.
27.如图,在中,,是直角边上一点,于点,,,求的值.
?
28.(1)如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值的变化规律;
(2)根据你探索到的规律,试比较18°,34°,52°,65°,88°,这些角的正弦值的大小和余弦值的大小;
(3)比较大小:(在空格处填写“<”或“>”或“=”)
若∠α=45°,则sinα
cosα;若∠α<45°,则sinα
cosα;若∠α>45°,则sinα
cosα;
(4)利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小:
sin10°,cos30°,sin50°,cos70°.
答案提示
1.
D.2.C.3.D.4.
A.5.C.6.C.7.
D.8.A.9.C.10.A.11.B.12.C.
.
14.6.
15.<.
16.
.
17.=.
18.6.
19.(1)>,<;(2)>.
20.
21.
解:
∵AB=2BC,
∴AC=
∴sinB=
故答案为
22.
解:,,
由勾股定理,得
,
,
,
.
23.解:如图所示:∵在Rt△ABC中,∠C=90°,AC:BC=3:4,
∴设AC=3x,BC=4x,故AB=5x,
则cosA=
故答案为:
24.解:∵在Rt△ABC中,∠C=90°,
∴tanA==.
∵BC=2,
∴=,AC=6.
∵AB2=AC2+BC2=40,
∴AB=.
25.
解:∵,,
∴,
即.
26.解:如图,
∵a=2,sin,
∴c===6,
则b===4.
27.
解:∵,,
∴,
又∵,
∴,
∴,
设,,
由勾股定理得:,
在中,.
28.解:(1)在图(1)中,令AB1=AB2=AB3,B1C1⊥AC于点C1,B2C2⊥AC于点C2,B3C3⊥AC于点C3,
显然有:B1C1>B2C2>B3C3,∠B1AC>∠B2AC>∠B3AC.
∵sin∠B1AC=,sin∠B2AC=,sin∠B3AC=,
而>>.
∴sin∠B1AC>sin∠B2AC>sin∠B3AC.
在图(2)中,Rt△ACB3中,∠C=90°,
cos∠B1AC=,cos∠B2AC=,cos∠B3AC=,
∵AB3<AB2<AB1,
∴>>.
即cos∠B3AC>cos∠B2AC>cos∠B1AC.
(2)sin88°>sin65°>sin52°>sin34°>sin18°;
cos88°<cos65°<cos52°<cos34°<cos18°.
(3)若∠α=45°,则sinα=cosα;若∠α<45°,则sinα<cosα;若∠α>45°,则sinα>cosα.
(4)cos30°>sin50°>cos70°>sin10°.
