北师大版九年级数学下册 第3章 圆压轴题型 提升训练(五)(word解析版)
文档属性
| 名称 | 北师大版九年级数学下册 第3章 圆压轴题型 提升训练(五)(word解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 312.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览

文档简介
九年级数学下册
第3章
《圆》
压轴题型提升训练(五)
1.已知:AB是⊙O的弦,CD是⊙O的直径,AB与CD相交于点E,连接AC、BC,AC=BC.
(1)如图1,求证:AB⊥CD;
(2)如图2,过点E作EF∥BC,交BO的延长线于点F,连接CF,求证:AE=CF;
(3)如图3,在(2)的条件下,DE>OE,点G在OB的延长线上,连接DG,∠DGF=∠CEF,DG=20,FG=23,求AB的长.
2.如图,点D是等边三角形ABC外接圆的上一点(与点A,C不重合),CE∥AD交BD于点E.
(1)求证:△CDE是等边三角形;
(2)求证:AD=BE;
(3)如果AD=2,CD=4,求AC的长.
3.如图,已知⊙O是△ABC的外接圆,直径AD与BC垂直,垂足为点E.
(1)求证:∠ABC=∠ACB;
(2)连接OB,CD,若OB=,CD=5,求CE的长.
4.△ABE内接于⊙O,C在劣弧AB上,连CO交AB于D,连BO,∠COB=∠E.
(1)如图1,求证:CO⊥AB;
(2)如图2,BO平分∠ABE,求证:AB=BE;
(3)如图3,在(2)条件下,点P在OC延长线上,连PB,ET⊥AB于T,∠P=2∠AET,ET=18,OP=25,求⊙O半径的长.
5.如图,四边形ABCD内接于⊙O,连接AC、BD相交于点E.
(1)如图1,若AC=BD,求证:AE=DE;
(2)如图2,若AC⊥BD,连接OC,求证:∠OCD=∠ACB.
6.如图,在△ABC中,AB=AC,点D在BC边上,且AD=BD,⊙O是△ACD的外接圆,AE是⊙O的直径.
(1)求证:AB是⊙O的切线;
(2)若AB=2,AD=3,求直径AE的长.
7.在平面直角坐标系xOy中,给出如下定义:若点P在图形M上,点Q在图形N上,称线段PQ长度的最小值为图形M,N的密距,记为d(M,N),特别地,若图形M,N有公共点,规定d(M,N)=0.
(1)如图1,⊙O的半径为3,
①点A(0,1),B(4,3),则d(A,⊙O)=
,d(B,⊙O)=
.
②已知直线l:y=x+b与⊙O的密距d(1,⊙O)=,求b的值.
(2)如图2,C为x轴正半轴上的一点,⊙C的半径为1,直线y=x与x轴交于点D,与y轴交于点E,其中∠ODE=30°,线段DE与⊙C的密距d(DE,⊙O)<.请直接写出圆心C的横坐标m的取值范围.
8.如图,E点为x轴正半轴上一点,⊙E交x轴于A、B两点,交y轴于C、D两点,P点为劣弧上一个动点,连接PA,PC,且A(﹣1,0),E(1,0).
(1)如图1,求点C的坐标和∠P的度数;
(2)如图2,若CQ平分∠PCD交PA于Q点,当P点在运动时,线段AQ的长度是否发生变化;若不变,求出其值,若发生变化,求出变化的范围;
(3)如图3,连接PD,当P点在运动时(不与B、C两点重合),求的值.
9.已知:△ABC内接于⊙O,∠BAC的角平分线AD交⊙O于点D.
(1)如图①,以点D为圆心,DB长为半径作弧,交AD于点I.求证:点I是△ABC的内心;
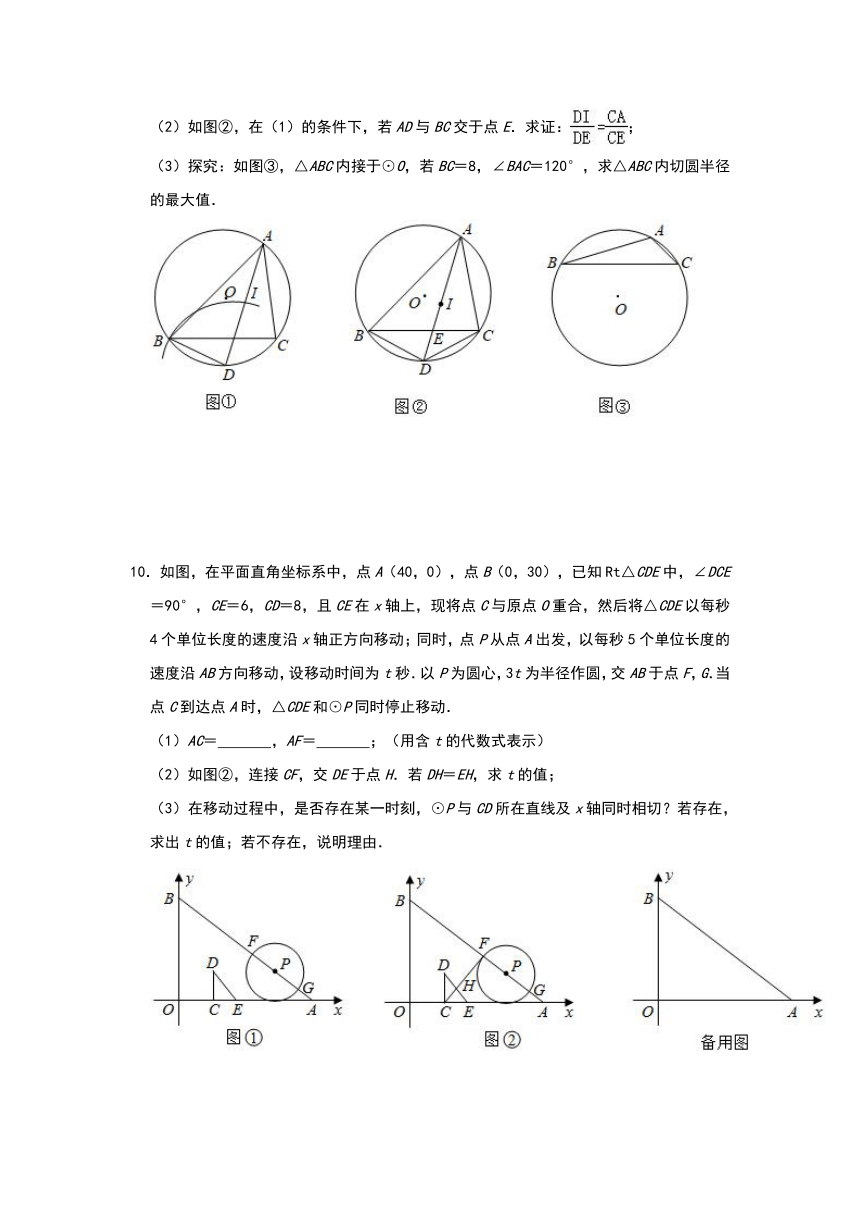
(2)如图②,在(1)的条件下,若AD与BC交于点E.求证:;
(3)探究:如图③,△ABC内接于⊙O,若BC=8,∠BAC=120°,求△ABC内切圆半径的最大值.
10.如图,在平面直角坐标系中,点A(40,0),点B(0,30),已知Rt△CDE中,∠DCE=90°,CE=6,CD=8,且CE在x轴上,现将点C与原点O重合,然后将△CDE以每秒4个单位长度的速度沿x轴正方向移动;同时,点P从点A出发,以每秒5个单位长度的速度沿AB方向移动,设移动时间为t秒.以P为圆心,3t为半径作圆,交AB于点F,G.当点C到达点A时,△CDE和⊙P同时停止移动.
(1)AC=
,AF=
;(用含t的代数式表示)
(2)如图②,连接CF,交DE于点H.若DH=EH,求t的值;
(3)在移动过程中,是否存在某一时刻,⊙P与CD所在直线及x轴同时相切?若存在,求出t的值;若不存在,说明理由.
参考答案
1.解:(1)如图1,∵AC=BC,AO=BO,CO=CO,
∴△AOC≌△BOC(SSS),
∴∠ACO=∠BCO,
∴CE⊥AB,
即AB⊥CD;
(2)如图2,∵CO=OB,
∴∠OCB=∠OBC,
∵EF∥BC,
∴∠OEF=∠OBC,∠OEF=∠OCB,
∴∠OFE=∠OEF,
∴OE=OF,
∴BF=BO+OF=CO+OE=CE,
而BC=BC,∠CBF=∠BCE,
∴△CEB≌△CFB(SAS),
∴∠CEB=∠CFB=90°,EB=FB,
而AE=BE,
∴AE=CF;
(3)过点D作DM⊥FG于点M,
∵∠OMD=∠CFB=90°,∠COF=∠MOD,OC=OD,
∴△CFO≌△DMO(AAS),
∴DM=CF,
又∠G=∠EFB=∠FBC=∠BCE,∠DMG=∠CFB=90°,
∴△FCB≌△MDG(AAS),
∴BC=DG=20,GM=BF,
∴FM=BG,则FO=BG,
设FO=x,则BG=2x,则BF=23﹣2x,CO=BO=23﹣3x,
∵CF2=BC2﹣BF2=202﹣(23﹣2x)2,CF2=CO2﹣FO2=(23﹣3x)2﹣x2,
即202﹣(23﹣2x)2=(23﹣3x)2﹣x2,解得x=(舍去)或,
∴CF==12,
则AB=2AE=2CF=24.
42.(1)证明:∵△ABC为等边三角形,
∴∠BAC=∠ACB=60°,
∴∠BDC=∠BAC=60°,∠ADB=∠ACB=60°,
∵CE∥AD,
∴∠DEC=∠ADB=60°,
∴∠DCE=∠DEC=∠BDC=60°,
∴△CDE为等边三角形;
(2)证明:∵△ABC和△CDE为等边三角形,
∴BC=AC,CE=CD,
∵∠BCE+∠ACE=∠ACD+∠ACE=60°,
∴∠BCE=∠ACD,
在△BCE和△ACB中,
,
∴△BCE≌△ACD(SAS),
∴BE=AD;
(3)解:过点C作CF⊥AD于F,
∵∠CDF=∠ABC=60°,
∴∠DCF=30°,
∴DF=CD=2,
∴AF=4,
∴CF2=CD2﹣DF2=42﹣22=12,
∴AC=.
43.(1)证明:∵AD⊥BC,
∴=,
∴∠ABC=∠ACB;
(2)解:连接OC,如图,
设OE=x,则DE=OD﹣OE=﹣﹣x,
在Rt△OEC中,CE2=OC2﹣OE2=()2﹣x2,
在Rt△CDE中,CE2=CD2﹣DE2=52﹣(﹣x)2,
∴()2﹣x2=52﹣(﹣x)2,解得x=,
∴CE==.
44.(1)证明:如图1中,连接AO.
∵∠AOB=2∠E,∠COB=∠E,
∴∠AOC=∠BOC,
∵OA=OB,
∴OC⊥AB.
(2)证明:如图2中,连接OA,OE.
∵OA=OB=OE,
∴∠OAB=∠OBA,∠OEB=∠OBE,
∵OB平分∠ABE,
∴∠ABO=∠EBO,
∴∠OAB=∠OEB,
∴△ABO≌△EBO(AAS),
∴AB=EB.
(3)解:如图3中,过点A作AK⊥PB于K,AH⊥BE于H.
∵OC⊥AB,
∴=,
∴∠AEB=∠BOD,
∵AB=BE,
∴∠BAE=∠AEB,
∵ET⊥AB,
∴∠ATE=∠BDO=90°,
∴∠EAT+∠AET=90°,∠BOD+∠OBD=90°,
∴∠AET=∠OBD=∠OBE,
∵∠BPC=2∠AET,∠ABE=2∠OBE,
∴∠BPO=∠ABE,
∵∠PBD+∠BPD=90°,
∴∠PBD+∠ABE=90°,
∴∠PBE=90°,
∵AK⊥BP,AH⊥BE,
∴∠AKB=∠AHB=∠KBE=90°,
∴四边形AKBH是矩形,
∴AH=BK,
∵∠BOP+∠ABO=90°,∠PBO+∠EBO=90°,∠ABO=∠EBO,
∴∠POB=∠PBO,
∴PO=PB=25,
∵BA=BE,ET⊥AB,AH⊥BE,
∴AH=ET=18,
∴BK=AH=18,
∵PB=25,
∴PK=PB﹣BK=7,
∵OP垂直平分线段AB,
∴PA=PB=25,
∵∠AKP=90°,
∴AK===24,
∴AB===30,
∴AD=BD=15,
∴PD===20,
∴OD=OP﹣PD=25﹣20=5,
∴OB===5.
∴⊙O的半径为5.
45.证明:(1)∵AC=BD,
∴=,
即+=+,
∴=,
∴∠ADB=∠CAD,
∴AE=DE;
(2)作直径CF,连接DF,如图2,
∵AC⊥BD,
∴∠AED=90°,
∴∠ADE+∠CAD=90°,
∵∠ACB=∠ADE,∠F=∠CAD,
∴∠ACB+∠F=90°,
∵CF为直径,
∴∠CDF=90°,
∴∠F+∠FCD=90°,
∴∠ACB=∠FCD,
即∠OCD=∠ACB.
46.(1)证明:连接DE,如图1,
∵AB=AC,AD=BD,
∴∠B=∠BAD,∠B=∠C,
∴∠C=∠E,
∴∠E=∠BAD,
∵AE是⊙O的直径,
∴∠ADE=90°,
∴∠E+∠DAE=90°,
∴∠BAD+∠DAE=90°,
即∠BAE=90°,
∴AE⊥AB,
∴直线AB是⊙O的切线;
(2)解:如图2,作AH⊥BC,垂足为点H,
∵AB=AC,
∴BH=CH,
∵∠B=∠C=∠BAD,
∴△ABC∽△DBA,
∴,
即AB2=BD?BC,
又AB=2,BD=AD=3,
∴BC=8,
在Rt△ABH中,BH=CH=4,
∴AH===2,
∵∠E=∠B,∠ADE=∠AHB,
∴△AED∽△ABH,
∴,
∴=3.
47.解:(1)①连接OB,过点B作BT⊥x轴于T,如图1①,
∵⊙O的半径为2,点A(0,1),
∴d(A,⊙O)=2﹣1=1.
∵B(4,3),
∴OB==5,
∴d(B,⊙O)=5﹣2=3.
故答案为:1,3;
②设直线l:y=x+b与x轴、y轴分别交于点P、Q,过点O作OH⊥PQ于H,设OH与⊙O交于点G,如图1②,
∴P(﹣b,0),Q(0,b),
∴OP=|b|,OQ=|b|,
∴PQ=|b|.
∵S△OPQ=OP?OQ=PQ?OH,
∴OH==|b|.
∵直线l:y=x+b与⊙O的密距d(l,⊙O)=,
∴|b|=2+=,
∴b=±4;
(2)过点C作CN⊥DE于N,如图2.
∵点D、E分别是直线y=﹣x+与x轴、y轴的交点,
∴D(4,0),E(0,),
∴OD=4,OE=,
∴tan∠ODE==,
∴∠ODE=30°.
①当点C在点D左边时,m<4.
∵OC=m,
∴CD=4﹣m,
∴CN=CD?sin∠CDN=(4﹣m)=2﹣m.
∵线段DE与⊙C的密距d(DE,⊙C)<,
∴0<2﹣m<+1,
∴1<m<4;
②当点C与点D重合时,m=4.
此时d(DE,⊙C)=0.
③当点C在点D的右边时,m>4.
∵线段DE与⊙C的密距d(DE,⊙C)<,
∴CD﹣1<,
∴(m﹣4)<+1,
∴m<,
∴4<m<.
综上所述:1<m<.
48.解:(1)如图1,连接EC,AC.
∵A(﹣1,0),E(1,0),
∴OA=OE=1,
∴AE=CE=2
∵OE=1,
∴OC===,
∴C(0,),
∵CO⊥AE,OA=OE,
∴CA=CE,
∴CA=CE=AE,
∴△ACE是等边三角形,
∴∠AEC=60°,
∴∠P=∠AEC=30°.
(2)不发生变化.
如图2,连接CB,则∠CPA=∠CBA=∠ACO,
∵∠ACQ=∠ACO+∠OCQ,∠AQC=∠CPA+∠PCQ,
∵CQ平分∠PCD,
∴∠PCQ=∠OCQ,
∴∠ACQ=∠AQC,得AQ=AC=2;
(3)结论①不变,在PD的延长线上截取DM=PC,则PC+PD=PM,
如图3,连接AM,
在△PAC和△MAD中,
,
∴△PAC≌△MAD(SAS),
∴MA=PA,∠MAP=∠DAC=120°,
∴△PAM是以30°为底角的等腰三角形,
过点A作AK⊥PM于K,则MK=PK=AM?cos30°=AM,
∴PM=PA,
∴==.
49.(1)证明:如图①中,连接BI.
∵DB=DI,
∴∠DBI=∠DIB,
∵∠DIB=∠IAB+∠IBA,∠DBI=∠IBC+∠DBC,
又∵∠DBC=∠DAC=∠DAB,
∴∠DBC=∠IAB,
∴∠IBA=∠IBC,即BI平分∠ABC,
∴点I是△ABC的内心.
(2)证明:如图②中,
∵∠BDA=∠BCA,∠DBC=∠DAC,
∴△BDE∽△ACE,
∴=,
∵DB=DI,
∴=.
(3)解:如图③中,作∠BAC的角平分线AD交⊙O于D,连接BD,DC,以D为圆心,DB为半径作作弧,交AD于点I,
由(1)点I是△ABC的内心.
∵IH⊥AC,
∴IH是△ABC的内切圆的半径,
在△AIH中,∠IAH=∠BAC=60°,
∴IH=AI,故欲求IH的最大值只要求出AI的最大值,
∵∠DBC=∠DAC=60°,∠DCB=∠DAB=60°,
∴△BDC是等边三角形,
∴DB=CB=8,即DI=8,
作直径DF,
在Rt△BDF中,∠DFB=60°,DB=8,
∴DF=,即直径为,
∴AI的最大值为﹣8,
∴△ABC的内切圆的半径的最大值为8﹣4.
50.解:(1)∵点A(40,0),点B(0,30),
∴OA=40,OB=30,
∴AC=AO﹣OC=40﹣4t,AF=AP+PF=5t+3t=8t.
故答案为:40﹣4t,8t.
(2)∵CE=6,CD=8,OA=30,OB=40,
∴==,
∵∠DCE=∠AOB=∠DCE=90°,
∴△DCE∽△AOB,
∴∠D=∠BAO,
在Rt△CDE中,DH=ED,
∴CH=DH=EH,
∴∠HCE=∠HEC,
∴∠HCE+∠BAO=∠HEC+∠D=90°,
∴∠AFC=90°,
∵∠AFC=∠AOB=90°,∠FAC=∠OAB,
∴△AF∽△AOB,
∴=,
∴=,
∴t=.
(3)过点P作PM⊥OA于M,则PA=5t,PM=3t,AM=4t,
∴⊙P与x轴相切,
①如图③﹣1中,当⊙P在直线CD的右侧时,设直线CD与⊙P相切于点N,连接PN,则四边形PMCN是正方形.
∴CM=PM,
∴40﹣4t﹣4t=3t,
∴t=.
②如图③﹣2中,当⊙P在直线CD的左侧时,则有40﹣4t=4t﹣3t,解得t=8.
综上所述,当t=或8时,⊙P与CD所在直线及x轴同时相切.
第3章
《圆》
压轴题型提升训练(五)
1.已知:AB是⊙O的弦,CD是⊙O的直径,AB与CD相交于点E,连接AC、BC,AC=BC.
(1)如图1,求证:AB⊥CD;
(2)如图2,过点E作EF∥BC,交BO的延长线于点F,连接CF,求证:AE=CF;
(3)如图3,在(2)的条件下,DE>OE,点G在OB的延长线上,连接DG,∠DGF=∠CEF,DG=20,FG=23,求AB的长.
2.如图,点D是等边三角形ABC外接圆的上一点(与点A,C不重合),CE∥AD交BD于点E.
(1)求证:△CDE是等边三角形;
(2)求证:AD=BE;
(3)如果AD=2,CD=4,求AC的长.
3.如图,已知⊙O是△ABC的外接圆,直径AD与BC垂直,垂足为点E.
(1)求证:∠ABC=∠ACB;
(2)连接OB,CD,若OB=,CD=5,求CE的长.
4.△ABE内接于⊙O,C在劣弧AB上,连CO交AB于D,连BO,∠COB=∠E.
(1)如图1,求证:CO⊥AB;
(2)如图2,BO平分∠ABE,求证:AB=BE;
(3)如图3,在(2)条件下,点P在OC延长线上,连PB,ET⊥AB于T,∠P=2∠AET,ET=18,OP=25,求⊙O半径的长.
5.如图,四边形ABCD内接于⊙O,连接AC、BD相交于点E.
(1)如图1,若AC=BD,求证:AE=DE;
(2)如图2,若AC⊥BD,连接OC,求证:∠OCD=∠ACB.
6.如图,在△ABC中,AB=AC,点D在BC边上,且AD=BD,⊙O是△ACD的外接圆,AE是⊙O的直径.
(1)求证:AB是⊙O的切线;
(2)若AB=2,AD=3,求直径AE的长.
7.在平面直角坐标系xOy中,给出如下定义:若点P在图形M上,点Q在图形N上,称线段PQ长度的最小值为图形M,N的密距,记为d(M,N),特别地,若图形M,N有公共点,规定d(M,N)=0.
(1)如图1,⊙O的半径为3,
①点A(0,1),B(4,3),则d(A,⊙O)=
,d(B,⊙O)=
.
②已知直线l:y=x+b与⊙O的密距d(1,⊙O)=,求b的值.
(2)如图2,C为x轴正半轴上的一点,⊙C的半径为1,直线y=x与x轴交于点D,与y轴交于点E,其中∠ODE=30°,线段DE与⊙C的密距d(DE,⊙O)<.请直接写出圆心C的横坐标m的取值范围.
8.如图,E点为x轴正半轴上一点,⊙E交x轴于A、B两点,交y轴于C、D两点,P点为劣弧上一个动点,连接PA,PC,且A(﹣1,0),E(1,0).
(1)如图1,求点C的坐标和∠P的度数;
(2)如图2,若CQ平分∠PCD交PA于Q点,当P点在运动时,线段AQ的长度是否发生变化;若不变,求出其值,若发生变化,求出变化的范围;
(3)如图3,连接PD,当P点在运动时(不与B、C两点重合),求的值.
9.已知:△ABC内接于⊙O,∠BAC的角平分线AD交⊙O于点D.
(1)如图①,以点D为圆心,DB长为半径作弧,交AD于点I.求证:点I是△ABC的内心;
(2)如图②,在(1)的条件下,若AD与BC交于点E.求证:;
(3)探究:如图③,△ABC内接于⊙O,若BC=8,∠BAC=120°,求△ABC内切圆半径的最大值.
10.如图,在平面直角坐标系中,点A(40,0),点B(0,30),已知Rt△CDE中,∠DCE=90°,CE=6,CD=8,且CE在x轴上,现将点C与原点O重合,然后将△CDE以每秒4个单位长度的速度沿x轴正方向移动;同时,点P从点A出发,以每秒5个单位长度的速度沿AB方向移动,设移动时间为t秒.以P为圆心,3t为半径作圆,交AB于点F,G.当点C到达点A时,△CDE和⊙P同时停止移动.
(1)AC=
,AF=
;(用含t的代数式表示)
(2)如图②,连接CF,交DE于点H.若DH=EH,求t的值;
(3)在移动过程中,是否存在某一时刻,⊙P与CD所在直线及x轴同时相切?若存在,求出t的值;若不存在,说明理由.
参考答案
1.解:(1)如图1,∵AC=BC,AO=BO,CO=CO,
∴△AOC≌△BOC(SSS),
∴∠ACO=∠BCO,
∴CE⊥AB,
即AB⊥CD;
(2)如图2,∵CO=OB,
∴∠OCB=∠OBC,
∵EF∥BC,
∴∠OEF=∠OBC,∠OEF=∠OCB,
∴∠OFE=∠OEF,
∴OE=OF,
∴BF=BO+OF=CO+OE=CE,
而BC=BC,∠CBF=∠BCE,
∴△CEB≌△CFB(SAS),
∴∠CEB=∠CFB=90°,EB=FB,
而AE=BE,
∴AE=CF;
(3)过点D作DM⊥FG于点M,
∵∠OMD=∠CFB=90°,∠COF=∠MOD,OC=OD,
∴△CFO≌△DMO(AAS),
∴DM=CF,
又∠G=∠EFB=∠FBC=∠BCE,∠DMG=∠CFB=90°,
∴△FCB≌△MDG(AAS),
∴BC=DG=20,GM=BF,
∴FM=BG,则FO=BG,
设FO=x,则BG=2x,则BF=23﹣2x,CO=BO=23﹣3x,
∵CF2=BC2﹣BF2=202﹣(23﹣2x)2,CF2=CO2﹣FO2=(23﹣3x)2﹣x2,
即202﹣(23﹣2x)2=(23﹣3x)2﹣x2,解得x=(舍去)或,
∴CF==12,
则AB=2AE=2CF=24.
42.(1)证明:∵△ABC为等边三角形,
∴∠BAC=∠ACB=60°,
∴∠BDC=∠BAC=60°,∠ADB=∠ACB=60°,
∵CE∥AD,
∴∠DEC=∠ADB=60°,
∴∠DCE=∠DEC=∠BDC=60°,
∴△CDE为等边三角形;
(2)证明:∵△ABC和△CDE为等边三角形,
∴BC=AC,CE=CD,
∵∠BCE+∠ACE=∠ACD+∠ACE=60°,
∴∠BCE=∠ACD,
在△BCE和△ACB中,
,
∴△BCE≌△ACD(SAS),
∴BE=AD;
(3)解:过点C作CF⊥AD于F,
∵∠CDF=∠ABC=60°,
∴∠DCF=30°,
∴DF=CD=2,
∴AF=4,
∴CF2=CD2﹣DF2=42﹣22=12,
∴AC=.
43.(1)证明:∵AD⊥BC,
∴=,
∴∠ABC=∠ACB;
(2)解:连接OC,如图,
设OE=x,则DE=OD﹣OE=﹣﹣x,
在Rt△OEC中,CE2=OC2﹣OE2=()2﹣x2,
在Rt△CDE中,CE2=CD2﹣DE2=52﹣(﹣x)2,
∴()2﹣x2=52﹣(﹣x)2,解得x=,
∴CE==.
44.(1)证明:如图1中,连接AO.
∵∠AOB=2∠E,∠COB=∠E,
∴∠AOC=∠BOC,
∵OA=OB,
∴OC⊥AB.
(2)证明:如图2中,连接OA,OE.
∵OA=OB=OE,
∴∠OAB=∠OBA,∠OEB=∠OBE,
∵OB平分∠ABE,
∴∠ABO=∠EBO,
∴∠OAB=∠OEB,
∴△ABO≌△EBO(AAS),
∴AB=EB.
(3)解:如图3中,过点A作AK⊥PB于K,AH⊥BE于H.
∵OC⊥AB,
∴=,
∴∠AEB=∠BOD,
∵AB=BE,
∴∠BAE=∠AEB,
∵ET⊥AB,
∴∠ATE=∠BDO=90°,
∴∠EAT+∠AET=90°,∠BOD+∠OBD=90°,
∴∠AET=∠OBD=∠OBE,
∵∠BPC=2∠AET,∠ABE=2∠OBE,
∴∠BPO=∠ABE,
∵∠PBD+∠BPD=90°,
∴∠PBD+∠ABE=90°,
∴∠PBE=90°,
∵AK⊥BP,AH⊥BE,
∴∠AKB=∠AHB=∠KBE=90°,
∴四边形AKBH是矩形,
∴AH=BK,
∵∠BOP+∠ABO=90°,∠PBO+∠EBO=90°,∠ABO=∠EBO,
∴∠POB=∠PBO,
∴PO=PB=25,
∵BA=BE,ET⊥AB,AH⊥BE,
∴AH=ET=18,
∴BK=AH=18,
∵PB=25,
∴PK=PB﹣BK=7,
∵OP垂直平分线段AB,
∴PA=PB=25,
∵∠AKP=90°,
∴AK===24,
∴AB===30,
∴AD=BD=15,
∴PD===20,
∴OD=OP﹣PD=25﹣20=5,
∴OB===5.
∴⊙O的半径为5.
45.证明:(1)∵AC=BD,
∴=,
即+=+,
∴=,
∴∠ADB=∠CAD,
∴AE=DE;
(2)作直径CF,连接DF,如图2,
∵AC⊥BD,
∴∠AED=90°,
∴∠ADE+∠CAD=90°,
∵∠ACB=∠ADE,∠F=∠CAD,
∴∠ACB+∠F=90°,
∵CF为直径,
∴∠CDF=90°,
∴∠F+∠FCD=90°,
∴∠ACB=∠FCD,
即∠OCD=∠ACB.
46.(1)证明:连接DE,如图1,
∵AB=AC,AD=BD,
∴∠B=∠BAD,∠B=∠C,
∴∠C=∠E,
∴∠E=∠BAD,
∵AE是⊙O的直径,
∴∠ADE=90°,
∴∠E+∠DAE=90°,
∴∠BAD+∠DAE=90°,
即∠BAE=90°,
∴AE⊥AB,
∴直线AB是⊙O的切线;
(2)解:如图2,作AH⊥BC,垂足为点H,
∵AB=AC,
∴BH=CH,
∵∠B=∠C=∠BAD,
∴△ABC∽△DBA,
∴,
即AB2=BD?BC,
又AB=2,BD=AD=3,
∴BC=8,
在Rt△ABH中,BH=CH=4,
∴AH===2,
∵∠E=∠B,∠ADE=∠AHB,
∴△AED∽△ABH,
∴,
∴=3.
47.解:(1)①连接OB,过点B作BT⊥x轴于T,如图1①,
∵⊙O的半径为2,点A(0,1),
∴d(A,⊙O)=2﹣1=1.
∵B(4,3),
∴OB==5,
∴d(B,⊙O)=5﹣2=3.
故答案为:1,3;
②设直线l:y=x+b与x轴、y轴分别交于点P、Q,过点O作OH⊥PQ于H,设OH与⊙O交于点G,如图1②,
∴P(﹣b,0),Q(0,b),
∴OP=|b|,OQ=|b|,
∴PQ=|b|.
∵S△OPQ=OP?OQ=PQ?OH,
∴OH==|b|.
∵直线l:y=x+b与⊙O的密距d(l,⊙O)=,
∴|b|=2+=,
∴b=±4;
(2)过点C作CN⊥DE于N,如图2.
∵点D、E分别是直线y=﹣x+与x轴、y轴的交点,
∴D(4,0),E(0,),
∴OD=4,OE=,
∴tan∠ODE==,
∴∠ODE=30°.
①当点C在点D左边时,m<4.
∵OC=m,
∴CD=4﹣m,
∴CN=CD?sin∠CDN=(4﹣m)=2﹣m.
∵线段DE与⊙C的密距d(DE,⊙C)<,
∴0<2﹣m<+1,
∴1<m<4;
②当点C与点D重合时,m=4.
此时d(DE,⊙C)=0.
③当点C在点D的右边时,m>4.
∵线段DE与⊙C的密距d(DE,⊙C)<,
∴CD﹣1<,
∴(m﹣4)<+1,
∴m<,
∴4<m<.
综上所述:1<m<.
48.解:(1)如图1,连接EC,AC.
∵A(﹣1,0),E(1,0),
∴OA=OE=1,
∴AE=CE=2
∵OE=1,
∴OC===,
∴C(0,),
∵CO⊥AE,OA=OE,
∴CA=CE,
∴CA=CE=AE,
∴△ACE是等边三角形,
∴∠AEC=60°,
∴∠P=∠AEC=30°.
(2)不发生变化.
如图2,连接CB,则∠CPA=∠CBA=∠ACO,
∵∠ACQ=∠ACO+∠OCQ,∠AQC=∠CPA+∠PCQ,
∵CQ平分∠PCD,
∴∠PCQ=∠OCQ,
∴∠ACQ=∠AQC,得AQ=AC=2;
(3)结论①不变,在PD的延长线上截取DM=PC,则PC+PD=PM,
如图3,连接AM,
在△PAC和△MAD中,
,
∴△PAC≌△MAD(SAS),
∴MA=PA,∠MAP=∠DAC=120°,
∴△PAM是以30°为底角的等腰三角形,
过点A作AK⊥PM于K,则MK=PK=AM?cos30°=AM,
∴PM=PA,
∴==.
49.(1)证明:如图①中,连接BI.
∵DB=DI,
∴∠DBI=∠DIB,
∵∠DIB=∠IAB+∠IBA,∠DBI=∠IBC+∠DBC,
又∵∠DBC=∠DAC=∠DAB,
∴∠DBC=∠IAB,
∴∠IBA=∠IBC,即BI平分∠ABC,
∴点I是△ABC的内心.
(2)证明:如图②中,
∵∠BDA=∠BCA,∠DBC=∠DAC,
∴△BDE∽△ACE,
∴=,
∵DB=DI,
∴=.
(3)解:如图③中,作∠BAC的角平分线AD交⊙O于D,连接BD,DC,以D为圆心,DB为半径作作弧,交AD于点I,
由(1)点I是△ABC的内心.
∵IH⊥AC,
∴IH是△ABC的内切圆的半径,
在△AIH中,∠IAH=∠BAC=60°,
∴IH=AI,故欲求IH的最大值只要求出AI的最大值,
∵∠DBC=∠DAC=60°,∠DCB=∠DAB=60°,
∴△BDC是等边三角形,
∴DB=CB=8,即DI=8,
作直径DF,
在Rt△BDF中,∠DFB=60°,DB=8,
∴DF=,即直径为,
∴AI的最大值为﹣8,
∴△ABC的内切圆的半径的最大值为8﹣4.
50.解:(1)∵点A(40,0),点B(0,30),
∴OA=40,OB=30,
∴AC=AO﹣OC=40﹣4t,AF=AP+PF=5t+3t=8t.
故答案为:40﹣4t,8t.
(2)∵CE=6,CD=8,OA=30,OB=40,
∴==,
∵∠DCE=∠AOB=∠DCE=90°,
∴△DCE∽△AOB,
∴∠D=∠BAO,
在Rt△CDE中,DH=ED,
∴CH=DH=EH,
∴∠HCE=∠HEC,
∴∠HCE+∠BAO=∠HEC+∠D=90°,
∴∠AFC=90°,
∵∠AFC=∠AOB=90°,∠FAC=∠OAB,
∴△AF∽△AOB,
∴=,
∴=,
∴t=.
(3)过点P作PM⊥OA于M,则PA=5t,PM=3t,AM=4t,
∴⊙P与x轴相切,
①如图③﹣1中,当⊙P在直线CD的右侧时,设直线CD与⊙P相切于点N,连接PN,则四边形PMCN是正方形.
∴CM=PM,
∴40﹣4t﹣4t=3t,
∴t=.
②如图③﹣2中,当⊙P在直线CD的左侧时,则有40﹣4t=4t﹣3t,解得t=8.
综上所述,当t=或8时,⊙P与CD所在直线及x轴同时相切.
