北师大版七年级数学下册 1.6 完全平方公式 同步测试题(word解析版)
文档属性
| 名称 | 北师大版七年级数学下册 1.6 完全平方公式 同步测试题(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 67.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 13:56:28 | ||
图片预览


文档简介
1.6
完全平方公式
同步测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
1.
用配方法将二次三项式变形,结果是(
)
A.
B.
C.
D.
?
2.
若是一个完全平方式,则的值为(
)
A.
B.
C.
D.
?
3.
用完全平方公式计算的最佳选择是(????????)
A.
B.
C.
D.
?
4.
如果是一个完全平方式,则的值是(?
?
?
?
)
A.
B.
C.
D.
?
5.
如图,将完全相同的四个长方形纸片拼成一个大的正方形,用两种不同的方法表示这个大正方形的面积,则可以得出一个等式为(
)
A.
B.
C.
D.
?6.
用张边长为的正方形纸片,张边长分别为、的矩形纸片,张边长为的正方形纸片,正好拼成一个大正方形(按原纸张进行无空隙、无重叠拼接),则拼成的大正方形边长为(
)
A.
B.
C.
D.
?
7.
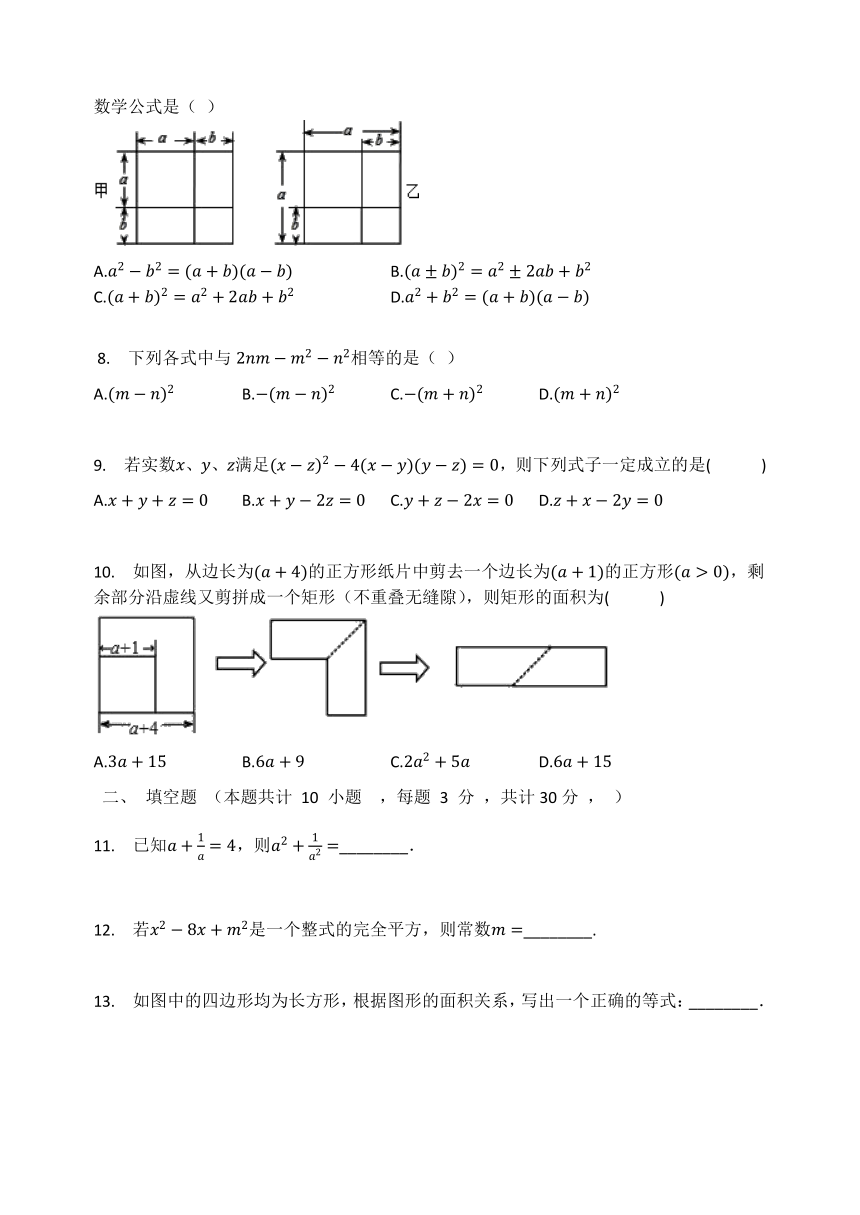
利用图形中面积的等量关系可以得到某些数学公式.例如,根据图甲、乙我们可以得数学公式是(
)
A.
B.
C.
D.
?8.
下列各式中与相等的是(
)
A.
B.
C.
D.
?
9.
若实数、、满足,则下列式子一定成立的是(?
?
?
?
)
A.
B.
C.
D.
?
10.
如图,从边长为的正方形纸片中剪去一个边长为的正方形,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为(?
?
?
?
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
已知,则________.
?
12.
若是一个整式的完全平方,则常数________.
?
13.
如图中的四边形均为长方形,根据图形的面积关系,写出一个正确的等式:________.
?
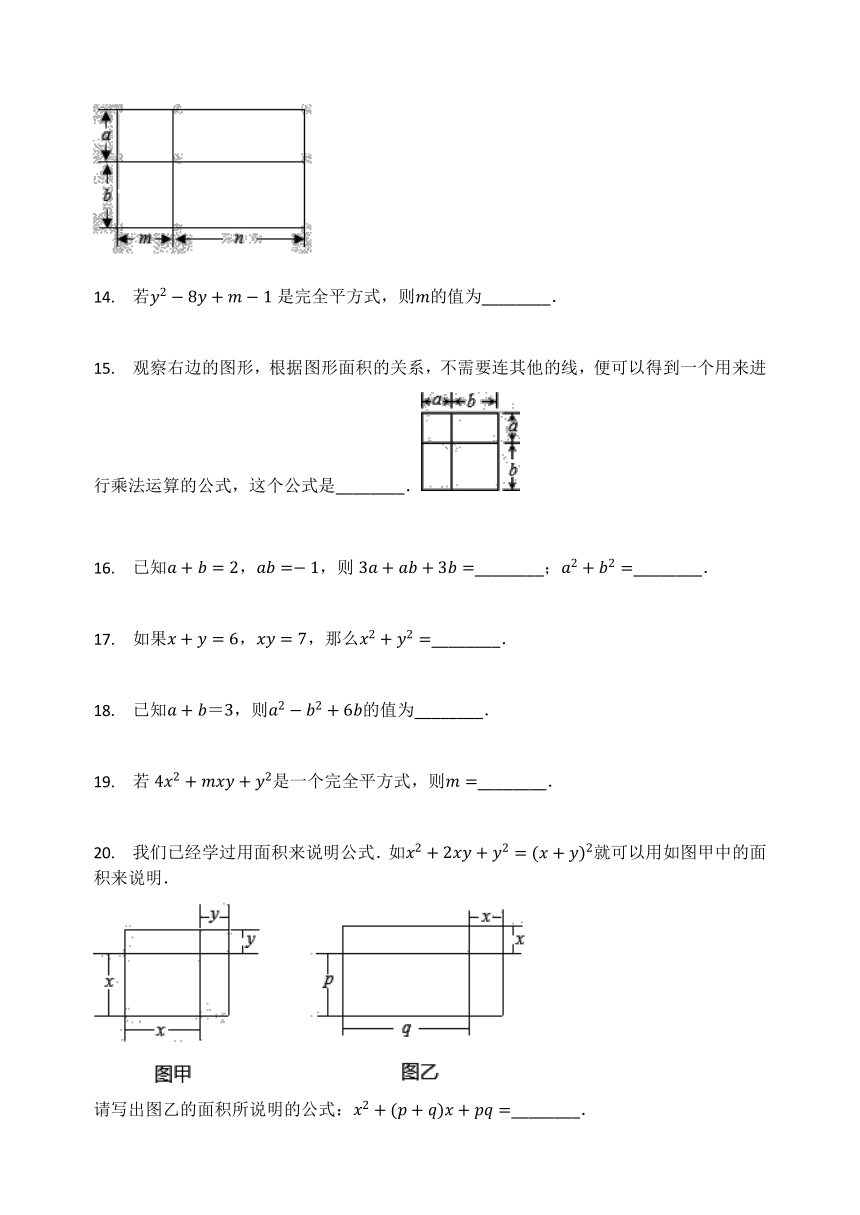
14.
若是完全平方式,则的值为________.
?
15.
观察右边的图形,根据图形面积的关系,不需要连其他的线,便可以得到一个用来进行乘法运算的公式,这个公式是________.
?
16.
已知,,则________;________.
?
17.
如果,,那么________.
?
18.
已知=,则的值为________.
?
19.
若是一个完全平方式,则________.
?
20.
我们已经学过用面积来说明公式.如就可以用如图甲中的面积来说明.
请写出图乙的面积所说明的公式:________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
已知,,求下列各式的值.
;
.
?
22.
已知长方形的周长为,它两邻边长分别为,,且满足,求其面积.
?
23.
有-块边长为的正方形空地,现准备将这块空地的四周均留出宽修筑围坝,中间建喷水池.请计算出喷水池的面积.
?
24.
用四个完全相同的直角三角形(如图)拼成一大一小两个正方形(如图),直角三角形的两直角边分别是、,斜边长为,请解答:
(1)图中间小正方形的周长________,大正方形的边长为________.
(2)用两种方法表示图正方形的面积.(用含,,)=________.
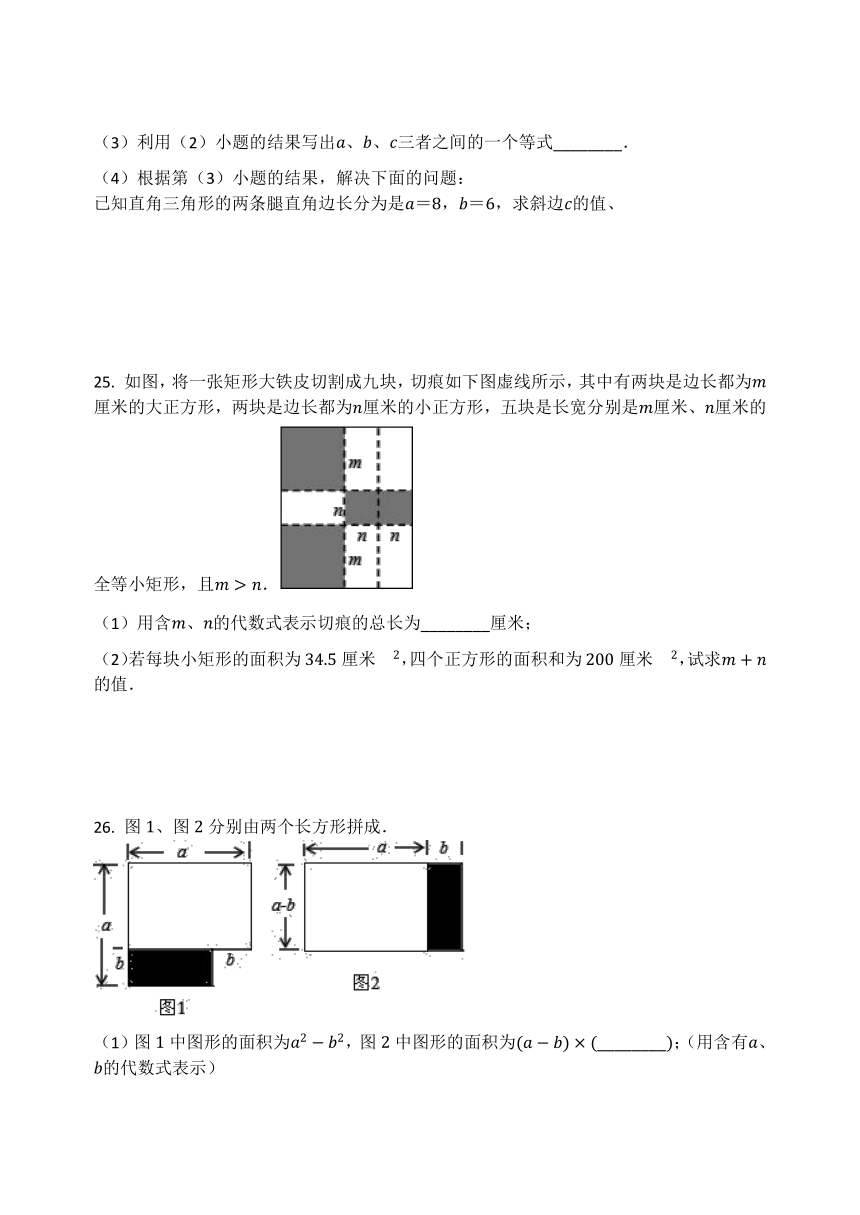
(3)利用(2)小题的结果写出、、三者之间的一个等式________.
(4)根据第(3)小题的结果,解决下面的问题:
已知直角三角形的两条腿直角边长分为是=,=,求斜边的值、
?
25.
如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为厘米的大正方形,两块是边长都为厘米的小正方形,五块是长宽分别是厘米、厘米的全等小矩形,且.
(1)用含、的代数式表示切痕的总长为________厘米;
(2)若每块小矩形的面积为厘米,四个正方形的面积和为厘米,试求的值.
?
26.
图、图分别由两个长方形拼成.
(1)图中图形的面积为,图中图形的面积为________;(用含有、的代数式表示)
(2)由(1)可以得到等式:________;
(3)根据你得到的等式解决下列问题:
①计算:②若=,求的值.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
A
【解答】
解:∵
,
∴
.
故选.
2.
【答案】
D
【解答】
解:∵
是一个完全平方式,
∴
,
故选
3.
【答案】
A
【解答】
略
4.
【答案】
D
【解答】
解:∵
,
∴
.
故选.
5.
【答案】
D
【解答】
解:由图形可得:大正方形的边长为:,则其面积为:,
小正方形的边长为:,则其面积为:,长方形面积为:,
故.
故选.
6.
【答案】
D
【解答】
解:张边长为的正方形纸片的面积是,
张边长分别为、的矩形纸片的面积是,
张边长为的正方形纸片的面积是,
∵
,
∴
拼成的正方形的边长最长可以为.
故选:.
7.
【答案】
B
【解答】
解:图甲可得,
图乙可得.
故选.
8.
【答案】
B
【解答】
解:原式.
故选.
9.
【答案】
D
【解答】
解:∵
,
∴
,
∴
,
∴
,
∴
,
∴
.
故选.
10.
【答案】
D
【解答】
解:矩形的面积
.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:∵
,
∴
,
∴
,
∴
.
故答案为.
12.
【答案】
【解答】
解:∵
,
是一个整式的完全平方,
∴
,解得.
故答案为:.
13.
【答案】
=
【解答】
由图形面积的不同计算方法可得,=;
14.
【答案】
【解答】
解:∵
,
∴
,
解得.
故答案为:.
15.
【答案】
【解答】
解:由图知,大正方形的边长为,
∴
大正方形的面积为,,
根据图知,大正方形分为:一个边长为的小正方形,一个边长为的小正方形,
两个长为,宽为的长方形,
∵
大正方形的面积等于这四部分面积的和,
∴
,
故答案为:.
16.
【答案】
,
【解答】
解:∵
,,
∴
;
.
故答案为:;.
17.
【答案】
【解答】
解:将两边平方得:,
把代入得:,
则.
故答案为:.
18.
【答案】
【解答】
=
=
=
=
=.
19.
【答案】
【解答】
解:∵
,
∴
,
解得.
故答案为:.
20.
【答案】
【解答】
解:根据题意可知,
.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:,,
.
,,
.
【解答】
解:,,
.
,,
.
22.
【答案】
长方形的面积为.
【解答】
解:由题意得:,
解得:①;
∵
,
∴
②.
联立①②成方程组,
解得:,
∴
长方形面积.
23.
【答案】
或.
【解答】
解:喷泉水池的面积为:或.
24.
【答案】
,
或
=
∵
===,
∴
=(负值不合题意,舍去).
【解答】
图中间小正方形的周长,大正方形的边长为,
故答案为:;;
图正方形的面积=或=,
故答案为:或;
∵
=,
∴
=.
故答案为:=
∵
===,
∴
=(负值不合题意,舍去).
25.
【答案】
;
(2)依题意得,,,
∴
,
∵
,
∴
,
∵
,
∴
.
【解答】
解:(1)根据已知图象切痕如图虚线所示直接得出:切痕的总长为;
(2)依题意得,,,
∴
,
∵
,
∴
,
∵
,
∴
.
26.
【答案】
=
①===;
②=
=
=
=
=.
【解答】
图中图形的面积为,图中图形的面积为,
故答案为:;
根据两个图形的面积相等可得=,
故答案为:=;
①===;
②=
=
=
=
=.
完全平方公式
同步测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
1.
用配方法将二次三项式变形,结果是(
)
A.
B.
C.
D.
?
2.
若是一个完全平方式,则的值为(
)
A.
B.
C.
D.
?
3.
用完全平方公式计算的最佳选择是(????????)
A.
B.
C.
D.
?
4.
如果是一个完全平方式,则的值是(?
?
?
?
)
A.
B.
C.
D.
?
5.
如图,将完全相同的四个长方形纸片拼成一个大的正方形,用两种不同的方法表示这个大正方形的面积,则可以得出一个等式为(
)
A.
B.
C.
D.
?6.
用张边长为的正方形纸片,张边长分别为、的矩形纸片,张边长为的正方形纸片,正好拼成一个大正方形(按原纸张进行无空隙、无重叠拼接),则拼成的大正方形边长为(
)
A.
B.
C.
D.
?
7.
利用图形中面积的等量关系可以得到某些数学公式.例如,根据图甲、乙我们可以得数学公式是(
)
A.
B.
C.
D.
?8.
下列各式中与相等的是(
)
A.
B.
C.
D.
?
9.
若实数、、满足,则下列式子一定成立的是(?
?
?
?
)
A.
B.
C.
D.
?
10.
如图,从边长为的正方形纸片中剪去一个边长为的正方形,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为(?
?
?
?
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
已知,则________.
?
12.
若是一个整式的完全平方,则常数________.
?
13.
如图中的四边形均为长方形,根据图形的面积关系,写出一个正确的等式:________.
?
14.
若是完全平方式,则的值为________.
?
15.
观察右边的图形,根据图形面积的关系,不需要连其他的线,便可以得到一个用来进行乘法运算的公式,这个公式是________.
?
16.
已知,,则________;________.
?
17.
如果,,那么________.
?
18.
已知=,则的值为________.
?
19.
若是一个完全平方式,则________.
?
20.
我们已经学过用面积来说明公式.如就可以用如图甲中的面积来说明.
请写出图乙的面积所说明的公式:________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
已知,,求下列各式的值.
;
.
?
22.
已知长方形的周长为,它两邻边长分别为,,且满足,求其面积.
?
23.
有-块边长为的正方形空地,现准备将这块空地的四周均留出宽修筑围坝,中间建喷水池.请计算出喷水池的面积.
?
24.
用四个完全相同的直角三角形(如图)拼成一大一小两个正方形(如图),直角三角形的两直角边分别是、,斜边长为,请解答:
(1)图中间小正方形的周长________,大正方形的边长为________.
(2)用两种方法表示图正方形的面积.(用含,,)=________.
(3)利用(2)小题的结果写出、、三者之间的一个等式________.
(4)根据第(3)小题的结果,解决下面的问题:
已知直角三角形的两条腿直角边长分为是=,=,求斜边的值、
?
25.
如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为厘米的大正方形,两块是边长都为厘米的小正方形,五块是长宽分别是厘米、厘米的全等小矩形,且.
(1)用含、的代数式表示切痕的总长为________厘米;
(2)若每块小矩形的面积为厘米,四个正方形的面积和为厘米,试求的值.
?
26.
图、图分别由两个长方形拼成.
(1)图中图形的面积为,图中图形的面积为________;(用含有、的代数式表示)
(2)由(1)可以得到等式:________;
(3)根据你得到的等式解决下列问题:
①计算:②若=,求的值.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
A
【解答】
解:∵
,
∴
.
故选.
2.
【答案】
D
【解答】
解:∵
是一个完全平方式,
∴
,
故选
3.
【答案】
A
【解答】
略
4.
【答案】
D
【解答】
解:∵
,
∴
.
故选.
5.
【答案】
D
【解答】
解:由图形可得:大正方形的边长为:,则其面积为:,
小正方形的边长为:,则其面积为:,长方形面积为:,
故.
故选.
6.
【答案】
D
【解答】
解:张边长为的正方形纸片的面积是,
张边长分别为、的矩形纸片的面积是,
张边长为的正方形纸片的面积是,
∵
,
∴
拼成的正方形的边长最长可以为.
故选:.
7.
【答案】
B
【解答】
解:图甲可得,
图乙可得.
故选.
8.
【答案】
B
【解答】
解:原式.
故选.
9.
【答案】
D
【解答】
解:∵
,
∴
,
∴
,
∴
,
∴
,
∴
.
故选.
10.
【答案】
D
【解答】
解:矩形的面积
.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:∵
,
∴
,
∴
,
∴
.
故答案为.
12.
【答案】
【解答】
解:∵
,
是一个整式的完全平方,
∴
,解得.
故答案为:.
13.
【答案】
=
【解答】
由图形面积的不同计算方法可得,=;
14.
【答案】
【解答】
解:∵
,
∴
,
解得.
故答案为:.
15.
【答案】
【解答】
解:由图知,大正方形的边长为,
∴
大正方形的面积为,,
根据图知,大正方形分为:一个边长为的小正方形,一个边长为的小正方形,
两个长为,宽为的长方形,
∵
大正方形的面积等于这四部分面积的和,
∴
,
故答案为:.
16.
【答案】
,
【解答】
解:∵
,,
∴
;
.
故答案为:;.
17.
【答案】
【解答】
解:将两边平方得:,
把代入得:,
则.
故答案为:.
18.
【答案】
【解答】
=
=
=
=
=.
19.
【答案】
【解答】
解:∵
,
∴
,
解得.
故答案为:.
20.
【答案】
【解答】
解:根据题意可知,
.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:,,
.
,,
.
【解答】
解:,,
.
,,
.
22.
【答案】
长方形的面积为.
【解答】
解:由题意得:,
解得:①;
∵
,
∴
②.
联立①②成方程组,
解得:,
∴
长方形面积.
23.
【答案】
或.
【解答】
解:喷泉水池的面积为:或.
24.
【答案】
,
或
=
∵
===,
∴
=(负值不合题意,舍去).
【解答】
图中间小正方形的周长,大正方形的边长为,
故答案为:;;
图正方形的面积=或=,
故答案为:或;
∵
=,
∴
=.
故答案为:=
∵
===,
∴
=(负值不合题意,舍去).
25.
【答案】
;
(2)依题意得,,,
∴
,
∵
,
∴
,
∵
,
∴
.
【解答】
解:(1)根据已知图象切痕如图虚线所示直接得出:切痕的总长为;
(2)依题意得,,,
∴
,
∵
,
∴
,
∵
,
∴
.
26.
【答案】
=
①===;
②=
=
=
=
=.
【解答】
图中图形的面积为,图中图形的面积为,
故答案为:;
根据两个图形的面积相等可得=,
故答案为:=;
①===;
②=
=
=
=
=.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
