人教版九年级上册第二十三章-旋转教案
图片预览

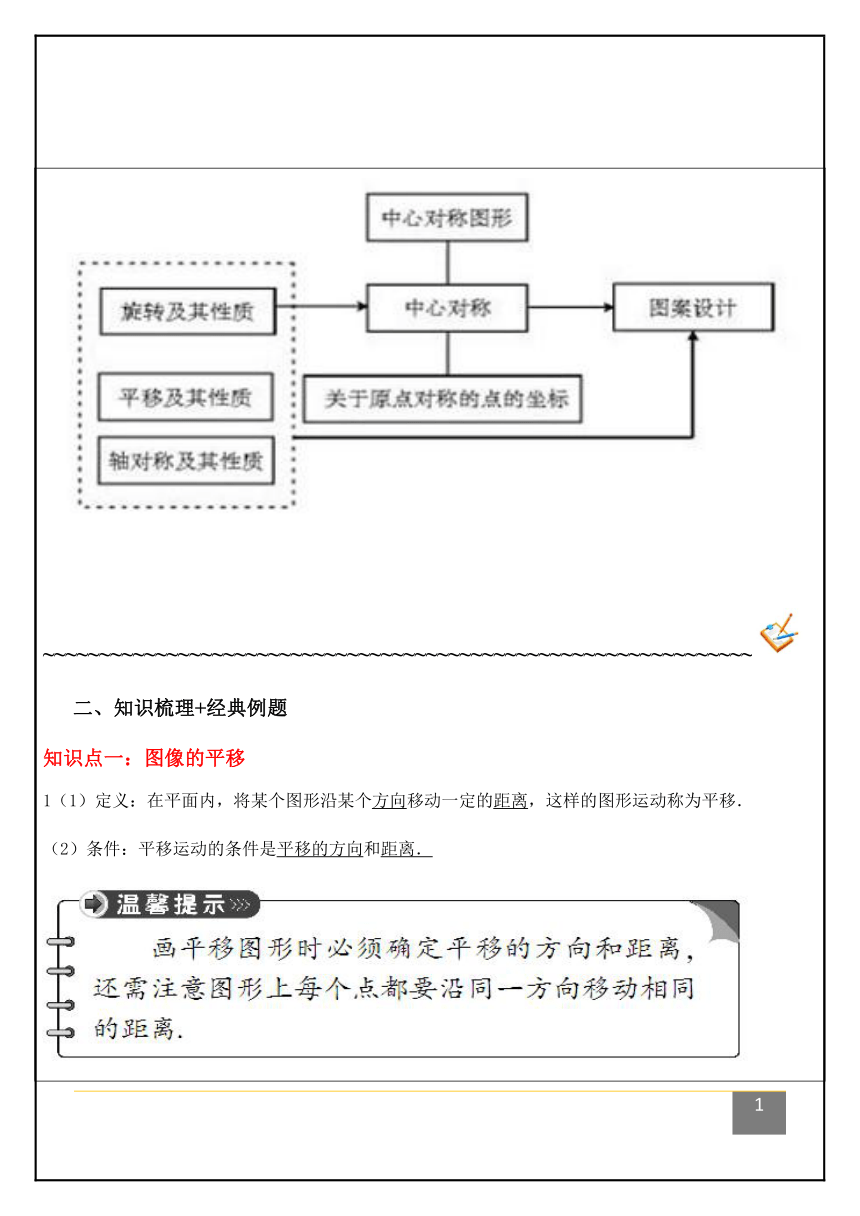



文档简介
学员编号:
年
级:
课时数:
第
次课
学员姓名:
辅导科目:
学科教师:
班主任:
授课日期及时段
年
月
日
时
分
——
时
分
授课主题
旋转及概率初步
教学目标
1、对生活中的旋转现象认识过程的体验
2、旋转内容的理解掌握.?
3、旋转性质的掌握与运用
重点难点
1、旋转的性质?
2、中心对称图形与中心对称
3、与旋转有关的计算
教学内容
一、导入
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
二、知识梳理+经典例题
知识点一:图像的平移
1(1)定义:在平面内,将某个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
(2)条件:平移运动的条件是平移的方向和距离.
2、平移的性质
(1)平移不改变图形的形状与大小,即平移后所得的新图形与原图形全等;
(2)连接各组对应点的线段长度相等;
(3)对应线段所在的直线相互平行或重合;
(4)对应角相等.
例1:在如图所示的平面直角坐标系内,画在透明胶片上的?ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(5,-1)处,则此平移可以是( )
A.先向右平移5个单位,再向下平移1个单位
B.先向右平移5个单位,再向下平移3个单位
C.先向右平移4个单位,再向下平移1个单位
D.先向右平移4个单位,再向下平移3个单位
知识点二:图形的旋转
1.旋转的定义:在平面内,将一个图形绕一个定点沿某个方向转动一定角度,这样的图形变换称为旋转,这个定点称为旋转中心,转动的角称为旋转角.
注意:在旋转过程中保持不动的点是旋转中心.
注:(1)弄清旋转中心在哪,旋转的角度多大,旋转方向是顺时针还是逆时针;
(2)图上的对应点与图形具有相同的旋转方向和旋转角度。
2.旋转的三个要素:
旋转中心、旋转的角度和方向.
3.旋转的性质:
(1)对应点到旋转中心的距离相等;
(2)对应点与旋转中心所连线段的夹角等于旋转角;
(3)旋转前后的图形全等.
如图所示,将OBA绕着O点按逆时针方向旋转,得到OBA’,我们可以发现:OA=OA’
,OB=OB’
,
AB=AB’
,OBA=OBA’
,AOB=AOB’
,
OAB=OAB’.
注意:与对称轴、平移相同,旋转只改变图形的位置,不改变图形的形状和大小。
例2:如图所示,点A,B,C,D都在方格纸的格点上,若三角形AOB绕点O按逆时针方向旋转到三角形COD的位置,则旋转的角度为:
知识巩固:如图,该五角星绕点O按下列角度旋转后,不能与其自身重合的是(
)
A.
72度
B.108度
C.144度
D
.216度
知识点三:中心对称图形与中心对称
1、中心对称图形:如果把一个图形绕着某一点旋转180度后能与自身重合,那么我们就说,这个图形成中心对称图形。
2、中心对称:如果把一个图形绕着某一点旋转180度后能与另一个图形重合,那么我们就说,这两个图形成中心对称。
3、中心对称和中心对称图形的区别
中心对称是指两个全等图形之间的相互位置关系,这两个图形关于一点对称,这个点是对称中心,两个图形关于点的对称也叫做中心对称.成中心对称的两个图形中,其中一个上所有点关于对称中心的对称点都在另一个图形上,反之,另一个图形上所有点的对称点,又都在这个图形上;而中心对称图形是指一个图形本身成中心对称.中心对称图形上所有点关于对称中心的对称点都在这个图形本身上。
如果将中心对称的两个图形看成一个整体(一个图形),那么这个图形就是中心对称图形;一个中心对称图形,如果把对称的部分看成是两个图形,那么它们又是关于中心对称。
例3:下列图形中,中心对称图形是
(
)
A
B
C
D
知识巩固:下列图形中,既是中心对称又是轴对称的图形是(
)
知识点四:中心对称的性质
1、性子:(1)关于中心对称的两个图形是全等形。?
(2)关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。?
(3)关于中心对称的两个图形,对应线段平行(或者在同一直线上)且相等。
2、坐标系中对称点的特征
(1)关于原点对称的点的特征:两个点关于原点对称时,它们的坐标的符号相反,即点P(x,y)关于原点的对称点为P’(-x,-y)?
(2)关于x轴对称的点的特征:两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y)?
(3)关于y轴对称的点的特征:两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y)
例4:在平面直角坐标系中,A点坐标为(3,4),将OA绕原点O逆时针旋转900得到OA?,则点A?的坐标是(
)
A、(-4,3)
B、(-3,4)
C、(3,-4)
D、(4,-3)
知识巩固:如图,△ABC中,∠BAC=120°,以BC为边向外作等边△BCD,把△ABD绕着点D按顺时针方向旋转60°到△ECD的位置,若AB=3,AC=2,求∠BAD的度数和AD的长.
知识点五:与旋转有关的计算及作图
1、关于中心对称的作图:
(1)确定对称中心;(2)确定关键点;(3)作关键点的关于对称中心的对称点;(4)连结各点,得到所需图形.
2、旋转的性质:(1)关于中心对称的两个图形是全等形。?(2)关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。?(3)关于中心对称的两个图形,对应线段平行(或者在同一直线上)且相等。
例5:将△ABC绕着点C按顺时针方向旋转20°,B点落在B′位置,A点落在A′位置,
若AC⊥A′B′,则∠BAC的度数是(
)
A.50°
B.60°
C.70°
D.80°
三、随堂检测
一、选择题
1.下列图形中,是中心对称图形的是( )
2.以下图的右边缘所在直线为轴将该图案向右翻折后,再绕中心旋转180°,所得到的图形是( )
3.用数学的方式理解“当窗理云鬓,对镜贴花黄”和“坐地日行八万里”(只考虑地球的自转),其中蕴含的图形运动是( )
A.平移和旋转
B.对称和旋转
C.对称和平移
D.旋转和平移
4.已知点A(a,2013)与点A′(﹣2014,b)是关于原点O的对称点,则a+b的值为( )
A.1
B.5
C.6
D.4
5.在平面直角坐标系中,若点P(m,m﹣n)与点Q(﹣2,3)关于原点对称,则点M(m,n)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.如图是一个标准的五角星,若将它绕旋转中心旋转一定角度后能与自身重合,则至少应将它旋转的度数是( )
A.60°
B.72°
C.90°
D.144°
7.如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是( )
A.50°
B.60°
C.40°
D.30°
8.在平面直角坐标系xOy中,A点坐标为(3,4),将OA绕原点O顺时针旋转180°得到OA′,则点A′的坐标是( )
A.(﹣4,3)
B.(﹣3,﹣4)
C.(﹣4,﹣3)
D.(﹣3,4)
9.如图,将Rt△ABC(其中∠B=30°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点B、A、B1在同一条直线上,那么旋转角等于( )
A.30°
B.60°
C.90°
D.180°
10.如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE,连接BD,若AC=3,DE=1,则线段BD的长为( )
A.2
B.2
C.4
D.2
二、填空题
11.如图,△ABC中,∠C=30°,将△ABC绕点A顺时针旋转60°得△ADE,AE与BC交于F,则∠AFB=_______°.
12.如图,把Rt△ABC绕点A逆时针旋转44°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=
图11
图12
13.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,2),则点B2016的坐标为
.
14.如图,直线y=﹣x+2与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△AO′B′,则点B′的坐标是
.
15.时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的旋转角是
.
16.在等腰三角形ABC中,∠C=90°,BC=2cm,如果以AC的中点O为旋转中心,将△ABC旋转180°,点B落在B′处,则BB′的长度为
.
三、解答题
17.如图,说出这个图形的旋转中心,它绕旋转中心至少旋转多大角度才能与原来图形重合?
18.将下图所示的图形面积分成相等的两部分.(图中圆圈为挖去部分)
19.(8分)直角坐标系第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,试求x+2y的值.
如图,已知AD=AE,AB=AC.(1)求证:∠B=∠C;
(2)若∠A=50°,问△ADC经过怎样的变换能与△AEB重合?
21.如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴,垂足为A.
(1)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标;
(2)△O′A′B′与△OAB关于原点对称,写出点B′、A′的坐标.
22.当m为何值时
(1)点A(2,3m)关于原点的对称点在第三象限;
(2)点B(3m﹣1,0.5m+2)到x轴的距离等于它到y轴距离的一半?
23.直角坐标系中,已知点P(﹣2,﹣1),点T(t,0)是x轴上的一个动点.
(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时,△P′TO是等腰三角形?
24.等边△OAB在平面直角坐标系中,已知点A(2,0),将△OAB绕点O顺时针方向旋转a°(0<a<360)得△OA1B1.
(1)求出点B的坐标;
(2)当A1与B1的纵坐标相同时,求出a的值;
(3)在(2)的条件下直接写出点B1的坐标.
7
年
级:
课时数:
第
次课
学员姓名:
辅导科目:
学科教师:
班主任:
授课日期及时段
年
月
日
时
分
——
时
分
授课主题
旋转及概率初步
教学目标
1、对生活中的旋转现象认识过程的体验
2、旋转内容的理解掌握.?
3、旋转性质的掌握与运用
重点难点
1、旋转的性质?
2、中心对称图形与中心对称
3、与旋转有关的计算
教学内容
一、导入
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
二、知识梳理+经典例题
知识点一:图像的平移
1(1)定义:在平面内,将某个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
(2)条件:平移运动的条件是平移的方向和距离.
2、平移的性质
(1)平移不改变图形的形状与大小,即平移后所得的新图形与原图形全等;
(2)连接各组对应点的线段长度相等;
(3)对应线段所在的直线相互平行或重合;
(4)对应角相等.
例1:在如图所示的平面直角坐标系内,画在透明胶片上的?ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(5,-1)处,则此平移可以是( )
A.先向右平移5个单位,再向下平移1个单位
B.先向右平移5个单位,再向下平移3个单位
C.先向右平移4个单位,再向下平移1个单位
D.先向右平移4个单位,再向下平移3个单位
知识点二:图形的旋转
1.旋转的定义:在平面内,将一个图形绕一个定点沿某个方向转动一定角度,这样的图形变换称为旋转,这个定点称为旋转中心,转动的角称为旋转角.
注意:在旋转过程中保持不动的点是旋转中心.
注:(1)弄清旋转中心在哪,旋转的角度多大,旋转方向是顺时针还是逆时针;
(2)图上的对应点与图形具有相同的旋转方向和旋转角度。
2.旋转的三个要素:
旋转中心、旋转的角度和方向.
3.旋转的性质:
(1)对应点到旋转中心的距离相等;
(2)对应点与旋转中心所连线段的夹角等于旋转角;
(3)旋转前后的图形全等.
如图所示,将OBA绕着O点按逆时针方向旋转,得到OBA’,我们可以发现:OA=OA’
,OB=OB’
,
AB=AB’
,OBA=OBA’
,AOB=AOB’
,
OAB=OAB’.
注意:与对称轴、平移相同,旋转只改变图形的位置,不改变图形的形状和大小。
例2:如图所示,点A,B,C,D都在方格纸的格点上,若三角形AOB绕点O按逆时针方向旋转到三角形COD的位置,则旋转的角度为:
知识巩固:如图,该五角星绕点O按下列角度旋转后,不能与其自身重合的是(
)
A.
72度
B.108度
C.144度
D
.216度
知识点三:中心对称图形与中心对称
1、中心对称图形:如果把一个图形绕着某一点旋转180度后能与自身重合,那么我们就说,这个图形成中心对称图形。
2、中心对称:如果把一个图形绕着某一点旋转180度后能与另一个图形重合,那么我们就说,这两个图形成中心对称。
3、中心对称和中心对称图形的区别
中心对称是指两个全等图形之间的相互位置关系,这两个图形关于一点对称,这个点是对称中心,两个图形关于点的对称也叫做中心对称.成中心对称的两个图形中,其中一个上所有点关于对称中心的对称点都在另一个图形上,反之,另一个图形上所有点的对称点,又都在这个图形上;而中心对称图形是指一个图形本身成中心对称.中心对称图形上所有点关于对称中心的对称点都在这个图形本身上。
如果将中心对称的两个图形看成一个整体(一个图形),那么这个图形就是中心对称图形;一个中心对称图形,如果把对称的部分看成是两个图形,那么它们又是关于中心对称。
例3:下列图形中,中心对称图形是
(
)
A
B
C
D
知识巩固:下列图形中,既是中心对称又是轴对称的图形是(
)
知识点四:中心对称的性质
1、性子:(1)关于中心对称的两个图形是全等形。?
(2)关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。?
(3)关于中心对称的两个图形,对应线段平行(或者在同一直线上)且相等。
2、坐标系中对称点的特征
(1)关于原点对称的点的特征:两个点关于原点对称时,它们的坐标的符号相反,即点P(x,y)关于原点的对称点为P’(-x,-y)?
(2)关于x轴对称的点的特征:两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y)?
(3)关于y轴对称的点的特征:两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y)
例4:在平面直角坐标系中,A点坐标为(3,4),将OA绕原点O逆时针旋转900得到OA?,则点A?的坐标是(
)
A、(-4,3)
B、(-3,4)
C、(3,-4)
D、(4,-3)
知识巩固:如图,△ABC中,∠BAC=120°,以BC为边向外作等边△BCD,把△ABD绕着点D按顺时针方向旋转60°到△ECD的位置,若AB=3,AC=2,求∠BAD的度数和AD的长.
知识点五:与旋转有关的计算及作图
1、关于中心对称的作图:
(1)确定对称中心;(2)确定关键点;(3)作关键点的关于对称中心的对称点;(4)连结各点,得到所需图形.
2、旋转的性质:(1)关于中心对称的两个图形是全等形。?(2)关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。?(3)关于中心对称的两个图形,对应线段平行(或者在同一直线上)且相等。
例5:将△ABC绕着点C按顺时针方向旋转20°,B点落在B′位置,A点落在A′位置,
若AC⊥A′B′,则∠BAC的度数是(
)
A.50°
B.60°
C.70°
D.80°
三、随堂检测
一、选择题
1.下列图形中,是中心对称图形的是( )
2.以下图的右边缘所在直线为轴将该图案向右翻折后,再绕中心旋转180°,所得到的图形是( )
3.用数学的方式理解“当窗理云鬓,对镜贴花黄”和“坐地日行八万里”(只考虑地球的自转),其中蕴含的图形运动是( )
A.平移和旋转
B.对称和旋转
C.对称和平移
D.旋转和平移
4.已知点A(a,2013)与点A′(﹣2014,b)是关于原点O的对称点,则a+b的值为( )
A.1
B.5
C.6
D.4
5.在平面直角坐标系中,若点P(m,m﹣n)与点Q(﹣2,3)关于原点对称,则点M(m,n)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.如图是一个标准的五角星,若将它绕旋转中心旋转一定角度后能与自身重合,则至少应将它旋转的度数是( )
A.60°
B.72°
C.90°
D.144°
7.如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是( )
A.50°
B.60°
C.40°
D.30°
8.在平面直角坐标系xOy中,A点坐标为(3,4),将OA绕原点O顺时针旋转180°得到OA′,则点A′的坐标是( )
A.(﹣4,3)
B.(﹣3,﹣4)
C.(﹣4,﹣3)
D.(﹣3,4)
9.如图,将Rt△ABC(其中∠B=30°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点B、A、B1在同一条直线上,那么旋转角等于( )
A.30°
B.60°
C.90°
D.180°
10.如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE,连接BD,若AC=3,DE=1,则线段BD的长为( )
A.2
B.2
C.4
D.2
二、填空题
11.如图,△ABC中,∠C=30°,将△ABC绕点A顺时针旋转60°得△ADE,AE与BC交于F,则∠AFB=_______°.
12.如图,把Rt△ABC绕点A逆时针旋转44°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=
图11
图12
13.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,2),则点B2016的坐标为
.
14.如图,直线y=﹣x+2与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△AO′B′,则点B′的坐标是
.
15.时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的旋转角是
.
16.在等腰三角形ABC中,∠C=90°,BC=2cm,如果以AC的中点O为旋转中心,将△ABC旋转180°,点B落在B′处,则BB′的长度为
.
三、解答题
17.如图,说出这个图形的旋转中心,它绕旋转中心至少旋转多大角度才能与原来图形重合?
18.将下图所示的图形面积分成相等的两部分.(图中圆圈为挖去部分)
19.(8分)直角坐标系第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,试求x+2y的值.
如图,已知AD=AE,AB=AC.(1)求证:∠B=∠C;
(2)若∠A=50°,问△ADC经过怎样的变换能与△AEB重合?
21.如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴,垂足为A.
(1)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标;
(2)△O′A′B′与△OAB关于原点对称,写出点B′、A′的坐标.
22.当m为何值时
(1)点A(2,3m)关于原点的对称点在第三象限;
(2)点B(3m﹣1,0.5m+2)到x轴的距离等于它到y轴距离的一半?
23.直角坐标系中,已知点P(﹣2,﹣1),点T(t,0)是x轴上的一个动点.
(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时,△P′TO是等腰三角形?
24.等边△OAB在平面直角坐标系中,已知点A(2,0),将△OAB绕点O顺时针方向旋转a°(0<a<360)得△OA1B1.
(1)求出点B的坐标;
(2)当A1与B1的纵坐标相同时,求出a的值;
(3)在(2)的条件下直接写出点B1的坐标.
7
同课章节目录
