6.5 一次函数的应用 第1课时 一个一次函数图象的应用(含答案)
文档属性
| 名称 | 6.5 一次函数的应用 第1课时 一个一次函数图象的应用(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 14:15:20 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 一次函数
5 一次函数的应用
第1课时 一个一次函数图象的应用
夯实基础
知识点一 利用图象信息解决实际问题
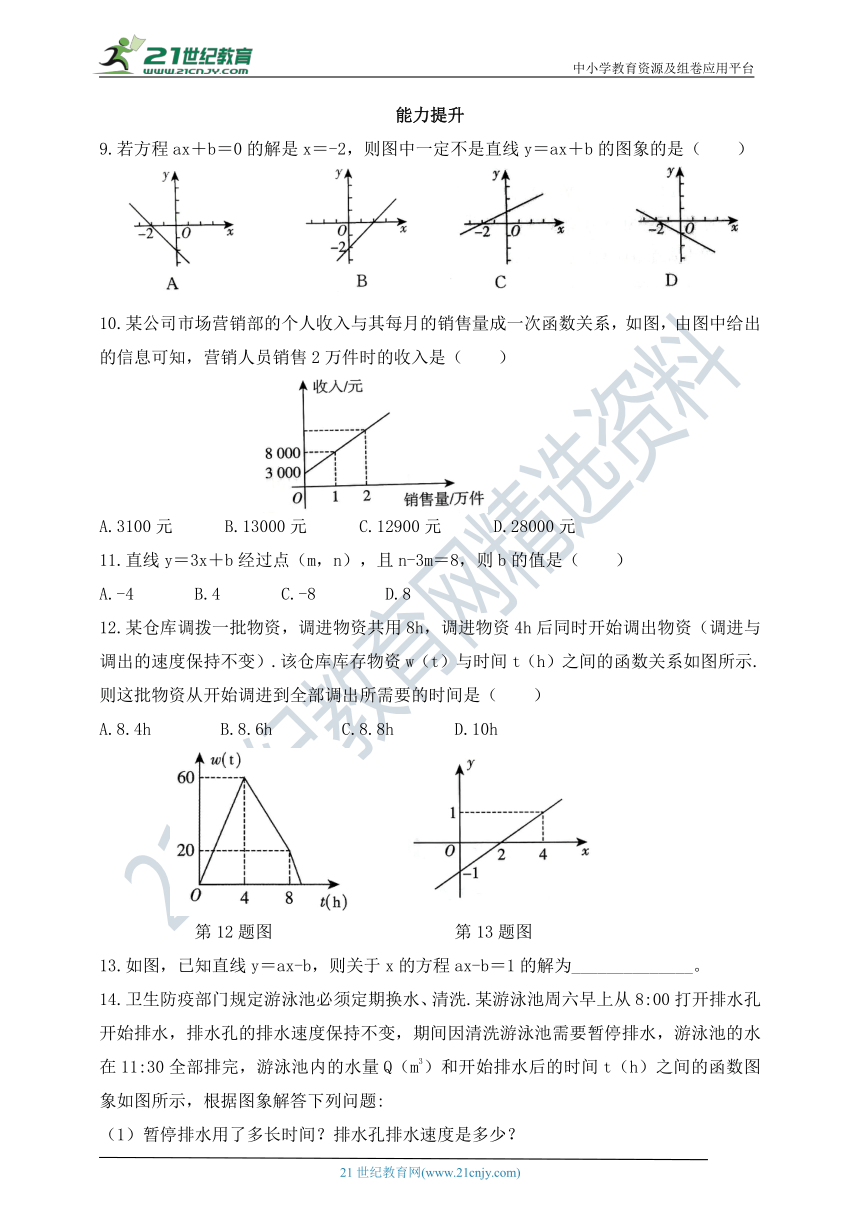
1.小刚以400m/min的速度匀速骑车5min,在原地休息了6min,然后以500m/min的速度骑回出发地.下列函数图象能表达这一过程的是( )
2.某班同学在探究弹簧的长度跟外力的变化关系时,实验记录得到的相应数据如下表:
砝码质量 x(g) 0 50 100 150 200 250 300 400
弹簧长度 y(cm) 2 3 4 5 6 7 7.5 7.5
则y关于x的函数图象是( )
3.某农场租用收割机收割小麦,s(亩)甲收割机单独收割2天后,又调来乙收割机参与收割,直至完成800亩的收割任务,收割亩数与天数之间的函数关系如图所示,那么乙参与收割的天数是__________天。
第3题图 第4题图
4.(上海中考)一辆汽车在某次行驶过程中,油箱中的剩余油量y(L)与行驶路程x(km)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式(不需要写定义域);
(2)已知当油箱中的剩余油量为8L时,该汽车会开始提示加油.在此行驶过程中,行驶了500km时,司机发现离前方最近的加油站有30km的路程,在开往加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?
知识点二 一次函数与一元一次方程的关系
5.如图,直线y=ax+b(a≠0)过点A(0,4),B(-3,0),则方程ax+b=0的解是( )
A.x=-3 B.x=4
C.x=- D.x=-
6.已知一次函数y=ax+b(a,b是常数且a≠0),x与y的部分对应值如下表:
x -2 -1 0 1 2 3
y 6 4 2 0 -2 -4
那么方程ax+b=0的解是( )
A.x=-1 B.x=0 C.x=1 D.x=4
7.若方程x-2=0的解也是直线y=(2k-1)x+10与x轴的交点的横坐标,则k的值为( )
A.2 B.0 C.-2 D.±2
易错点 对自变量或函数值代表的实际意义理解不准确而造成错误
8.汽车由A地驶往相距400km的B地,如果汽车的平均速度是100km/h,那么汽车距B地的距离s(km)与行驶时间t(h)的关系用图象表示应为( )
能力提升
9.若方程ax+b=0的解是x=-2,则图中一定不是直线y=ax+b的图象的是( )
10.某公司市场营销部的个人收入与其每月的销售量成一次函数关系,如图,由图中给出的信息可知,营销人员销售2万件时的收入是( )
A.3100元 B.13000元 C.12900元 D.28000元
11.直线y=3x+b经过点(m,n),且n-3m=8,则b的值是( )
A.-4 B.4 C.-8 D.8
12.某仓库调拨一批物资,调进物资共用8h,调进物资4h后同时开始调出物资(调进与调出的速度保持不变).该仓库库存物资w(t)与时间t(h)之间的函数关系如图所示.则这批物资从开始调进到全部调出所需要的时间是( )
A.8.4h B.8.6h C.8.8h D.10h
第12题图 第13题图
13.如图,已知直线y=ax-b,则关于x的方程ax-b=1的解为______________。
14.卫生防疫部门规定游泳池必须定期换水、清洗.某游泳池周六早上从8:00打开排水孔开始排水,排水孔的排水速度保持不变,期间因清洗游泳池需要暂停排水,游泳池的水在11:30全部排完,游泳池内的水量Q(m3)和开始排水后的时间t(h)之间的函数图象如图所示,根据图象解答下列问题:
(1)暂停排水用了多长时间?排水孔排水速度是多少?
(2)当0≤t≤1.5时,求Q关于t的函数表达式.
素养提升
15.温度与我们的生活息息相关,如图是一个温度计实物示意图,左边的刻度是摄氏温度(℃),右边的刻度是华氏温度(0F).设摄氏温度为x(℃),华氏温度为y(0F),则y是x的一次函数,通过观察我们发现,温度计上的摄氏温度为0℃时,华氏温度为320F;摄氏温度为-20℃时,华氏温度为-40F。
请根据以上信息,解答下列问题:
(1)仔细观察图中数据,试求出y与x的函数关系式;
(2)当摄氏温度为-5℃时,华氏温度为多少?(3)当华氏温度为59F时,摄氏温度为多少?
参考答案
1.C 2.C 3.4
4.解:(1)设一次函数的关系式是y=kx+b,由图象知,
点(0,60)与点(150,45)在此函数图象上,将其代入,得b=60,150k+b=45,
解得k=-.
故y关于x的函数关系式为y=-x+60.
当y=8时,有-x+60=8,解得x=520.30-(520-500)=10(km)。
故汽车开始提示加油时,离加油站的路程是10 km。
5.A 6.C 7.C 8.C 9.B 10.B 11.D 12.C 13.x=4
14.解:(1)由图可得:暂停排水的时间为2-1.5=0.5(h);
排水孔排水速度为900÷(3.5-0.5)=300(m3/h).
所以暂停排水用了0.5h,排水孔排水速度为300m3/h.
(2)设当0≤t≤1.5时,设Q关于t的函数表达式为Q=kt+b,
当t=1.5时,Q=900-300×1.5=450.所以b=900,1.5k+b=450,解得k=-300.
所以当0≤t≤1.5时,Q关于t的函数表达式为Q=-300t+900.
15.解:(1)设y关于x的函数关系式为y=kx+b,
由温度计的示数,得x=0,y=32;x=-20,y=-4.
所以b=32,-20k+b=-4,解得k=.
所以y关于x的函数关系式为y=x+32.
(2)当x=-5时,y=×(-5)+32=23,
所以当摄氏温度为-5℃时,华氏温度为230F.
(3)令y=59,则有x+32=59,解得x=15.所以当华氏温度为590F时,摄氏温度为15℃.
_21?????????è?????(www.21cnjy.com)_
第六章 一次函数
5 一次函数的应用
第1课时 一个一次函数图象的应用
夯实基础
知识点一 利用图象信息解决实际问题
1.小刚以400m/min的速度匀速骑车5min,在原地休息了6min,然后以500m/min的速度骑回出发地.下列函数图象能表达这一过程的是( )
2.某班同学在探究弹簧的长度跟外力的变化关系时,实验记录得到的相应数据如下表:
砝码质量 x(g) 0 50 100 150 200 250 300 400
弹簧长度 y(cm) 2 3 4 5 6 7 7.5 7.5
则y关于x的函数图象是( )
3.某农场租用收割机收割小麦,s(亩)甲收割机单独收割2天后,又调来乙收割机参与收割,直至完成800亩的收割任务,收割亩数与天数之间的函数关系如图所示,那么乙参与收割的天数是__________天。
第3题图 第4题图
4.(上海中考)一辆汽车在某次行驶过程中,油箱中的剩余油量y(L)与行驶路程x(km)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式(不需要写定义域);
(2)已知当油箱中的剩余油量为8L时,该汽车会开始提示加油.在此行驶过程中,行驶了500km时,司机发现离前方最近的加油站有30km的路程,在开往加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?
知识点二 一次函数与一元一次方程的关系
5.如图,直线y=ax+b(a≠0)过点A(0,4),B(-3,0),则方程ax+b=0的解是( )
A.x=-3 B.x=4
C.x=- D.x=-
6.已知一次函数y=ax+b(a,b是常数且a≠0),x与y的部分对应值如下表:
x -2 -1 0 1 2 3
y 6 4 2 0 -2 -4
那么方程ax+b=0的解是( )
A.x=-1 B.x=0 C.x=1 D.x=4
7.若方程x-2=0的解也是直线y=(2k-1)x+10与x轴的交点的横坐标,则k的值为( )
A.2 B.0 C.-2 D.±2
易错点 对自变量或函数值代表的实际意义理解不准确而造成错误
8.汽车由A地驶往相距400km的B地,如果汽车的平均速度是100km/h,那么汽车距B地的距离s(km)与行驶时间t(h)的关系用图象表示应为( )
能力提升
9.若方程ax+b=0的解是x=-2,则图中一定不是直线y=ax+b的图象的是( )
10.某公司市场营销部的个人收入与其每月的销售量成一次函数关系,如图,由图中给出的信息可知,营销人员销售2万件时的收入是( )
A.3100元 B.13000元 C.12900元 D.28000元
11.直线y=3x+b经过点(m,n),且n-3m=8,则b的值是( )
A.-4 B.4 C.-8 D.8
12.某仓库调拨一批物资,调进物资共用8h,调进物资4h后同时开始调出物资(调进与调出的速度保持不变).该仓库库存物资w(t)与时间t(h)之间的函数关系如图所示.则这批物资从开始调进到全部调出所需要的时间是( )
A.8.4h B.8.6h C.8.8h D.10h
第12题图 第13题图
13.如图,已知直线y=ax-b,则关于x的方程ax-b=1的解为______________。
14.卫生防疫部门规定游泳池必须定期换水、清洗.某游泳池周六早上从8:00打开排水孔开始排水,排水孔的排水速度保持不变,期间因清洗游泳池需要暂停排水,游泳池的水在11:30全部排完,游泳池内的水量Q(m3)和开始排水后的时间t(h)之间的函数图象如图所示,根据图象解答下列问题:
(1)暂停排水用了多长时间?排水孔排水速度是多少?
(2)当0≤t≤1.5时,求Q关于t的函数表达式.
素养提升
15.温度与我们的生活息息相关,如图是一个温度计实物示意图,左边的刻度是摄氏温度(℃),右边的刻度是华氏温度(0F).设摄氏温度为x(℃),华氏温度为y(0F),则y是x的一次函数,通过观察我们发现,温度计上的摄氏温度为0℃时,华氏温度为320F;摄氏温度为-20℃时,华氏温度为-40F。
请根据以上信息,解答下列问题:
(1)仔细观察图中数据,试求出y与x的函数关系式;
(2)当摄氏温度为-5℃时,华氏温度为多少?(3)当华氏温度为59F时,摄氏温度为多少?
参考答案
1.C 2.C 3.4
4.解:(1)设一次函数的关系式是y=kx+b,由图象知,
点(0,60)与点(150,45)在此函数图象上,将其代入,得b=60,150k+b=45,
解得k=-.
故y关于x的函数关系式为y=-x+60.
当y=8时,有-x+60=8,解得x=520.30-(520-500)=10(km)。
故汽车开始提示加油时,离加油站的路程是10 km。
5.A 6.C 7.C 8.C 9.B 10.B 11.D 12.C 13.x=4
14.解:(1)由图可得:暂停排水的时间为2-1.5=0.5(h);
排水孔排水速度为900÷(3.5-0.5)=300(m3/h).
所以暂停排水用了0.5h,排水孔排水速度为300m3/h.
(2)设当0≤t≤1.5时,设Q关于t的函数表达式为Q=kt+b,
当t=1.5时,Q=900-300×1.5=450.所以b=900,1.5k+b=450,解得k=-300.
所以当0≤t≤1.5时,Q关于t的函数表达式为Q=-300t+900.
15.解:(1)设y关于x的函数关系式为y=kx+b,
由温度计的示数,得x=0,y=32;x=-20,y=-4.
所以b=32,-20k+b=-4,解得k=.
所以y关于x的函数关系式为y=x+32.
(2)当x=-5时,y=×(-5)+32=23,
所以当摄氏温度为-5℃时,华氏温度为230F.
(3)令y=59,则有x+32=59,解得x=15.所以当华氏温度为590F时,摄氏温度为15℃.
_21?????????è?????(www.21cnjy.com)_
