6.3 第1课时 和差倍分问题、配套问题 课件(共32张ppt)
文档属性
| 名称 | 6.3 第1课时 和差倍分问题、配套问题 课件(共32张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 22:08:53 | ||
图片预览










文档简介
导入新课
讲授新课
当堂练习
课堂小结
6.3 二元一次方程组的应用
第六章 二元一次方程组
第1课时 和差倍分问题、配套问题及行程问题
学习目标
1.能根据具体问题的数量关系,列出二元一次方程组解决和差倍分问题、配套问题及行程问题.(重点、难点)
2.掌握应用二元一次方程组解决实际问题的一般步骤.(重点)
导入新课
情境引入
累死我了!
我还想多给你1包呢!
把我驮的东西给你一包多好哇!这样咱俩驮的包数就一样多了.
那可不行!如果你给我1包,我驮的包数就是你的2倍了.
真的?!
讲授新课
列方程组解决和、差、倍、分问题
一
互动探究
问题1 牛和马的对话中,你能找到哪些等量关系?
(1) 牛驮物的包数-1=马驮物的包数+1;
(2) 牛驮物的包数+1=(马驮物的包数-1)×2.
问题2 设牛驮物x包,马驮物y包,你能根据等量关系列出二元一次方程组吗?
问题3 你能算出牛和马各驮物多少包吗?
整理,得
①
②
①-②,得
y=5.
将y=5代入①中,得
x=7.
所以,方程组的解为
答:牛驮物7包,马驮物5包.
归纳总结
列方程解应用题的步骤
1.审题 (找等量关系)
2.设未知数
3.列方程
4.解方程
5.检验,作答
关键:找等量关系、列方程
典例精析
例1 化肥厂往某地区发运了两批化肥,第一批装满了9节火车车厢和25辆卡车,共运走了640t;第二批装满了12节火车车厢和10辆卡车,共运走了760t.平均每节火车车厢和每辆卡车分别装运化肥多少吨?
分析:本题中的等量关系是:
第一批,9节车厢运货吨数+25辆卡车运货吨数=640;
第二批,12节车厢运货吨数+10辆卡车运货吨数=760.
答:平均每节火车车厢装运化肥60t,每辆卡车装运化肥4t.
解:设平均每节火车车厢装运化肥xt,每辆卡车装运化肥yt.
根据题意,得.
3.列
根据题目中的等量关系列出方程组;
解这个方程组,得
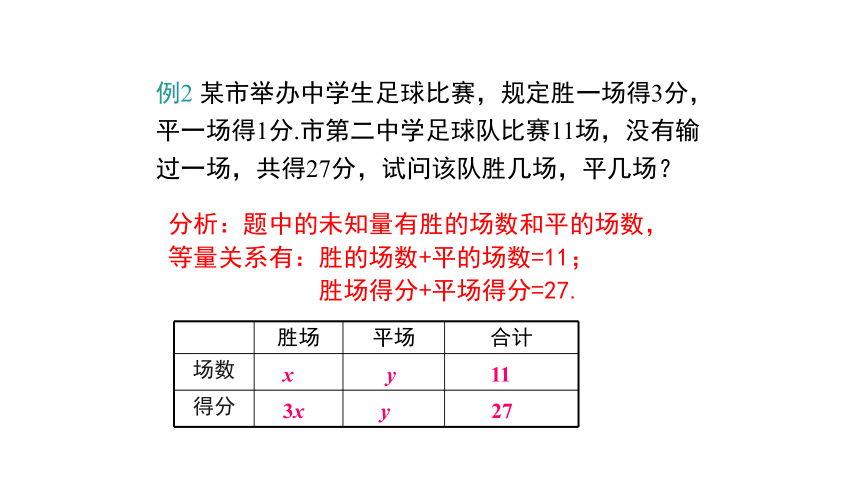
例2 某市举办中学生足球比赛,规定胜一场得3分,平一场得1分.市第二中学足球队比赛11场,没有输过一场,共得27分,试问该队胜几场,平几场?
分析:题中的未知量有胜的场数和平的场数,等量关系有:胜的场数+平的场数=11;
胜场得分+平场得分=27.
胜场
平场
合计
场数
得分
x
3x
y
y
11
27
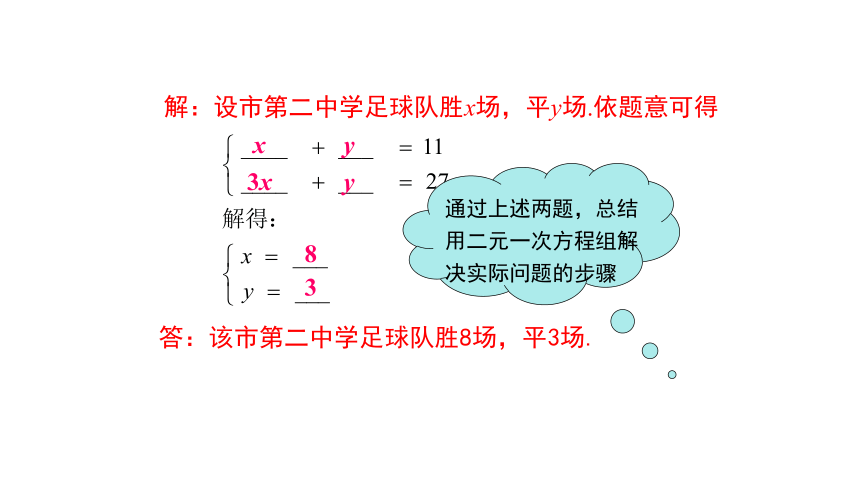
解:设市第二中学足球队胜x场,平y场.依题意可得
8
y
3x
y
3
答:该市第二中学足球队胜8场,平3场.
x
通过上述两题,总结
用二元一次方程组解
决实际问题的步骤
解题小结:用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的_________;
(2)设元:用___________表示题目中的未知数;
(3)列方程组:根据___个等量关系列出方程组;
(4)解方程组:利用__________法或___________解
出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,
然后作答.
总结归纳
数量关系
字母
2
代入消元
加减消元法
例3. 某村18位农民筹集5万元资金,承包了一些低产田地.根据市场调查,他们计划对种植作物的品种进行调整,该种蔬菜和荞麦.种这两种作物每公顷所需的人数和需投入的资金如下表:
作物品种
每公顷所需人数
每公顷投入资金/万元
蔬菜
5
1.5
荞麦
4
1
在现有情况下,这18位农民应承包多少公顷田地,怎样安排终止才能使所有人都有工资,且资金正好够用?
作物品种
种植面积/hm2
需要人数
投入资金/万元
蔬菜
x
5x
1.5x
荞麦
y
4y
y
合计
-----
18
5
将题中出现的量在表格中呈现
解:设蔬菜种植x hm2,荞麦种植y hm2
根据题意可列出方程组:
解方程组,得:
故,承包田地的面积为: x+y=4 hm2
人员安排为为:
5x=5×2=10(人);4y=4×2=8(人)
答:这18位农民应承包4公顷田地,种植蔬菜和荞麦各2公顷,并安排10人种植蔬菜,8人种植荞麦,这样能使所有人都有工作且资金正好够用.
生活中,有很多需要进行配套的问题,如课桌和凳子、螺钉和螺母、电扇叶片和电机等,大家能举出生活中配套问题的例子吗?
列方程组解决配套问题
二
合作探究
某车间有工人660名, 生产甲、乙两种零件.已知每人每天平均生产甲种零件14个或乙种零件20个,1个甲种零件与2个乙种零件为一套.如何调配人员可使每天产的两种零件刚好配套?
问题1 找出本题中的等量关系.
(1) 生产甲种零件的人数+生产乙种零件的人数=660;
(2) 生产的甲种零件的个数×2=生产乙种零件的个数.
问题2 适当设未知数,列出方程组,并解这个方程组.
解:设生产甲种零件的工人有x人, 生产乙种零件的工人有y人.则生产的甲种零件的个数为14x个,生产的乙种零件的个数为20y个.
根据题意,得
解这个方程组,得
答:生产甲种零件的工人有275人, 生产乙种零件的工人有385人.
归纳总结
解决配套问题要弄清:
(1)每套产品中各部分的比例;
(2)生产各部分的工人数之和=工人总数.
例4 某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
分析: 将题中出现的量在表格中呈现
产品类型
所需人数
生产总量
螺钉
x
螺母
y
螺母总产量是螺钉的2倍
人数和为22人
1200x
2000y
解:设生产螺钉的x人,生产螺母的y人.
依题意,可列方程组:
解方程组,得
答:设生产螺钉的10人,生产螺母的12人.
解决配套问题要弄清:
(1)每套产品中各部分的比例;
(2)生产各部分的工人数之和=工人总数.
练一练:北京和上海都有某种仪器可供外地使用,其中北京可提供10台,上海可提供4台.已知重庆需要8台,
武汉需要6台,从北京、上海将仪器运往重庆、武汉
的费用如下表所示.有关部门计划用8000元运送这
些仪器,请你设计一种方案,使武汉、重庆能得到
所需仪器,而且运费正好够用.
运费表
单位:(元
/
台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
解:设从北京运往武汉x台,运往重庆(10-x)台,
设从上海运往武汉y台,运往重庆(4-y)台,
解方程组得
x=4,
y=2.
x+ y=6,
400x+ 300y+800(10-x)+ 500(4-y)=8000.
运费表
单位:(元
/
台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
1. 一块金与银的合金重250g,放在水中称,减轻了 16g. 已知金在水中称,金重减轻 ;银在水中称,银重减轻 . 求这块合金中含金、银各多少克.
解: 设这块合金中含金为x 克,含银为y 克.
根据等量关系得
解这个方程组得
答:这块合金中含金为190克,银60克.
当堂练习
2. 小洪买了80分与60分邮票共17枚,花了12.2元. 试问:80分与60分邮票各买了多少枚?
解:设小洪买80分的邮票共x枚,买60分邮票共y枚,
根据题意有
解得
答:小洪买80分的邮票共10枚,买60分的邮票共7枚.
3.100匹马恰好拉了100片瓦,已知一匹大马能拉3片瓦,3匹小马能拉一片瓦,问有多少匹大马、多少匹小马?
x+y=100
3x+ y=100
解:设有x匹大马, y匹小马,
由题意,得
解此方程组得:
x =25,
y=75.
4. 某星期日,七年级与八年级分别有20,30人去颐和园参观,有30,15人去圆明园参观.七年级买门票花去450元,八年级买门票花去525元.试问:颐和园和圆明园的门票各多少元?
解:设颐和园门票为x元,园明园门票为y元,
根据等量关系得
解这个方程组得
答:颐和园门票为15元,园明园门票为5元.
隔壁听到人分银,
不知人数不知银。
每人五两多六两,
每人六两少五两。
多少人数多少银?
解:设有x个人,y两银,
由题意得:
5x+6=y
6x-5=y
5.古有一捕快,一天晚上他在野外的一个茅屋里,听到外边来了一群人在吵闹,他隐隐约约地听到几个声音,下面有这一古诗为证:
解得:
x=11
y=61
6.王先生家厨房需更换地面瓷砖,他采用两种颜色的砖搭配使用,其中彩色地砖24元/块,单色地砖12元/块,购买的单色地砖数比彩色地砖数的2倍少15块,买两种地砖共花去2220元.求购买的彩色地砖数和单色地砖数.
解:设购买的彩色地砖数为x块,购买的单色地砖数为y块.
根据等量关系得
解这个方程组得
答:购买彩色地砖数为50块,购买单色地砖数为85块.
7. 8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长河宽分别是多少?(单位cm)
60
x+y=60
x=3y
解:设小长方形的长为x, 宽为y,
由题意,得
解此方程组得:
x =45,
y=15.
8.一个工厂共42名工人,每个工人平均每小时生产圆形铁片120片或长方形铁片80片.已知两片圆形铁片与一片长方形铁片可以组成一个圆柱形密封的铁桶.你认为如何安排工人的生产,才能使每天生产的铁片正好配套?
解:设生产圆形铁片的工人x人,生产长方形铁片的工人y人,根据题意列出方程组得
(以下部分由同学们完成)
列方程组解决问题
一般步骤:
审、设、列、解、验、答
课堂小结
关键:找等量关系
讲授新课
当堂练习
课堂小结
6.3 二元一次方程组的应用
第六章 二元一次方程组
第1课时 和差倍分问题、配套问题及行程问题
学习目标
1.能根据具体问题的数量关系,列出二元一次方程组解决和差倍分问题、配套问题及行程问题.(重点、难点)
2.掌握应用二元一次方程组解决实际问题的一般步骤.(重点)
导入新课
情境引入
累死我了!
我还想多给你1包呢!
把我驮的东西给你一包多好哇!这样咱俩驮的包数就一样多了.
那可不行!如果你给我1包,我驮的包数就是你的2倍了.
真的?!
讲授新课
列方程组解决和、差、倍、分问题
一
互动探究
问题1 牛和马的对话中,你能找到哪些等量关系?
(1) 牛驮物的包数-1=马驮物的包数+1;
(2) 牛驮物的包数+1=(马驮物的包数-1)×2.
问题2 设牛驮物x包,马驮物y包,你能根据等量关系列出二元一次方程组吗?
问题3 你能算出牛和马各驮物多少包吗?
整理,得
①
②
①-②,得
y=5.
将y=5代入①中,得
x=7.
所以,方程组的解为
答:牛驮物7包,马驮物5包.
归纳总结
列方程解应用题的步骤
1.审题 (找等量关系)
2.设未知数
3.列方程
4.解方程
5.检验,作答
关键:找等量关系、列方程
典例精析
例1 化肥厂往某地区发运了两批化肥,第一批装满了9节火车车厢和25辆卡车,共运走了640t;第二批装满了12节火车车厢和10辆卡车,共运走了760t.平均每节火车车厢和每辆卡车分别装运化肥多少吨?
分析:本题中的等量关系是:
第一批,9节车厢运货吨数+25辆卡车运货吨数=640;
第二批,12节车厢运货吨数+10辆卡车运货吨数=760.
答:平均每节火车车厢装运化肥60t,每辆卡车装运化肥4t.
解:设平均每节火车车厢装运化肥xt,每辆卡车装运化肥yt.
根据题意,得.
3.列
根据题目中的等量关系列出方程组;
解这个方程组,得
例2 某市举办中学生足球比赛,规定胜一场得3分,平一场得1分.市第二中学足球队比赛11场,没有输过一场,共得27分,试问该队胜几场,平几场?
分析:题中的未知量有胜的场数和平的场数,等量关系有:胜的场数+平的场数=11;
胜场得分+平场得分=27.
胜场
平场
合计
场数
得分
x
3x
y
y
11
27
解:设市第二中学足球队胜x场,平y场.依题意可得
8
y
3x
y
3
答:该市第二中学足球队胜8场,平3场.
x
通过上述两题,总结
用二元一次方程组解
决实际问题的步骤
解题小结:用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的_________;
(2)设元:用___________表示题目中的未知数;
(3)列方程组:根据___个等量关系列出方程组;
(4)解方程组:利用__________法或___________解
出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,
然后作答.
总结归纳
数量关系
字母
2
代入消元
加减消元法
例3. 某村18位农民筹集5万元资金,承包了一些低产田地.根据市场调查,他们计划对种植作物的品种进行调整,该种蔬菜和荞麦.种这两种作物每公顷所需的人数和需投入的资金如下表:
作物品种
每公顷所需人数
每公顷投入资金/万元
蔬菜
5
1.5
荞麦
4
1
在现有情况下,这18位农民应承包多少公顷田地,怎样安排终止才能使所有人都有工资,且资金正好够用?
作物品种
种植面积/hm2
需要人数
投入资金/万元
蔬菜
x
5x
1.5x
荞麦
y
4y
y
合计
-----
18
5
将题中出现的量在表格中呈现
解:设蔬菜种植x hm2,荞麦种植y hm2
根据题意可列出方程组:
解方程组,得:
故,承包田地的面积为: x+y=4 hm2
人员安排为为:
5x=5×2=10(人);4y=4×2=8(人)
答:这18位农民应承包4公顷田地,种植蔬菜和荞麦各2公顷,并安排10人种植蔬菜,8人种植荞麦,这样能使所有人都有工作且资金正好够用.
生活中,有很多需要进行配套的问题,如课桌和凳子、螺钉和螺母、电扇叶片和电机等,大家能举出生活中配套问题的例子吗?
列方程组解决配套问题
二
合作探究
某车间有工人660名, 生产甲、乙两种零件.已知每人每天平均生产甲种零件14个或乙种零件20个,1个甲种零件与2个乙种零件为一套.如何调配人员可使每天产的两种零件刚好配套?
问题1 找出本题中的等量关系.
(1) 生产甲种零件的人数+生产乙种零件的人数=660;
(2) 生产的甲种零件的个数×2=生产乙种零件的个数.
问题2 适当设未知数,列出方程组,并解这个方程组.
解:设生产甲种零件的工人有x人, 生产乙种零件的工人有y人.则生产的甲种零件的个数为14x个,生产的乙种零件的个数为20y个.
根据题意,得
解这个方程组,得
答:生产甲种零件的工人有275人, 生产乙种零件的工人有385人.
归纳总结
解决配套问题要弄清:
(1)每套产品中各部分的比例;
(2)生产各部分的工人数之和=工人总数.
例4 某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
分析: 将题中出现的量在表格中呈现
产品类型
所需人数
生产总量
螺钉
x
螺母
y
螺母总产量是螺钉的2倍
人数和为22人
1200x
2000y
解:设生产螺钉的x人,生产螺母的y人.
依题意,可列方程组:
解方程组,得
答:设生产螺钉的10人,生产螺母的12人.
解决配套问题要弄清:
(1)每套产品中各部分的比例;
(2)生产各部分的工人数之和=工人总数.
练一练:北京和上海都有某种仪器可供外地使用,其中北京可提供10台,上海可提供4台.已知重庆需要8台,
武汉需要6台,从北京、上海将仪器运往重庆、武汉
的费用如下表所示.有关部门计划用8000元运送这
些仪器,请你设计一种方案,使武汉、重庆能得到
所需仪器,而且运费正好够用.
运费表
单位:(元
/
台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
解:设从北京运往武汉x台,运往重庆(10-x)台,
设从上海运往武汉y台,运往重庆(4-y)台,
解方程组得
x=4,
y=2.
x+ y=6,
400x+ 300y+800(10-x)+ 500(4-y)=8000.
运费表
单位:(元
/
台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
1. 一块金与银的合金重250g,放在水中称,减轻了 16g. 已知金在水中称,金重减轻 ;银在水中称,银重减轻 . 求这块合金中含金、银各多少克.
解: 设这块合金中含金为x 克,含银为y 克.
根据等量关系得
解这个方程组得
答:这块合金中含金为190克,银60克.
当堂练习
2. 小洪买了80分与60分邮票共17枚,花了12.2元. 试问:80分与60分邮票各买了多少枚?
解:设小洪买80分的邮票共x枚,买60分邮票共y枚,
根据题意有
解得
答:小洪买80分的邮票共10枚,买60分的邮票共7枚.
3.100匹马恰好拉了100片瓦,已知一匹大马能拉3片瓦,3匹小马能拉一片瓦,问有多少匹大马、多少匹小马?
x+y=100
3x+ y=100
解:设有x匹大马, y匹小马,
由题意,得
解此方程组得:
x =25,
y=75.
4. 某星期日,七年级与八年级分别有20,30人去颐和园参观,有30,15人去圆明园参观.七年级买门票花去450元,八年级买门票花去525元.试问:颐和园和圆明园的门票各多少元?
解:设颐和园门票为x元,园明园门票为y元,
根据等量关系得
解这个方程组得
答:颐和园门票为15元,园明园门票为5元.
隔壁听到人分银,
不知人数不知银。
每人五两多六两,
每人六两少五两。
多少人数多少银?
解:设有x个人,y两银,
由题意得:
5x+6=y
6x-5=y
5.古有一捕快,一天晚上他在野外的一个茅屋里,听到外边来了一群人在吵闹,他隐隐约约地听到几个声音,下面有这一古诗为证:
解得:
x=11
y=61
6.王先生家厨房需更换地面瓷砖,他采用两种颜色的砖搭配使用,其中彩色地砖24元/块,单色地砖12元/块,购买的单色地砖数比彩色地砖数的2倍少15块,买两种地砖共花去2220元.求购买的彩色地砖数和单色地砖数.
解:设购买的彩色地砖数为x块,购买的单色地砖数为y块.
根据等量关系得
解这个方程组得
答:购买彩色地砖数为50块,购买单色地砖数为85块.
7. 8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长河宽分别是多少?(单位cm)
60
x+y=60
x=3y
解:设小长方形的长为x, 宽为y,
由题意,得
解此方程组得:
x =45,
y=15.
8.一个工厂共42名工人,每个工人平均每小时生产圆形铁片120片或长方形铁片80片.已知两片圆形铁片与一片长方形铁片可以组成一个圆柱形密封的铁桶.你认为如何安排工人的生产,才能使每天生产的铁片正好配套?
解:设生产圆形铁片的工人x人,生产长方形铁片的工人y人,根据题意列出方程组得
(以下部分由同学们完成)
列方程组解决问题
一般步骤:
审、设、列、解、验、答
课堂小结
关键:找等量关系
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
