人教版八年级上册数学第十一章三角形章末复习(共26张ppt)
文档属性
| 名称 | 人教版八年级上册数学第十一章三角形章末复习(共26张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 905.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 22:11:32 | ||
图片预览





文档简介
(共26张PPT)
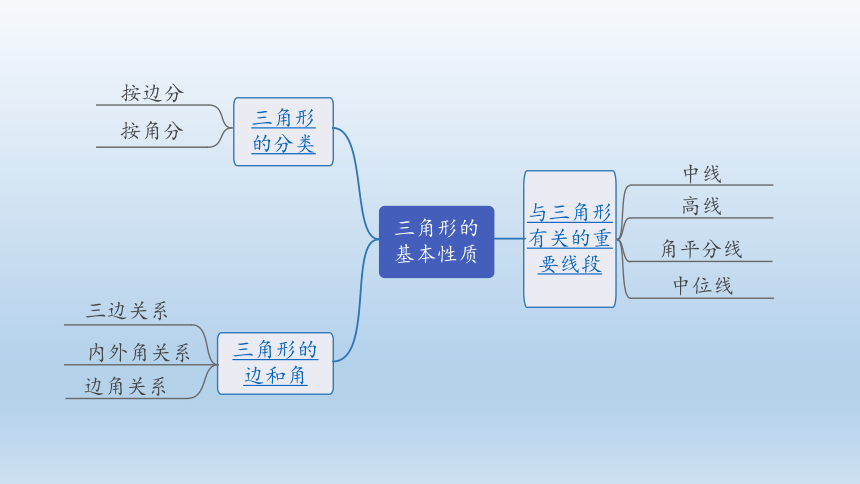
三角形
的分类
三角形的
边和角
与三角形
有关的重
要线段
三角形的
基本性质
按边分
按角分
三边关系
边角关系
内外角关系
中线
高线
角平分线
中位线
【课标要求】
◎探索并证明三角形的内角和定理,掌握它的推论,证明三角形的任意两边之和大于第三边;
◎理解三角形及其内角、外角、中线、高线、角平分线等概念,了解三角形的稳定性;
◎了解三角形的重心的概念;
◎探索并证明三角形的中位线定理.
按边分
1.
三条边都不相等的三角形;
2.
等腰三角形:底边和腰不相等的等腰三角形或等边三角形
按角分
锐角三角形:三个内角都是锐角;
直角三角形:有一个内角是90°;
钝角三角形:有一个内角是钝角
【提分要点】三角形具有稳定性
考点
1
三角形的分类
考点
2
三角形的边和角
三边
关系
三角形任意两边之和________第三边,任意两边之差________第三边;
注:判断给出的三条线段能否组成三角形,只要判断两条较短线段的和是否大于最长线段即可
内外角关系
1.
三角形内角和定理:三角形三个内角的和等于________;
2.
三角形的一个外角等于与它________
的两个内角的_______;
3.
三角形的一个外角大于任何一个与它不相邻的________
边角
关系
在同一个三角形中,等边对等角,等角对等边,大边对大角,小边对小角
大于
小于
180°
不相邻
和
内角
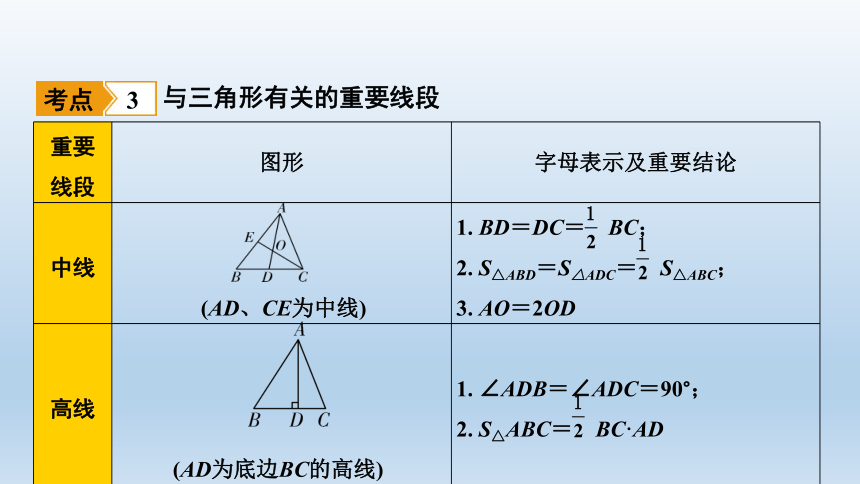
重要
线段
图形
字母表示及重要结论
中线
(AD、CE为中线)
1.
BD=DC=
BC;
2.
S△ABD=S△ADC=
S△ABC;
3.
AO=2OD
高线
(AD为底边BC的高线)
1.
∠ADB=∠ADC=90°;
2.
S△ABC=
BC·AD
考点
3
与三角形有关的重要线段
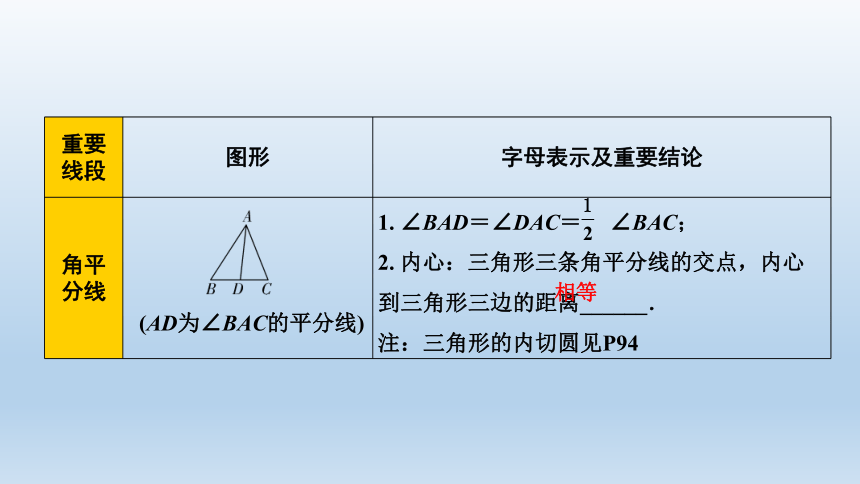
重要
线段
图形
字母表示及重要结论
角平
分线
(AD为∠BAC的平分线)
1.
∠BAD=∠DAC=
∠BAC;
2.
内心:三角形三条角平分线的交点,内心到三角形三边的距离______.
注:三角形的内切圆见P94
相等
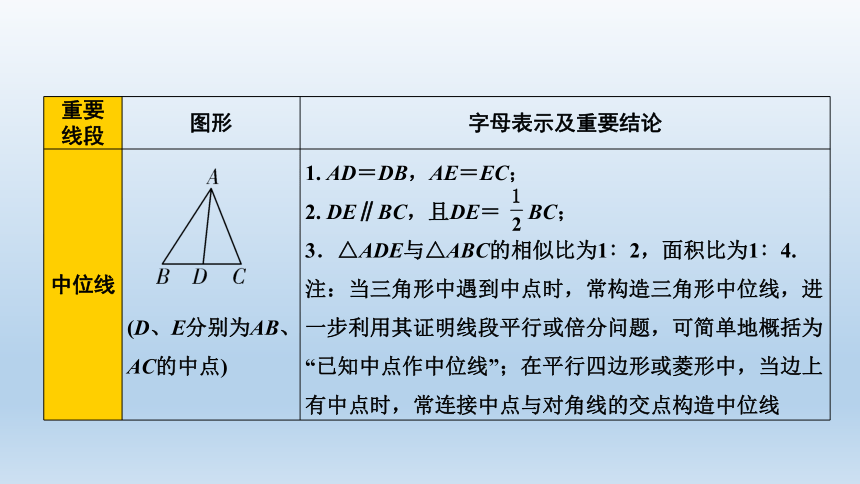
重要
线段
图形
字母表示及重要结论
中位线
(D、E分别为AB、AC的中点)
1.
AD=DB,AE=EC;
2.
DE∥BC,且DE=
BC;
3.△ADE与△ABC的相似比为1∶2,面积比为1∶4.
注:当三角形中遇到中点时,常构造三角形中位线,进一步利用其证明线段平行或倍分问题,可简单地概括为“已知中点作中位线”;在平行四边形或菱形中,当边上有中点时,常连接中点与对角线的交点构造中位线
【知识拓展】中垂线:
1.
DE⊥BC,且BE=CE,BD=CD;
2.
外心:三角形的三条边的中垂线的交点,到三角形三个顶点的距离相等
(DE为线段BC的中垂线)
回归教材
一、证明:三角形的内角和等于180°
1.
证明:“三角形内角和等于180°”这一定理的时候,数学小组的同学们想出来了多种证明方法,A小组代表说,要证三角形内角和等于180°需要凑一个平角,然后利用平角是180°证明三角形内角和是180°;B小组代表说,要证三角形内角和等于180°需要凑两直线平行,利用两直线平行同旁内角互补证明三角形内角和是180°.对于以下三种作图,符合A小组要求的是________,符合B小组要求的是______(填序号).
①③
②
例1题图
二、证明:三角形的中位线平行于第三边,并且等于第三边的一半
2.
(2020河北大模考)在证明定理“三角形的中位线平行于第三边,且等于第三边的一半”时,小明给出如下部分证明过程.
已知:在△ABC中,D、E分别是边AB、AC的中点.
求证:_______________________.
证明:如图,延长DE到点F,使EF=DE,连接CF,
…
(1)补全求证;
(2)请根据添加的辅助线,写出完整的证明过程;
(3)若CE=3,DF=8,求边AB的取值范围.
第2题图
DE∥BC,且DE=
BC
(2)请根据添加的辅助线,写出完整的证明过程;
第2题图
∵点E是AC的中点,∴AE=CE,
又∵EF=ED,∠AED=∠CEF,
∴△ADE≌△CFE.
∴AD=CF,∠A=∠ECF,
∴AD∥CF,∴AB∥CF,
∵点D是AB的中点,∴AD=BD=CF,
∴四边形BDFC是平行四边形,
∴DE∥BC,DF=BC.
∵DE=FE,∴DE=
BC;
(3)若CE=3,DF=8,求边AB的取值范围.
第2题图
∵DF=8,
∴BC=8,
∵CE=3,
∴AC=6.
∴BC-AC即2<AB<14.
一、重要概念、性质定理辨析
练习1 判断下列说法是否正确,对的打“√”,错的打“×”.
(1)两个锐角的和一定大于直角( )
(2)一个锐角的余角一定是一个锐角( )
(3)如果不相等的两个角互补,那么这两个角一个是锐角,一个是钝角( )
(4)一个三角形的外角有1个( )
√
√
×
×
二、与三角形中重要线段有关的计算
例 如图,在△ABC中,点D是BC边上的一点.
(1)如图①,若AD是∠BAC的平分线,
①若∠BAD=40°,则∠BAC=________,DP⊥AC,且DP=2,点D到线段AB的距离为________.
②如图②,若CE是∠ACB的平分线,∠B=30°,则∠AFC=________.
80°
2
105°
例题图
(2)若点D是BC的中点.
①如图③,点E是AB的中点,连接DE.
若∠B=30°,∠C=50°,则∠BED的度数为______;
若AC=4,则DE=________;
②如图③,连接AD,过点A作AF⊥BC于点F.若BC=6,AF=3,则△ABD的面积为______;如图④,过点D作DP∥AB交AC于点P,连接BP,则△ABP的面积为______;
③如图⑤,过点D作GD⊥BC于点D,交AB于点G,连接CG,若AB=6,AC=2,则△AGC的周长为______.
100°
2
8
例题图
(3)如图⑥,∠ACG为△ABC的一个外角,CK平分∠ACG,∠ABC的平分线与CK相交于点K,CD平分∠ACB,交BK于点I,连接AK,设∠BAC=α,∠ABC=β.
①求∠BIC与∠IKC的度数(用含α的式子表示);
②若β=50°,应用①的结论,求∠AKC的度数.
例题图⑥
解:①在△ABC中,∵BI、CI分别平分∠ABC和∠ACB,
∴∠ABC=2∠IBC,∠ACB=2∠ICB,
∵∠BAC+∠ABC+∠ACB=180°,即α+2∠IBC+
2∠ICB=180°①,
在△IBC中,∠BIC+∠IBC+∠ICB=180°②,
2×②-①得2∠BIC-α=180°,即∠BIC=90°+
α,
∵CK平分∠ACG,∴∠ICK=∠ACK+∠ACI=
×180°=90°,
∵∠BIC=∠ICK+∠IKC,
∴∠IKC=∠BIC-∠ICK=90°+
α-90°=α;
例题图⑥
②如解图,连接AI,
由题意知I为△ABC的内心,
∴AI平分∠BAC,
过点K作KO⊥BA交BA延长线于点O,KP⊥AC于点P,KQ⊥BG于点Q,
∵BK平分∠ABC,∴KO=KQ,
又∵CK平分∠ACG,∴KP=KQ,∴KP=KO,
∴AK平分∠CAO,∴∠IAK=90°,
应用①的结论知∠AIC=90°+∠ABC=90°+25°=115°,
在四边形AICK中,∵∠ICK=∠IAK=90°,
∴∠AKC=360°-∠ICK-∠IAK-∠AIC=65°.
例题解图
练习2 (2020抚顺)如图,在△ABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D,若BC=4,则CD的长为________.
练习3 如图,AE是∠BAC的平分线,BD是中线,AE、BD相交于点E,EF⊥AB于F,若AB=14,AC=12,S△BDC=20,则EF的长为________.
2
2
练习2题图
练习3题图
命题点
1
三角形的稳定性(仅2018年考查)
1.
(2018河北1题3分)下列图形具有稳定性的是( )
A
命题点
2
与三角形有关的重要线段(必考,其中2次单独考查)
2.
(2015河北15题2分)如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.
其中会随点P的移动而变化的是( )
A.
②③ B.
②⑤ C.
①③④ D.
④⑤
B
第2题图
3.
(2017河北17题3分)如图,A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200
m,则A,B间的距离为________m.
100
第3题图
三等分角
(2020河南)我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的,人们根据实际需要,发明了一种简易操作工具——三分角器.图①是它的示意图,其中AB与半圆O的直径BC在同一直线上,且AB的长度与半圆的半径相等;DB与AC垂直于点B,DB足够长.
题图
使用方法如图②所示,若要把∠MEN三等分,只需适当放置三分角器,使DB经过∠MEN的顶点E,点A落在边EM上,半圆O与另一边EN恰好相切,切点为F,则EB,EO就把∠MEN三等分了.
为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.
已知:如图②,点A,B,O,C在同一直线上,EB⊥AC,垂足为点B,________.
求证:_________________.
题图
AB=OB
EN切半圆O于点F
解图
证明:如解图,连接OF.
∵EB⊥AC,
∴∠ABE=∠OBE=90°.
又∵AB=OB,EB=EB,
∴△ABE≌△OBE,∴∠1=∠2.
∵EN切半圆O于点F,∴EB=EF.
又∵OB⊥BE且OF=OB,
∴EO平分∠BEF,∴∠3=∠2,
∴∠1=∠2=∠3.
三角形
的分类
三角形的
边和角
与三角形
有关的重
要线段
三角形的
基本性质
按边分
按角分
三边关系
边角关系
内外角关系
中线
高线
角平分线
中位线
【课标要求】
◎探索并证明三角形的内角和定理,掌握它的推论,证明三角形的任意两边之和大于第三边;
◎理解三角形及其内角、外角、中线、高线、角平分线等概念,了解三角形的稳定性;
◎了解三角形的重心的概念;
◎探索并证明三角形的中位线定理.
按边分
1.
三条边都不相等的三角形;
2.
等腰三角形:底边和腰不相等的等腰三角形或等边三角形
按角分
锐角三角形:三个内角都是锐角;
直角三角形:有一个内角是90°;
钝角三角形:有一个内角是钝角
【提分要点】三角形具有稳定性
考点
1
三角形的分类
考点
2
三角形的边和角
三边
关系
三角形任意两边之和________第三边,任意两边之差________第三边;
注:判断给出的三条线段能否组成三角形,只要判断两条较短线段的和是否大于最长线段即可
内外角关系
1.
三角形内角和定理:三角形三个内角的和等于________;
2.
三角形的一个外角等于与它________
的两个内角的_______;
3.
三角形的一个外角大于任何一个与它不相邻的________
边角
关系
在同一个三角形中,等边对等角,等角对等边,大边对大角,小边对小角
大于
小于
180°
不相邻
和
内角
重要
线段
图形
字母表示及重要结论
中线
(AD、CE为中线)
1.
BD=DC=
BC;
2.
S△ABD=S△ADC=
S△ABC;
3.
AO=2OD
高线
(AD为底边BC的高线)
1.
∠ADB=∠ADC=90°;
2.
S△ABC=
BC·AD
考点
3
与三角形有关的重要线段
重要
线段
图形
字母表示及重要结论
角平
分线
(AD为∠BAC的平分线)
1.
∠BAD=∠DAC=
∠BAC;
2.
内心:三角形三条角平分线的交点,内心到三角形三边的距离______.
注:三角形的内切圆见P94
相等
重要
线段
图形
字母表示及重要结论
中位线
(D、E分别为AB、AC的中点)
1.
AD=DB,AE=EC;
2.
DE∥BC,且DE=
BC;
3.△ADE与△ABC的相似比为1∶2,面积比为1∶4.
注:当三角形中遇到中点时,常构造三角形中位线,进一步利用其证明线段平行或倍分问题,可简单地概括为“已知中点作中位线”;在平行四边形或菱形中,当边上有中点时,常连接中点与对角线的交点构造中位线
【知识拓展】中垂线:
1.
DE⊥BC,且BE=CE,BD=CD;
2.
外心:三角形的三条边的中垂线的交点,到三角形三个顶点的距离相等
(DE为线段BC的中垂线)
回归教材
一、证明:三角形的内角和等于180°
1.
证明:“三角形内角和等于180°”这一定理的时候,数学小组的同学们想出来了多种证明方法,A小组代表说,要证三角形内角和等于180°需要凑一个平角,然后利用平角是180°证明三角形内角和是180°;B小组代表说,要证三角形内角和等于180°需要凑两直线平行,利用两直线平行同旁内角互补证明三角形内角和是180°.对于以下三种作图,符合A小组要求的是________,符合B小组要求的是______(填序号).
①③
②
例1题图
二、证明:三角形的中位线平行于第三边,并且等于第三边的一半
2.
(2020河北大模考)在证明定理“三角形的中位线平行于第三边,且等于第三边的一半”时,小明给出如下部分证明过程.
已知:在△ABC中,D、E分别是边AB、AC的中点.
求证:_______________________.
证明:如图,延长DE到点F,使EF=DE,连接CF,
…
(1)补全求证;
(2)请根据添加的辅助线,写出完整的证明过程;
(3)若CE=3,DF=8,求边AB的取值范围.
第2题图
DE∥BC,且DE=
BC
(2)请根据添加的辅助线,写出完整的证明过程;
第2题图
∵点E是AC的中点,∴AE=CE,
又∵EF=ED,∠AED=∠CEF,
∴△ADE≌△CFE.
∴AD=CF,∠A=∠ECF,
∴AD∥CF,∴AB∥CF,
∵点D是AB的中点,∴AD=BD=CF,
∴四边形BDFC是平行四边形,
∴DE∥BC,DF=BC.
∵DE=FE,∴DE=
BC;
(3)若CE=3,DF=8,求边AB的取值范围.
第2题图
∵DF=8,
∴BC=8,
∵CE=3,
∴AC=6.
∴BC-AC
一、重要概念、性质定理辨析
练习1 判断下列说法是否正确,对的打“√”,错的打“×”.
(1)两个锐角的和一定大于直角( )
(2)一个锐角的余角一定是一个锐角( )
(3)如果不相等的两个角互补,那么这两个角一个是锐角,一个是钝角( )
(4)一个三角形的外角有1个( )
√
√
×
×
二、与三角形中重要线段有关的计算
例 如图,在△ABC中,点D是BC边上的一点.
(1)如图①,若AD是∠BAC的平分线,
①若∠BAD=40°,则∠BAC=________,DP⊥AC,且DP=2,点D到线段AB的距离为________.
②如图②,若CE是∠ACB的平分线,∠B=30°,则∠AFC=________.
80°
2
105°
例题图
(2)若点D是BC的中点.
①如图③,点E是AB的中点,连接DE.
若∠B=30°,∠C=50°,则∠BED的度数为______;
若AC=4,则DE=________;
②如图③,连接AD,过点A作AF⊥BC于点F.若BC=6,AF=3,则△ABD的面积为______;如图④,过点D作DP∥AB交AC于点P,连接BP,则△ABP的面积为______;
③如图⑤,过点D作GD⊥BC于点D,交AB于点G,连接CG,若AB=6,AC=2,则△AGC的周长为______.
100°
2
8
例题图
(3)如图⑥,∠ACG为△ABC的一个外角,CK平分∠ACG,∠ABC的平分线与CK相交于点K,CD平分∠ACB,交BK于点I,连接AK,设∠BAC=α,∠ABC=β.
①求∠BIC与∠IKC的度数(用含α的式子表示);
②若β=50°,应用①的结论,求∠AKC的度数.
例题图⑥
解:①在△ABC中,∵BI、CI分别平分∠ABC和∠ACB,
∴∠ABC=2∠IBC,∠ACB=2∠ICB,
∵∠BAC+∠ABC+∠ACB=180°,即α+2∠IBC+
2∠ICB=180°①,
在△IBC中,∠BIC+∠IBC+∠ICB=180°②,
2×②-①得2∠BIC-α=180°,即∠BIC=90°+
α,
∵CK平分∠ACG,∴∠ICK=∠ACK+∠ACI=
×180°=90°,
∵∠BIC=∠ICK+∠IKC,
∴∠IKC=∠BIC-∠ICK=90°+
α-90°=α;
例题图⑥
②如解图,连接AI,
由题意知I为△ABC的内心,
∴AI平分∠BAC,
过点K作KO⊥BA交BA延长线于点O,KP⊥AC于点P,KQ⊥BG于点Q,
∵BK平分∠ABC,∴KO=KQ,
又∵CK平分∠ACG,∴KP=KQ,∴KP=KO,
∴AK平分∠CAO,∴∠IAK=90°,
应用①的结论知∠AIC=90°+∠ABC=90°+25°=115°,
在四边形AICK中,∵∠ICK=∠IAK=90°,
∴∠AKC=360°-∠ICK-∠IAK-∠AIC=65°.
例题解图
练习2 (2020抚顺)如图,在△ABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D,若BC=4,则CD的长为________.
练习3 如图,AE是∠BAC的平分线,BD是中线,AE、BD相交于点E,EF⊥AB于F,若AB=14,AC=12,S△BDC=20,则EF的长为________.
2
2
练习2题图
练习3题图
命题点
1
三角形的稳定性(仅2018年考查)
1.
(2018河北1题3分)下列图形具有稳定性的是( )
A
命题点
2
与三角形有关的重要线段(必考,其中2次单独考查)
2.
(2015河北15题2分)如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.
其中会随点P的移动而变化的是( )
A.
②③ B.
②⑤ C.
①③④ D.
④⑤
B
第2题图
3.
(2017河北17题3分)如图,A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200
m,则A,B间的距离为________m.
100
第3题图
三等分角
(2020河南)我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的,人们根据实际需要,发明了一种简易操作工具——三分角器.图①是它的示意图,其中AB与半圆O的直径BC在同一直线上,且AB的长度与半圆的半径相等;DB与AC垂直于点B,DB足够长.
题图
使用方法如图②所示,若要把∠MEN三等分,只需适当放置三分角器,使DB经过∠MEN的顶点E,点A落在边EM上,半圆O与另一边EN恰好相切,切点为F,则EB,EO就把∠MEN三等分了.
为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.
已知:如图②,点A,B,O,C在同一直线上,EB⊥AC,垂足为点B,________.
求证:_________________.
题图
AB=OB
EN切半圆O于点F
解图
证明:如解图,连接OF.
∵EB⊥AC,
∴∠ABE=∠OBE=90°.
又∵AB=OB,EB=EB,
∴△ABE≌△OBE,∴∠1=∠2.
∵EN切半圆O于点F,∴EB=EF.
又∵OB⊥BE且OF=OB,
∴EO平分∠BEF,∴∠3=∠2,
∴∠1=∠2=∠3.
