7.5三角形的内角和(2)-苏科版七年级数学下册课件(共21张PPT)
文档属性
| 名称 | 7.5三角形的内角和(2)-苏科版七年级数学下册课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 241.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 00:00:00 | ||
图片预览




文档简介
( 苏科版.七年级数学 下册 )
7.5 三角形的内角和(2)
教学目标
1探索并了解四边形及一般多边形内角和公式。
2能运用多边形内角和的结论,进行角的计算和说理。
了解一下
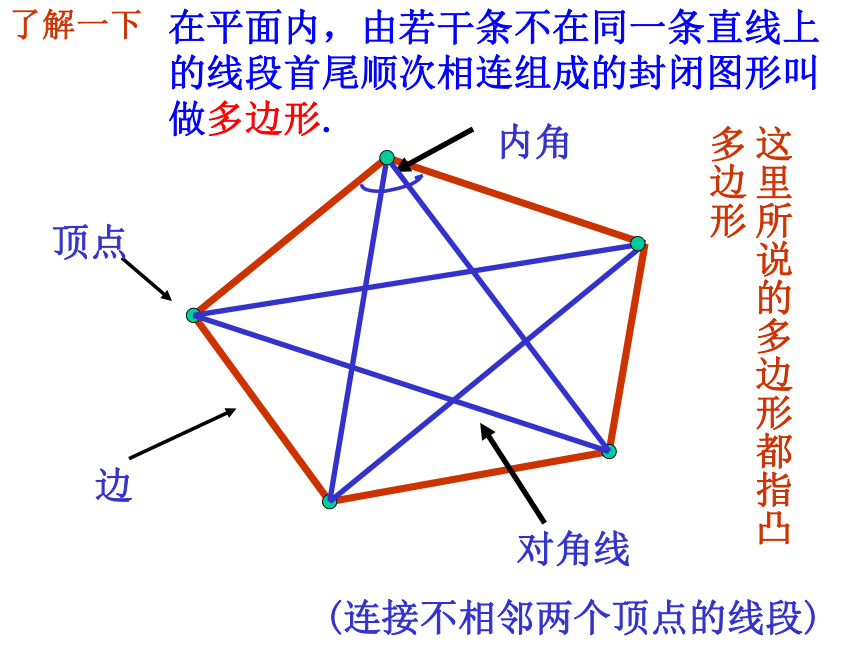
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形.
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
这里所说的多边形都指凸多边形
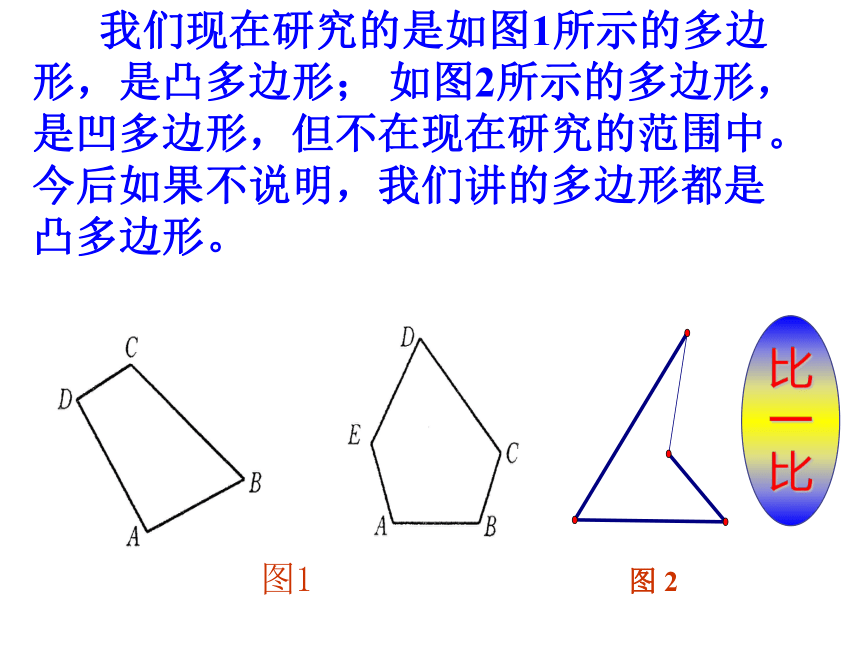
我们现在研究的是如图1所示的多边形,是凸多边形; 如图2所示的多边形,是凹多边形,但不在现在研究的范围中。今后如果不说明,我们讲的多边形都是凸多边形。
图 2
比
一
比
图1
三角形3个内角之间的关系
三角形3个内角的和等于180°.
知识回顾
D
A
B
C
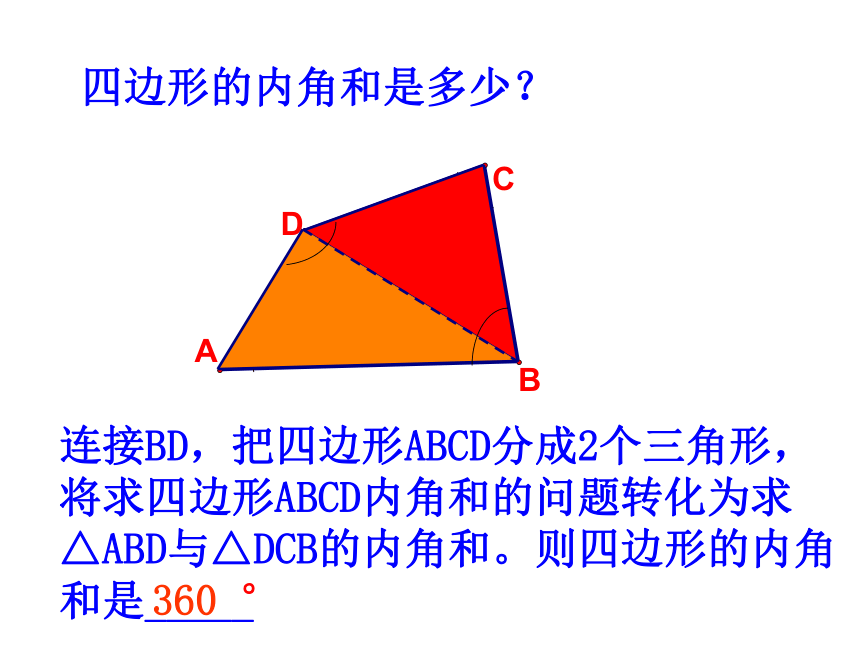
连接BD,把四边形ABCD分成2个三角形,将求四边形ABCD内角和的问题转化为求△ABD与△DCB的内角和。则四边形的内角和是_____
四边形的内角和是多少?
360 °
E
A
B
C
D
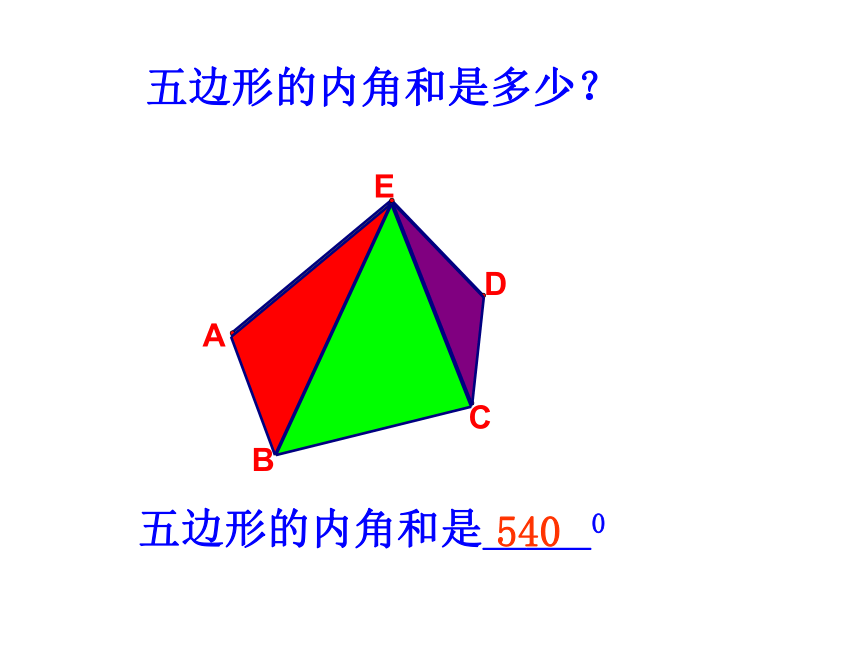
五边形的内角和是多少?
五边形的内角和是_____0
540
F
A
B
C
D
E
六边形的内角和是多少?
六边形的内角和是_____0
720
D
A
B
C
E
A
B
C
D
F
A
B
C
D
E
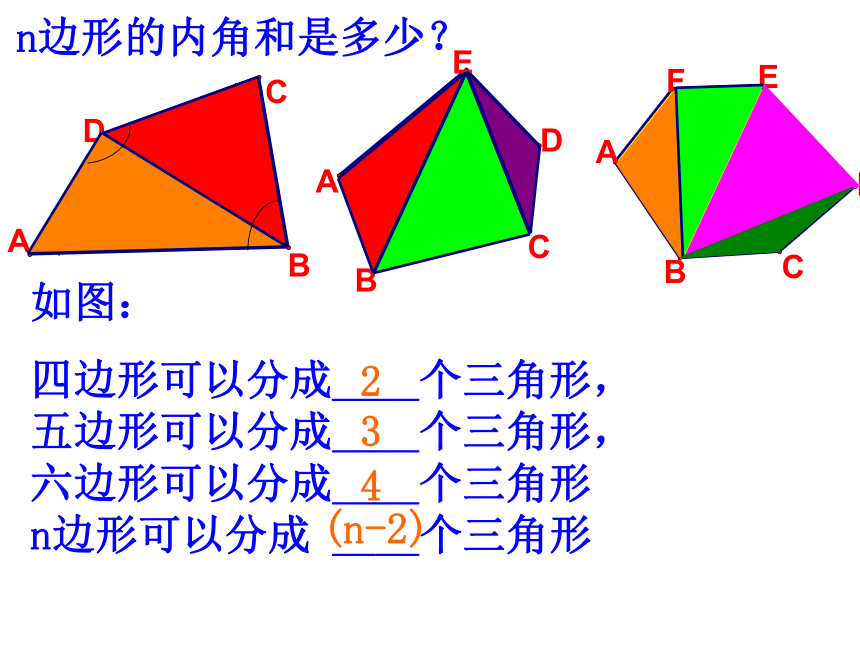
n边形的内角和是多少?
如图:
四边形可以分成____个三角形, 五边形可以分成____个三角形, 六边形可以分成____个三角形 n边形可以分成 ____个三角形
2
3
4
(n-2)
D
A
B
C
E
A
B
C
D
F
A
B
C
D
E
多边形的边数
3
4
5
6
7
…
n
分成三角形的个数
1
2
3
…
多边形的内角和
1800
1800×2
1800×3
…
4
5
n-2
180°×4
180°×5
180°×(n-2)
由此我们得出了:
n边形的内角和等于(n-2) ·1800
你还有其他的方法计算多边形的内角和吗?
D
A
B
C
四边形还可以这样分:
那么四边形的内角和可以表示为:
4×1800-3600
五边形还可以这样分:
那么五边形的内角和可以表示为:
5×1800-3600
E
A
B
C
D
六边形还可以这样分:
那么六边形的内角和可以表示为:
6×1800-3600
F
A
B
C
D
E
多边形的边数
4
5
6
7
…
n
分成三角形的个数
4
5
…
多边形的内角和
4×1800-3600=
(4-2)×1800
5×1800-3600=
(5-2)×1800
…
D
A
B
C
E
A
B
C
D
F
A
B
C
D
E
6×1800
-3600=
(6-2)×1800
7×1800
-3600=
(7-2)×1800
n×1800
-3600=
(n-2)×1800
6
7
n
例题讲解:
一个多边形的内角和为1080°,这个多边形是几边形?
解:设这个多边形为n边形,由题意可得:
180×(n-2)=1080
解得 : n=8
答:这个多边形为8边形.
例题讲解:
求八边形的内角和的度数。
解:(n-2)×180°
=(8-2)×180°
= 1080°
答:八边形的内角和为1080°。
练一练:
2、如果一个多边形的内角和是1440度,那么这个多边形是几边形?
解:由多边形的内角和公式可得
(n - 2)· 1800 = 14400
(n - 2) = 8
n = 10
∴这是十边形。
练一练:
3、若n边形的每一个内角是144度,
那么n= .
解:由多边形的内角和公式可得:
(n - 2) · 180 = 144n
180n – 360 = 144n
180n -144n=360
36n = 360
n = 10
10
巩固练习:
2、多边形内角和为1080°则它是
( )边形。
3、多边形内角和为1800°则它是
( )边形。
4、两个多边形的边数之比为1:2,
内角和之比为1:4,求两个多边
形的边数。
1、十边形内角和为( )
课堂小结
请用一句话总结:
这节课我收获的知识是
我学到的一种思想方法是
课堂作业:
课本P34-35习题7.5第7,8题.
7.5 三角形的内角和(2)
教学目标
1探索并了解四边形及一般多边形内角和公式。
2能运用多边形内角和的结论,进行角的计算和说理。
了解一下
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形.
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
这里所说的多边形都指凸多边形
我们现在研究的是如图1所示的多边形,是凸多边形; 如图2所示的多边形,是凹多边形,但不在现在研究的范围中。今后如果不说明,我们讲的多边形都是凸多边形。
图 2
比
一
比
图1
三角形3个内角之间的关系
三角形3个内角的和等于180°.
知识回顾
D
A
B
C
连接BD,把四边形ABCD分成2个三角形,将求四边形ABCD内角和的问题转化为求△ABD与△DCB的内角和。则四边形的内角和是_____
四边形的内角和是多少?
360 °
E
A
B
C
D
五边形的内角和是多少?
五边形的内角和是_____0
540
F
A
B
C
D
E
六边形的内角和是多少?
六边形的内角和是_____0
720
D
A
B
C
E
A
B
C
D
F
A
B
C
D
E
n边形的内角和是多少?
如图:
四边形可以分成____个三角形, 五边形可以分成____个三角形, 六边形可以分成____个三角形 n边形可以分成 ____个三角形
2
3
4
(n-2)
D
A
B
C
E
A
B
C
D
F
A
B
C
D
E
多边形的边数
3
4
5
6
7
…
n
分成三角形的个数
1
2
3
…
多边形的内角和
1800
1800×2
1800×3
…
4
5
n-2
180°×4
180°×5
180°×(n-2)
由此我们得出了:
n边形的内角和等于(n-2) ·1800
你还有其他的方法计算多边形的内角和吗?
D
A
B
C
四边形还可以这样分:
那么四边形的内角和可以表示为:
4×1800-3600
五边形还可以这样分:
那么五边形的内角和可以表示为:
5×1800-3600
E
A
B
C
D
六边形还可以这样分:
那么六边形的内角和可以表示为:
6×1800-3600
F
A
B
C
D
E
多边形的边数
4
5
6
7
…
n
分成三角形的个数
4
5
…
多边形的内角和
4×1800-3600=
(4-2)×1800
5×1800-3600=
(5-2)×1800
…
D
A
B
C
E
A
B
C
D
F
A
B
C
D
E
6×1800
-3600=
(6-2)×1800
7×1800
-3600=
(7-2)×1800
n×1800
-3600=
(n-2)×1800
6
7
n
例题讲解:
一个多边形的内角和为1080°,这个多边形是几边形?
解:设这个多边形为n边形,由题意可得:
180×(n-2)=1080
解得 : n=8
答:这个多边形为8边形.
例题讲解:
求八边形的内角和的度数。
解:(n-2)×180°
=(8-2)×180°
= 1080°
答:八边形的内角和为1080°。
练一练:
2、如果一个多边形的内角和是1440度,那么这个多边形是几边形?
解:由多边形的内角和公式可得
(n - 2)· 1800 = 14400
(n - 2) = 8
n = 10
∴这是十边形。
练一练:
3、若n边形的每一个内角是144度,
那么n= .
解:由多边形的内角和公式可得:
(n - 2) · 180 = 144n
180n – 360 = 144n
180n -144n=360
36n = 360
n = 10
10
巩固练习:
2、多边形内角和为1080°则它是
( )边形。
3、多边形内角和为1800°则它是
( )边形。
4、两个多边形的边数之比为1:2,
内角和之比为1:4,求两个多边
形的边数。
1、十边形内角和为( )
课堂小结
请用一句话总结:
这节课我收获的知识是
我学到的一种思想方法是
课堂作业:
课本P34-35习题7.5第7,8题.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
