苏科版七年级数学下7.1《探索直线平行的条件(2)》课件(共23张PPT)
文档属性
| 名称 | 苏科版七年级数学下7.1《探索直线平行的条件(2)》课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 21:36:45 | ||
图片预览



文档简介
2020
7.1探索直线平行的条件(第二课时)
苏教版七年级下册 数学
复习回顾
1
如图:在“三线八角”中,
1
3
7
5
2
4
8
6
D
C
A
B
E
F
你能找出哪些具有特殊位置关系的角?
其中∠3与∠4 角。
同位
4
“三线八角”中
同位角有 对。
若∠3=∠4,则直线AB与CD有何位置关系呢?
复习回顾:
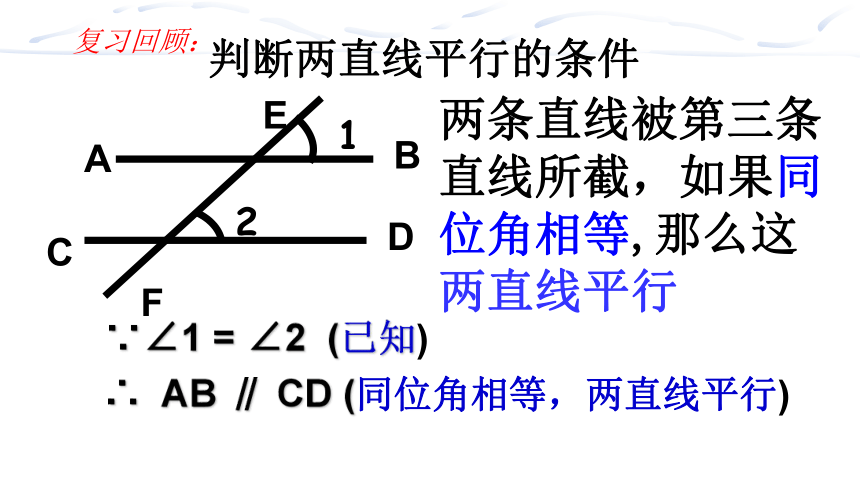
判断两直线平行的条件
两条直线被第三条直线所截,如果同位角相等,那么这两直线平行
E
B
A
C
D
F
1
2
∵∠1 = ∠2 (已知)
∴ AB ∥ CD (同位角相等,两直线平行)
复习回顾:
探索新知
2
内错角像个什么字母呢?
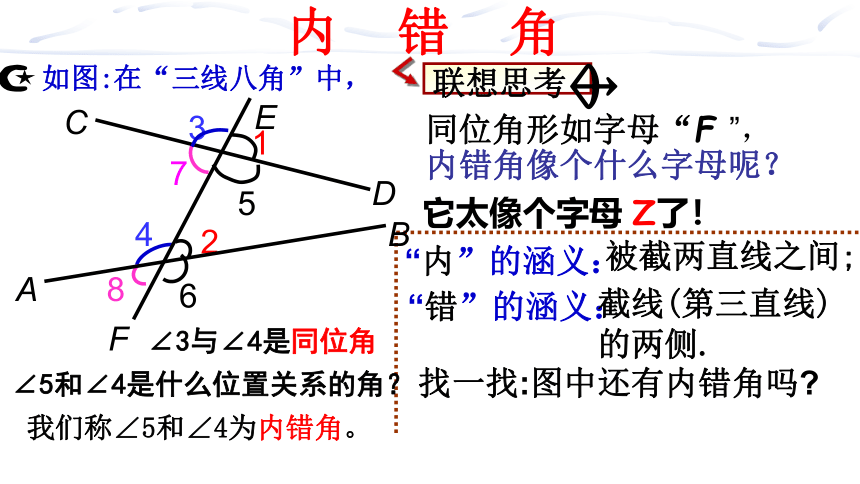
我们称∠5和∠4为内错角。
?
联想思考
同位角形如字母“F ”,
它太像个字母 Z了!
内 错 角
“内”的涵义:
被截两直线之间;
“错”的涵义:
截线(第三直线)的两侧.
找一找:图中还有内错角吗?
如图:在“三线八角”中,
1
3
7
5
2
4
8
6
D
C
A
B
E
F
∠3与∠4是同位角
∠5和∠4是什么位置关系的角?
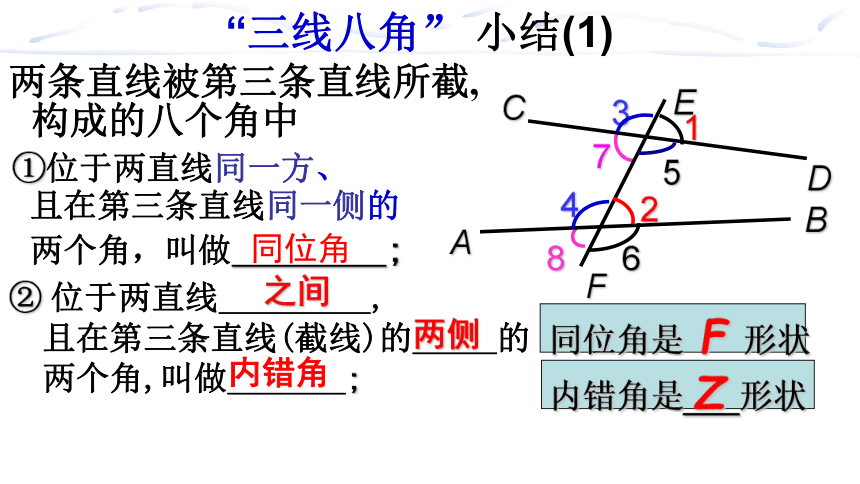
“三线八角” 小结(1)
F
1
3
7
5
2
8
6
D
C
A
B
E
4
构成的八个角中
两条直线被第三条直线所截,
①位于两直线同一方、
② 位于两直线 ,
且在第三条直线(截线)的 的
两个角,叫做_______;
且在第三条直线同一侧的
两个角,叫做 ;
同位角
之间
两侧
同位角是 F 形状
内错角是 形状
Z
内错角
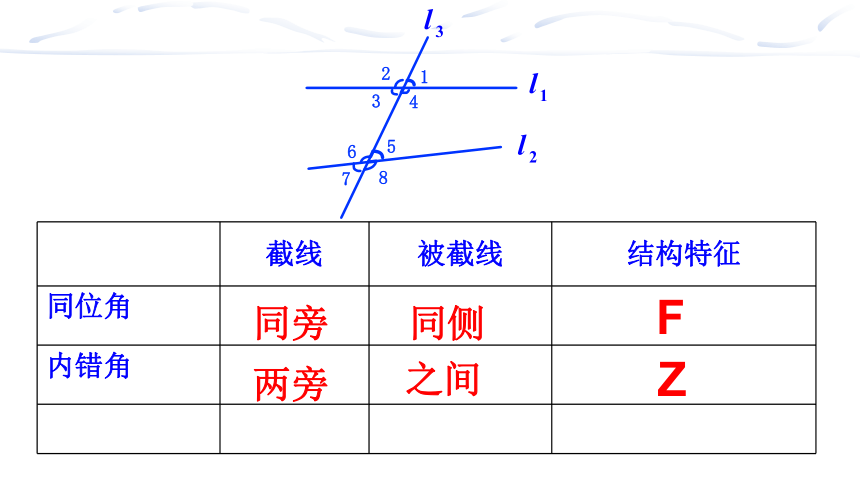
截线
被截线
结构特征
同位角
内错角
之间
同侧
两旁
同旁
F
Z
A
B
C
D
E
1
3
2
4
5
6
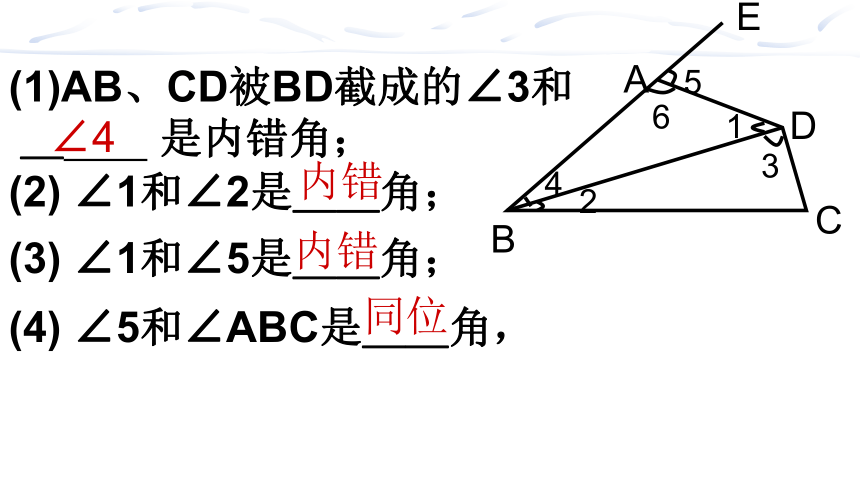
(1)AB、CD被BD截成的∠3和
_ 是内错角;
∠4
(2) ∠1和∠2是__角;
(4) ∠5和∠ABC是__角,
内错
同位
(3) ∠1和∠5是__角;
内错
下图中,如果∠1=∠2,
能得出a∥b吗?
思考
a
1
b
2
c
1
b
a
c
2
证明:
∵ ∠1 = ∠3
( )
对顶角相等
∠1= ∠2 ( )
已知
∴ ∠2 = ∠3 ( )
∴ 直线 a∥b ( ).
等量代换
同位角相等,两直线平行
?
证明思路
两直线平行
同位角相等
对顶角相等
内错角相等
议一议
3
如果∠1=∠2,能得出a∥b吗?
两直线平行的条件:
两条直线被第三条直线所截,
如果内错角相等,那么这两直线平行.
B
1
2
A
D
E
F
C
∵ ∠1=∠2 (已知)
∴ AB//CD
(内错角相等,两直线平行)
两直线平行的判定条件
同位角相等,两直线平行.
内错角相等,两直线平行.
例题讲解
3
例1、如图,∠1=∠2,∠B+∠BDE=180°。
(1)图中哪些直线互相平行,为什么?
(2)∠2与哪个角相等时,DE∥BC?∠A与哪个角相等时,AB∥EF?
答:(1) ①∵ ∠1=∠2(已知)
1
2
A
B
C
E
D
F
∴AB ∥ EF(内错角相等,两直线平行)
② ∵∠B+∠BDE=180°(已知)
∠1+∠BDE=180 ° ( 平角的定义)
∴ ∠B=∠1(同角的补角相等)
∴DE ∥ BC(同位角相等,两直线平行)
(2) 当∠2=∠EFC时, DE∥BC
当∠A=∠FEC时, AB∥EF
∵BE平分∠ABD,(已知)
∴ ∠DBE= ∠ABE(角平分线的定义)
∵ ∠DBE=∠A(已知)
∴ ∠ABE=∠A(等量代换)
∴BE ∥ AC(内错角相等,两直线平行)
答:BE ∥ AC
例2:点B在DC上,BE平分∠ABD,∠DBE=∠A,你能判断BE与AC的位置关系吗?请说明理由。
×
×
例3:已知∠3=45 °,∠1与∠2互余,试说明AB//CD
解:∵∠1与∠2 互余 ,(已知)
1
2
3
A
B
C
D
∵ ∠3=45°(已知)
∴ AB∥CD(内错角相等,两直线平行)
∵∠1=∠2(对顶角相等)
∴∠2=45°(等式的性质)
∴∠ 2=∠3(等量代换)
∴2∠2=90°(等量代换)
∴∠1+∠2=90°(余角的定义)
例4 如图,BC、DE分别平分?ABD和?BDF,且?1=?2,请找出平行线,并说明理由。
解⑴∵BC、DE分别平分?ABD和?BDF(已知)
∴?1=∠3 ;?2= ?4(角平分线的定义)
∵∠1=∠2(已知)
∴?3=∠4(等量代换)
∴BC∥DE
(内错角相等,两直线平行)
答:(1)BC∥DE (2)AB∥DF
2
3
A
B
D
F
C
E
1
4
例4 如图,BC、DE分别平分?ABD和?BDF,且?1=?2,请找出平行线,并说明理由。
2
1
A
B
D
F
C
E
解⑵ ∵BC、DE分别平分?ABD和?BDF(已知)
∴?ABD=2∠1
?BDF=2∠2(角平分线的定义)
∵∠1=∠2(已知)
∴?ABD=∠BDF(等量代换)
∴AB∥DF
(内错角相等,两直线平行)
(2)AB∥DF
两直线平行的判定条件
同位角相等,两直线平行.
内错角相等,两直线平行.
同位角是 F 形状
内错角是 形状
Z
自主练习
4
7.1探索直线平行的条件(第二课时)
苏教版七年级下册 数学
复习回顾
1
如图:在“三线八角”中,
1
3
7
5
2
4
8
6
D
C
A
B
E
F
你能找出哪些具有特殊位置关系的角?
其中∠3与∠4 角。
同位
4
“三线八角”中
同位角有 对。
若∠3=∠4,则直线AB与CD有何位置关系呢?
复习回顾:
判断两直线平行的条件
两条直线被第三条直线所截,如果同位角相等,那么这两直线平行
E
B
A
C
D
F
1
2
∵∠1 = ∠2 (已知)
∴ AB ∥ CD (同位角相等,两直线平行)
复习回顾:
探索新知
2
内错角像个什么字母呢?
我们称∠5和∠4为内错角。
?
联想思考
同位角形如字母“F ”,
它太像个字母 Z了!
内 错 角
“内”的涵义:
被截两直线之间;
“错”的涵义:
截线(第三直线)的两侧.
找一找:图中还有内错角吗?
如图:在“三线八角”中,
1
3
7
5
2
4
8
6
D
C
A
B
E
F
∠3与∠4是同位角
∠5和∠4是什么位置关系的角?
“三线八角” 小结(1)
F
1
3
7
5
2
8
6
D
C
A
B
E
4
构成的八个角中
两条直线被第三条直线所截,
①位于两直线同一方、
② 位于两直线 ,
且在第三条直线(截线)的 的
两个角,叫做_______;
且在第三条直线同一侧的
两个角,叫做 ;
同位角
之间
两侧
同位角是 F 形状
内错角是 形状
Z
内错角
截线
被截线
结构特征
同位角
内错角
之间
同侧
两旁
同旁
F
Z
A
B
C
D
E
1
3
2
4
5
6
(1)AB、CD被BD截成的∠3和
_ 是内错角;
∠4
(2) ∠1和∠2是__角;
(4) ∠5和∠ABC是__角,
内错
同位
(3) ∠1和∠5是__角;
内错
下图中,如果∠1=∠2,
能得出a∥b吗?
思考
a
1
b
2
c
1
b
a
c
2
证明:
∵ ∠1 = ∠3
( )
对顶角相等
∠1= ∠2 ( )
已知
∴ ∠2 = ∠3 ( )
∴ 直线 a∥b ( ).
等量代换
同位角相等,两直线平行
?
证明思路
两直线平行
同位角相等
对顶角相等
内错角相等
议一议
3
如果∠1=∠2,能得出a∥b吗?
两直线平行的条件:
两条直线被第三条直线所截,
如果内错角相等,那么这两直线平行.
B
1
2
A
D
E
F
C
∵ ∠1=∠2 (已知)
∴ AB//CD
(内错角相等,两直线平行)
两直线平行的判定条件
同位角相等,两直线平行.
内错角相等,两直线平行.
例题讲解
3
例1、如图,∠1=∠2,∠B+∠BDE=180°。
(1)图中哪些直线互相平行,为什么?
(2)∠2与哪个角相等时,DE∥BC?∠A与哪个角相等时,AB∥EF?
答:(1) ①∵ ∠1=∠2(已知)
1
2
A
B
C
E
D
F
∴AB ∥ EF(内错角相等,两直线平行)
② ∵∠B+∠BDE=180°(已知)
∠1+∠BDE=180 ° ( 平角的定义)
∴ ∠B=∠1(同角的补角相等)
∴DE ∥ BC(同位角相等,两直线平行)
(2) 当∠2=∠EFC时, DE∥BC
当∠A=∠FEC时, AB∥EF
∵BE平分∠ABD,(已知)
∴ ∠DBE= ∠ABE(角平分线的定义)
∵ ∠DBE=∠A(已知)
∴ ∠ABE=∠A(等量代换)
∴BE ∥ AC(内错角相等,两直线平行)
答:BE ∥ AC
例2:点B在DC上,BE平分∠ABD,∠DBE=∠A,你能判断BE与AC的位置关系吗?请说明理由。
×
×
例3:已知∠3=45 °,∠1与∠2互余,试说明AB//CD
解:∵∠1与∠2 互余 ,(已知)
1
2
3
A
B
C
D
∵ ∠3=45°(已知)
∴ AB∥CD(内错角相等,两直线平行)
∵∠1=∠2(对顶角相等)
∴∠2=45°(等式的性质)
∴∠ 2=∠3(等量代换)
∴2∠2=90°(等量代换)
∴∠1+∠2=90°(余角的定义)
例4 如图,BC、DE分别平分?ABD和?BDF,且?1=?2,请找出平行线,并说明理由。
解⑴∵BC、DE分别平分?ABD和?BDF(已知)
∴?1=∠3 ;?2= ?4(角平分线的定义)
∵∠1=∠2(已知)
∴?3=∠4(等量代换)
∴BC∥DE
(内错角相等,两直线平行)
答:(1)BC∥DE (2)AB∥DF
2
3
A
B
D
F
C
E
1
4
例4 如图,BC、DE分别平分?ABD和?BDF,且?1=?2,请找出平行线,并说明理由。
2
1
A
B
D
F
C
E
解⑵ ∵BC、DE分别平分?ABD和?BDF(已知)
∴?ABD=2∠1
?BDF=2∠2(角平分线的定义)
∵∠1=∠2(已知)
∴?ABD=∠BDF(等量代换)
∴AB∥DF
(内错角相等,两直线平行)
(2)AB∥DF
两直线平行的判定条件
同位角相等,两直线平行.
内错角相等,两直线平行.
同位角是 F 形状
内错角是 形状
Z
自主练习
4
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
