苏科版七年级数学下册 7.5多边形的内角和与外角和课件 20张ppt
文档属性
| 名称 | 苏科版七年级数学下册 7.5多边形的内角和与外角和课件 20张ppt |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 00:00:00 | ||
图片预览


文档简介
7.5 多边形的内角和与外角和
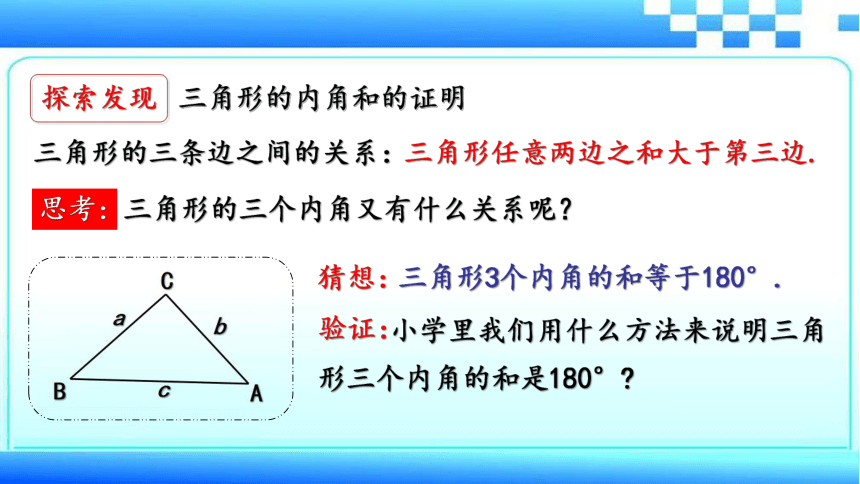
三角形的三条边之间的关系:
三角形任意两边之和大于第三边.
三角形的三个内角又有什么关系呢?
探索发现
思考:
猜想:
三角形3个内角的和等于180°.
小学里我们用什么方法来说明三角形三个内角的和是180°?
验证:
三角形的内角和的证明
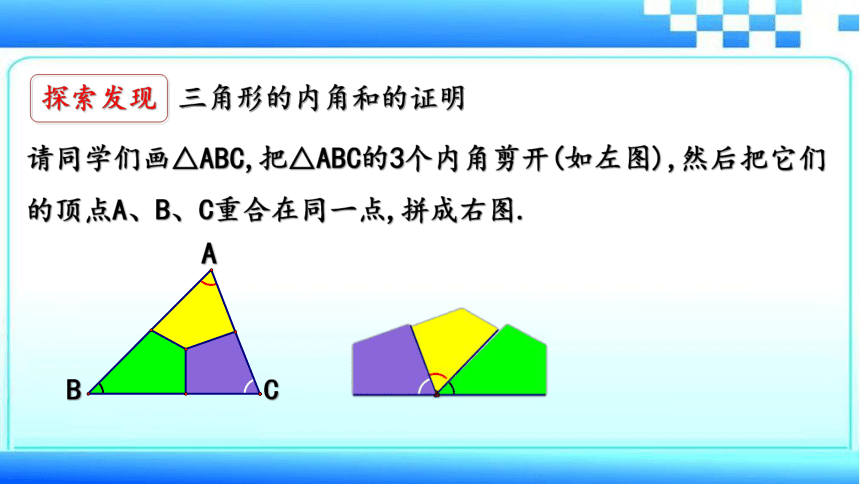
探索发现
三角形的内角和的证明
请同学们画△ABC,把△ABC的3个内角剪开(如左图),然后把它们的顶点A、B、C重合在同一点,拼成右图.
A
B
C
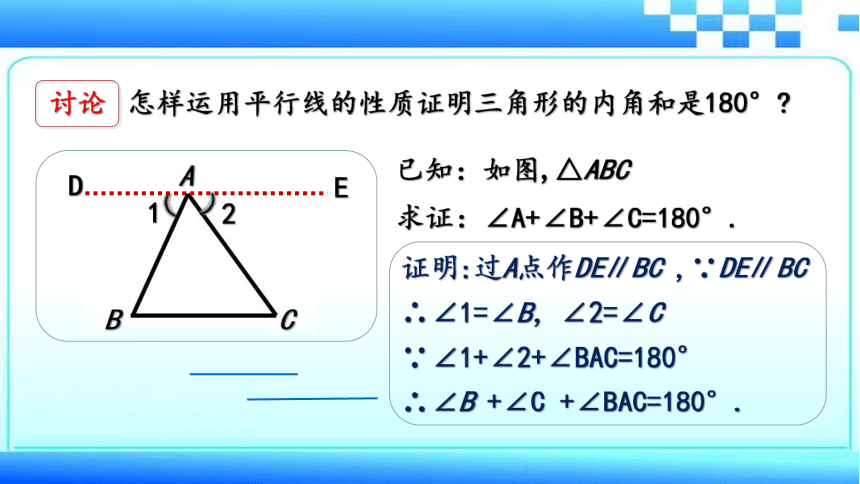
讨论
怎样运用平行线的性质证明三角形的内角和是180°?
D
E
1
2
已知:如图,△ABC
求证:∠A+∠B+∠C=180°.
证明:过A点作DE∥BC ,∵DE∥BC
∴∠1=∠B,∠2=∠C
∵∠1+∠2+∠BAC=180°
∴∠B +∠C +∠BAC=180°.
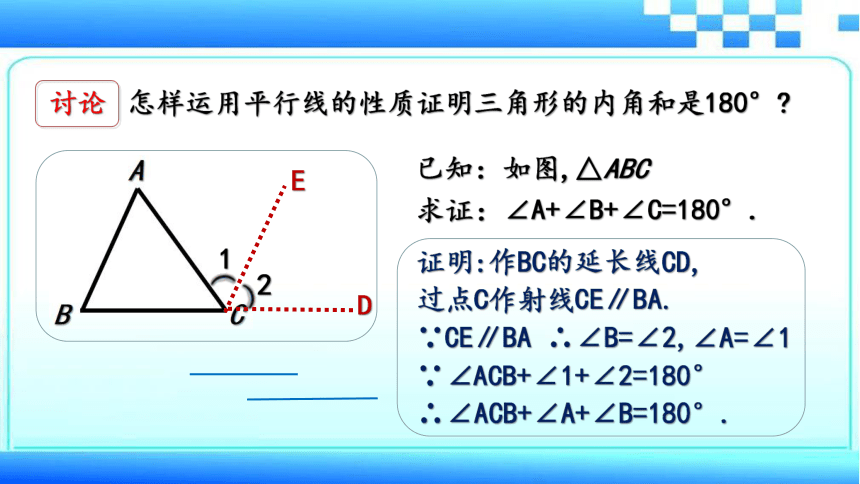
讨论
怎样运用平行线的性质证明三角形的内角和是180°?
已知:如图,△ABC
求证:∠A+∠B+∠C=180°.
证明:作BC的延长线CD,
过点C作射线CE∥BA.
∵CE∥BA ∴∠B=∠2,∠A=∠1
∵∠ACB+∠1+∠2=180°
∴∠ACB+∠A+∠B=180°.
E
D
1
2
反馈练习:
1.在直角三角形中,∠C是直角,则∠A与∠B的和是多少?
结论:
直角三角形的两个锐角互余.
2.在三角形ABC中,∠A=40°,∠B=∠C.求∠C的度数.
∵∠A+∠B+∠C=180°,∠B=∠C.∴∠C=(180°-∠A )÷2=70°
3.∠A:∠B:∠C=2:3:4,则∠A=__;∠B=__;∠C=__.
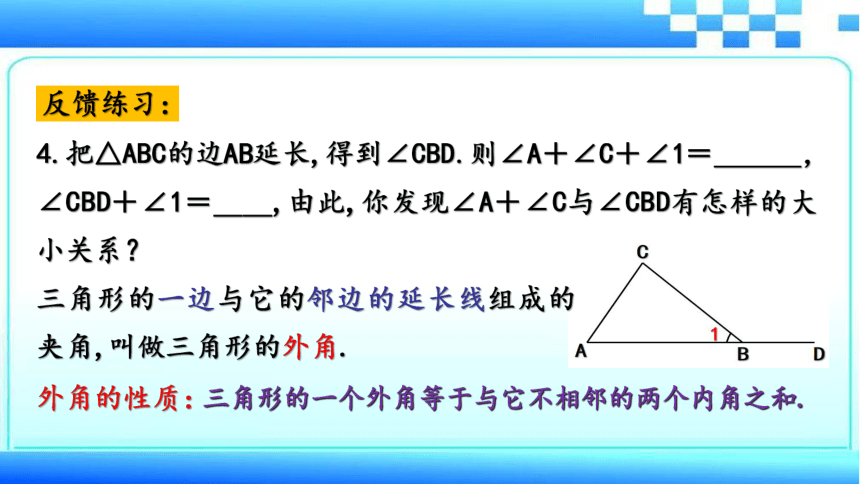
4.把△ABC的边AB延长,得到∠CBD.则∠A+∠C+∠1=___,∠CBD+∠1=__,由此,你发现∠A+∠C与∠CBD有怎样的大小关系?
反馈练习:
三角形的一边与它的邻边的延长线组成的夹角,叫做三角形的外角.
外角的性质:
三角形的一个外角等于与它不相邻的两个内角之和.
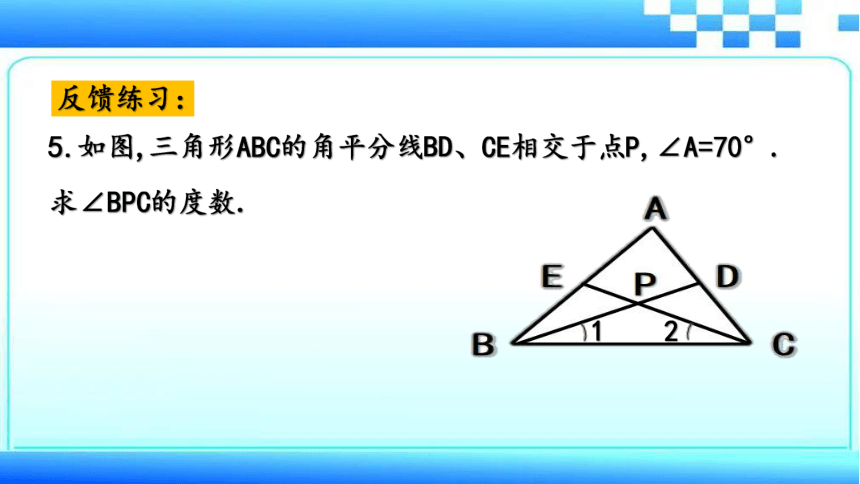
5.如图,三角形ABC的角平分线BD、CE相交于点P,∠A=70°.
求∠BPC的度数.
反馈练习:
2
1
反馈练习:
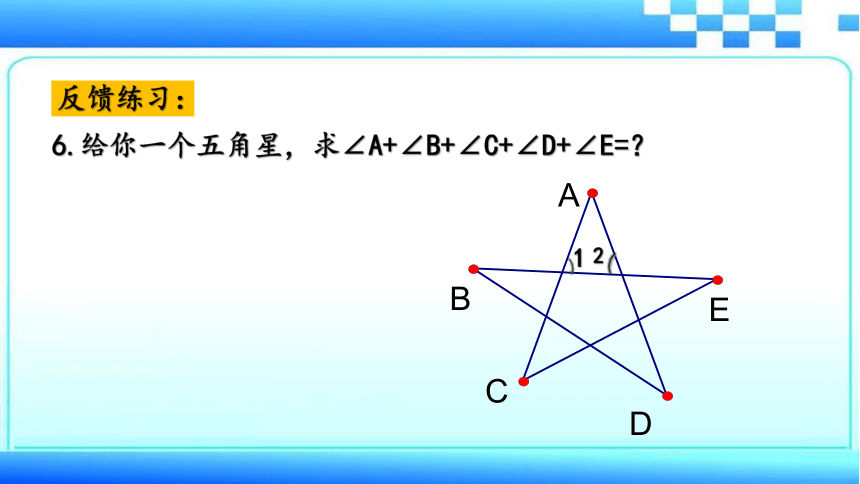
6.给你一个五角星,求∠A+∠B+∠C+∠D+∠E=?
2
1
反馈练习:
7.如图,AC、BD相交于点O,∠A+∠B=∠C+∠D吗?为什么?
B
A
O
C
D
解:∠A+∠B=∠C+∠D
∵在△AOB中∠A+∠B+∠AOB=180°
∴∠A+∠B=180°-∠AOB
在△COD中∠C+∠D+∠COD=180°
∴∠C+∠D=180°-∠COD
∵∠AOB与∠COD是对顶角
∴∠AOB=∠COD
∴∠A+∠B=∠C+∠D
(等量代换)
在图中,四边形ABCD、五边形ABCDE的内角和分别等于多少度?(提示:把四边形、五边形分成几个三角形)
议一议
A
B
C
D
类似地,n边形可以分成多少个三角形?它的内角和是多少度?
4-2
5-2
6-2
n-2
180°
180°
180°
180°
×2
×3
×4
×(n-2)
n边形内角和等于(n-2)×180°.
多边形外角介绍:
n边形一共有多少个外角?
2n个
多边形每个顶点处的两个外角有何关系?
在多边形的每个顶点处取一个外角,将它们的和叫做多边形的外角和.
想一想
多边形的外角和有相应的规律吗?
多边形外角和:
正三角形的每一个内角是______.
每一个外角是_______.
则正三角形的外角和是_______.
60°
120°
360°
正方形的每一个内角是_______.
90°
每一个外角是________.
90°
则正方形的外角和是_______.
360°
多边形外角和:
正五边形的每一个内角是_______.
108°
每一个外角是_______.
72°
则五边形的外角和是_______.
360°
多边形外角和:
120°×3=360°
90°×4=360°
72°×5=360°
你能推出正n边形的外角和也是360°吗?
多边形外角和:
一般的多边形的外角和也是360°吗?
探究:
数学实验室
我们已经知道n边形的内角和等于(n-2)×180°,根据这个结论,你能求出n边形的外角和吗?
提示:n边形的每个内角与它们相邻的外角互补,它们的总和为n×180°.
由此我们知道:多边形的外角和等于360°.
反馈练习:
8.已知一个正多边形的每一个外角等于60°,则这个正多边形是( )
A.正五边形 B.正六边形
C.正七边形 D.正八边形
作业:完成课时作业本相应习题.
要求:字迹工整,表述科学.
三角形的三条边之间的关系:
三角形任意两边之和大于第三边.
三角形的三个内角又有什么关系呢?
探索发现
思考:
猜想:
三角形3个内角的和等于180°.
小学里我们用什么方法来说明三角形三个内角的和是180°?
验证:
三角形的内角和的证明
探索发现
三角形的内角和的证明
请同学们画△ABC,把△ABC的3个内角剪开(如左图),然后把它们的顶点A、B、C重合在同一点,拼成右图.
A
B
C
讨论
怎样运用平行线的性质证明三角形的内角和是180°?
D
E
1
2
已知:如图,△ABC
求证:∠A+∠B+∠C=180°.
证明:过A点作DE∥BC ,∵DE∥BC
∴∠1=∠B,∠2=∠C
∵∠1+∠2+∠BAC=180°
∴∠B +∠C +∠BAC=180°.
讨论
怎样运用平行线的性质证明三角形的内角和是180°?
已知:如图,△ABC
求证:∠A+∠B+∠C=180°.
证明:作BC的延长线CD,
过点C作射线CE∥BA.
∵CE∥BA ∴∠B=∠2,∠A=∠1
∵∠ACB+∠1+∠2=180°
∴∠ACB+∠A+∠B=180°.
E
D
1
2
反馈练习:
1.在直角三角形中,∠C是直角,则∠A与∠B的和是多少?
结论:
直角三角形的两个锐角互余.
2.在三角形ABC中,∠A=40°,∠B=∠C.求∠C的度数.
∵∠A+∠B+∠C=180°,∠B=∠C.∴∠C=(180°-∠A )÷2=70°
3.∠A:∠B:∠C=2:3:4,则∠A=__;∠B=__;∠C=__.
4.把△ABC的边AB延长,得到∠CBD.则∠A+∠C+∠1=___,∠CBD+∠1=__,由此,你发现∠A+∠C与∠CBD有怎样的大小关系?
反馈练习:
三角形的一边与它的邻边的延长线组成的夹角,叫做三角形的外角.
外角的性质:
三角形的一个外角等于与它不相邻的两个内角之和.
5.如图,三角形ABC的角平分线BD、CE相交于点P,∠A=70°.
求∠BPC的度数.
反馈练习:
2
1
反馈练习:
6.给你一个五角星,求∠A+∠B+∠C+∠D+∠E=?
2
1
反馈练习:
7.如图,AC、BD相交于点O,∠A+∠B=∠C+∠D吗?为什么?
B
A
O
C
D
解:∠A+∠B=∠C+∠D
∵在△AOB中∠A+∠B+∠AOB=180°
∴∠A+∠B=180°-∠AOB
在△COD中∠C+∠D+∠COD=180°
∴∠C+∠D=180°-∠COD
∵∠AOB与∠COD是对顶角
∴∠AOB=∠COD
∴∠A+∠B=∠C+∠D
(等量代换)
在图中,四边形ABCD、五边形ABCDE的内角和分别等于多少度?(提示:把四边形、五边形分成几个三角形)
议一议
A
B
C
D
类似地,n边形可以分成多少个三角形?它的内角和是多少度?
4-2
5-2
6-2
n-2
180°
180°
180°
180°
×2
×3
×4
×(n-2)
n边形内角和等于(n-2)×180°.
多边形外角介绍:
n边形一共有多少个外角?
2n个
多边形每个顶点处的两个外角有何关系?
在多边形的每个顶点处取一个外角,将它们的和叫做多边形的外角和.
想一想
多边形的外角和有相应的规律吗?
多边形外角和:
正三角形的每一个内角是______.
每一个外角是_______.
则正三角形的外角和是_______.
60°
120°
360°
正方形的每一个内角是_______.
90°
每一个外角是________.
90°
则正方形的外角和是_______.
360°
多边形外角和:
正五边形的每一个内角是_______.
108°
每一个外角是_______.
72°
则五边形的外角和是_______.
360°
多边形外角和:
120°×3=360°
90°×4=360°
72°×5=360°
你能推出正n边形的外角和也是360°吗?
多边形外角和:
一般的多边形的外角和也是360°吗?
探究:
数学实验室
我们已经知道n边形的内角和等于(n-2)×180°,根据这个结论,你能求出n边形的外角和吗?
提示:n边形的每个内角与它们相邻的外角互补,它们的总和为n×180°.
由此我们知道:多边形的外角和等于360°.
反馈练习:
8.已知一个正多边形的每一个外角等于60°,则这个正多边形是( )
A.正五边形 B.正六边形
C.正七边形 D.正八边形
作业:完成课时作业本相应习题.
要求:字迹工整,表述科学.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
