苏科版七年级数学下册 9.3 多项式乘多项式 课件 (24张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 9.3 多项式乘多项式 课件 (24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 533.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 21:40:24 | ||
图片预览





文档简介
9.3 多项式乘多项式
七年级(下册)
初中数学
即将迈入个位数主播的十一线主播
林大大
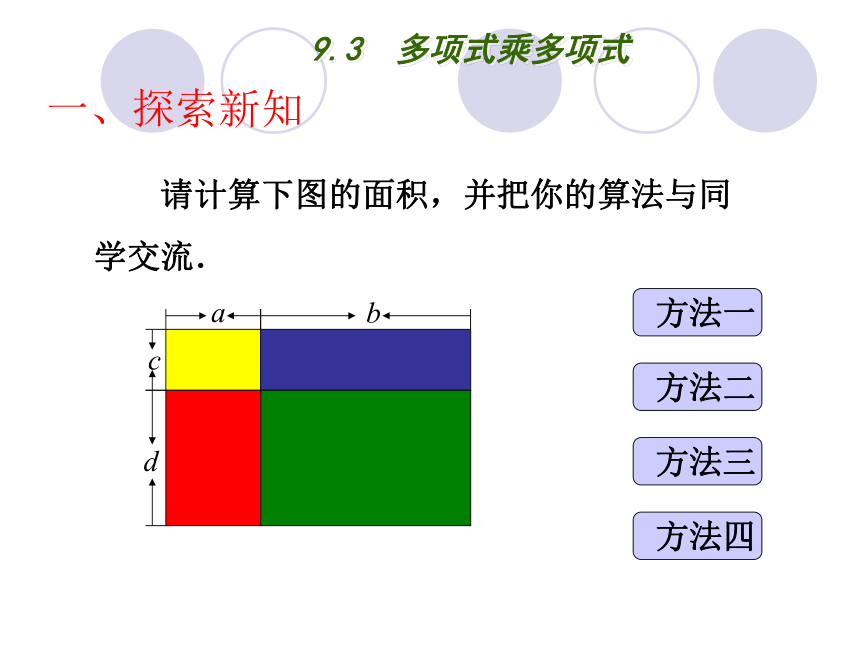
请计算下图的面积,并把你的算法与同学交流.
9.3 多项式乘多项式
方法一
方法二
方法三
方法四
一、探索新知
9.3 多项式乘多项式
如果把此图看成是一个长为 ,宽为 的长方形.
则此图的面积为:
9.3 多项式乘多项式
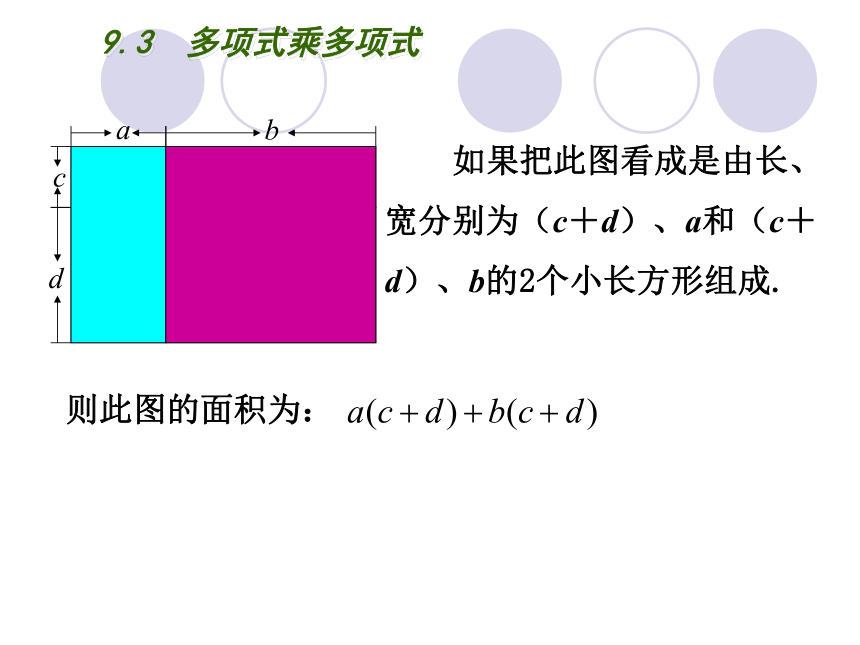
如果把此图看成是由长、宽分别为(c+d)、a和(c+d)、b的2个小长方形组成.
则此图的面积为:
如果把此图看成是由长、宽分别为(a+b)、c和(a+b)、d的2个小长方形组成,
9.3 多项式乘多项式
则此图的面积为:
9.3 多项式乘多项式
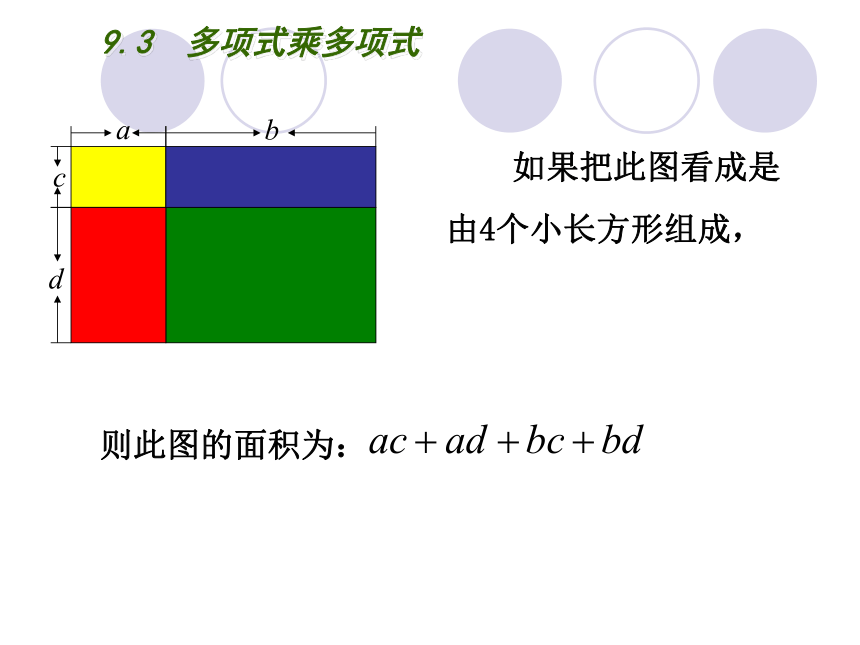
如果把此图看成是由4个小长方形组成,
则此图的面积为:
9.3 多项式乘多项式
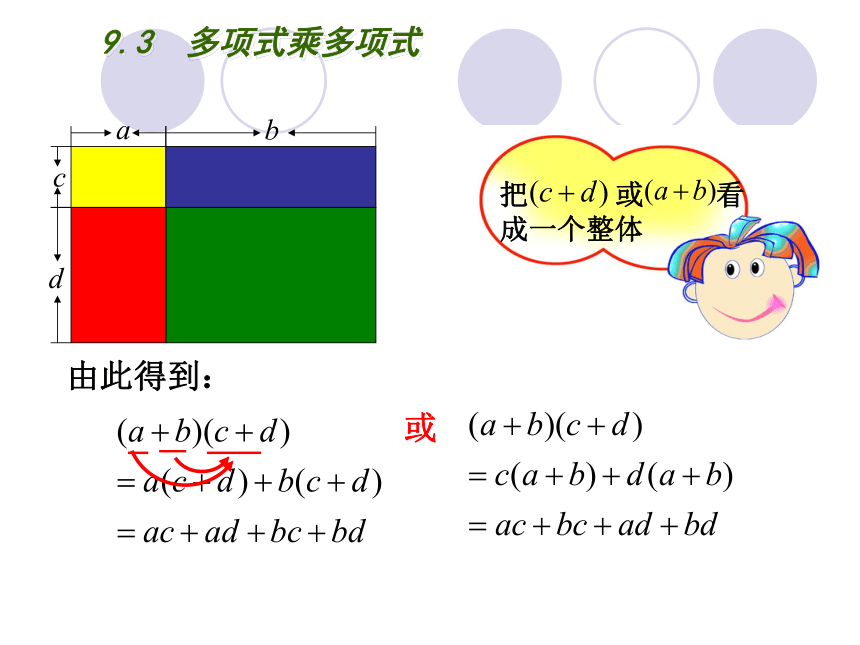
由此得到:
把 或 看
成一个整体
或
9.3 多项式乘多项式
上面的运算过程,也可以表示为
多项式乘多项式的运算法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
二、归纳总结
注意:多项式与多项式相乘的结果中,要把同类项合并.
如何计算下列各式,请说明理由.
(1)(a+4)(a+3)
(2)(3x+1)(x-2)
(1)解=a·a+a·3+4·a+12
=a·a+3a+4a+12
=a2+7a+12
(2)解:=3x·x+3x·(-2)+x+(-2)
=3x2-6x+x-2
=3x2-5x-2
例1 计算:
(1) (2)
(3) (4)
三、典型例题
【练习1】
(1)计算:n(n+2)(2n+1)= .
(2)中间偶数为2n的三个连续偶数的积是 .
(3)给出下列四个等式:
① (a-2b)(3a+b)=3a2-5ab-2b2
② (2x+1)(2x-1)=4x2-x-1
③ (x+y)(x-y)=x2-xy-y2
④ (m+2)(3m+6)=3m2+6m+12
其中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
判别下列解法是否正确,若错请说出理由。
解:原式
例2:
判别下列解法是否正确,若错请说出理由。
解:原式
判别下列解法是否正确,若错请说出理由。
解:原式
1、漏乘
需要注意的几个问题
2、符号问题
3、最后结果应化成最简形式
【练习2】
如图,阴影部分的面积是 .
【例3】先化简,再求值:
(a-3b)2+(3a+b)(3a-b),其中a=-1,b=1.
(x+2)(x-3)
解:=x·x+x·(-3)+2·x-6
=x2-3x+2x-6
=x2-x-6
(x-2)(x-3)
解:=x·x+x·(-3)+x·(-2)+6
=x2-3x-2x+6
=x2-5x+6
一般地,(x+a)(x+b)=x2+ax+bx+ab =x2+(a+b)x+ab(a,b为已知数)
x的一次项的系数是什么?如何得来的?
计算的结果会不会出现只有两项的情况?
1.若(x-a)(x+b)=x2+Mx+N,则M、N分别为( )
A.M=b-a,N=-ab
B.M=b-a,N=ab
C.M=a-b,N=-ab
D.M=a+b,N=-ab
2.若x2+mx-15=(x+3)(x+n),则mn= .
【练习3】
1.解方程:(x+6)(x-5)-(x-1)(x+5)=24
2.当m为何值时,(x2-3x+4)(x3+x+m)的展开式中不含x的一次项?
知识拓展
通过今天的学习,你学到了什么?说出来大家分享.
9.3 多项式乘多项式
多项式乘多项式
单项式乘多项式
单项式乘单项式
转化
转化
9.3 多项式乘多项式
【课后作业】
1.课本习题9.3第2,3题,过程清晰完整;
2.PPT最后一页,必须抄题目,做在习题9.3下面;
注:以上作业请及时发到小组群里,不要老是需要催.
3.本周末第二次自我检测,星期天下午四点之前必须QQ私发给我,五点公布答案自行订正.
5.若 ,则m=___,n=____ .
6.若 ,则(a+1)(b-1)=_____.
四、巩固训练
计算:
(1)
(2)
(3)
(4)
2.先化简,再求值:
(3a+1)(2a-3)-(6a-5)(a-4),其中a=-0.5.
3.如果(x+2)(x2-ax+1)的乘积中不含x2项,那么a= .
4.若 的乘积中不含x2与x3的项,求p、q的值.
七年级(下册)
初中数学
即将迈入个位数主播的十一线主播
林大大
请计算下图的面积,并把你的算法与同学交流.
9.3 多项式乘多项式
方法一
方法二
方法三
方法四
一、探索新知
9.3 多项式乘多项式
如果把此图看成是一个长为 ,宽为 的长方形.
则此图的面积为:
9.3 多项式乘多项式
如果把此图看成是由长、宽分别为(c+d)、a和(c+d)、b的2个小长方形组成.
则此图的面积为:
如果把此图看成是由长、宽分别为(a+b)、c和(a+b)、d的2个小长方形组成,
9.3 多项式乘多项式
则此图的面积为:
9.3 多项式乘多项式
如果把此图看成是由4个小长方形组成,
则此图的面积为:
9.3 多项式乘多项式
由此得到:
把 或 看
成一个整体
或
9.3 多项式乘多项式
上面的运算过程,也可以表示为
多项式乘多项式的运算法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
二、归纳总结
注意:多项式与多项式相乘的结果中,要把同类项合并.
如何计算下列各式,请说明理由.
(1)(a+4)(a+3)
(2)(3x+1)(x-2)
(1)解=a·a+a·3+4·a+12
=a·a+3a+4a+12
=a2+7a+12
(2)解:=3x·x+3x·(-2)+x+(-2)
=3x2-6x+x-2
=3x2-5x-2
例1 计算:
(1) (2)
(3) (4)
三、典型例题
【练习1】
(1)计算:n(n+2)(2n+1)= .
(2)中间偶数为2n的三个连续偶数的积是 .
(3)给出下列四个等式:
① (a-2b)(3a+b)=3a2-5ab-2b2
② (2x+1)(2x-1)=4x2-x-1
③ (x+y)(x-y)=x2-xy-y2
④ (m+2)(3m+6)=3m2+6m+12
其中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
判别下列解法是否正确,若错请说出理由。
解:原式
例2:
判别下列解法是否正确,若错请说出理由。
解:原式
判别下列解法是否正确,若错请说出理由。
解:原式
1、漏乘
需要注意的几个问题
2、符号问题
3、最后结果应化成最简形式
【练习2】
如图,阴影部分的面积是 .
【例3】先化简,再求值:
(a-3b)2+(3a+b)(3a-b),其中a=-1,b=1.
(x+2)(x-3)
解:=x·x+x·(-3)+2·x-6
=x2-3x+2x-6
=x2-x-6
(x-2)(x-3)
解:=x·x+x·(-3)+x·(-2)+6
=x2-3x-2x+6
=x2-5x+6
一般地,(x+a)(x+b)=x2+ax+bx+ab =x2+(a+b)x+ab(a,b为已知数)
x的一次项的系数是什么?如何得来的?
计算的结果会不会出现只有两项的情况?
1.若(x-a)(x+b)=x2+Mx+N,则M、N分别为( )
A.M=b-a,N=-ab
B.M=b-a,N=ab
C.M=a-b,N=-ab
D.M=a+b,N=-ab
2.若x2+mx-15=(x+3)(x+n),则mn= .
【练习3】
1.解方程:(x+6)(x-5)-(x-1)(x+5)=24
2.当m为何值时,(x2-3x+4)(x3+x+m)的展开式中不含x的一次项?
知识拓展
通过今天的学习,你学到了什么?说出来大家分享.
9.3 多项式乘多项式
多项式乘多项式
单项式乘多项式
单项式乘单项式
转化
转化
9.3 多项式乘多项式
【课后作业】
1.课本习题9.3第2,3题,过程清晰完整;
2.PPT最后一页,必须抄题目,做在习题9.3下面;
注:以上作业请及时发到小组群里,不要老是需要催.
3.本周末第二次自我检测,星期天下午四点之前必须QQ私发给我,五点公布答案自行订正.
5.若 ,则m=___,n=____ .
6.若 ,则(a+1)(b-1)=_____.
四、巩固训练
计算:
(1)
(2)
(3)
(4)
2.先化简,再求值:
(3a+1)(2a-3)-(6a-5)(a-4),其中a=-0.5.
3.如果(x+2)(x2-ax+1)的乘积中不含x2项,那么a= .
4.若 的乘积中不含x2与x3的项,求p、q的值.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
