苏科版七年级数学下册 7.2:探索平行线的性质 课件 (19张ppt)
文档属性
| 名称 | 苏科版七年级数学下册 7.2:探索平行线的性质 课件 (19张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 21:41:14 | ||
图片预览






文档简介
7.2 探索平行线的性质
复习与回顾
(1)∵∠1=∠___,∴a∥b( )
(2)∵∠ =∠2,∴a∥b( )
3
2
同位角相等,两直线平行
内错角相等,两直线平行
根据下图回答下列问题.
(3)∵∠ +∠2= .∴a∥b( )
4
180°
同旁内角互补,两直线平行
1.同位角相等; 2.内错角相等; 3.同旁内角互补
判定条件
如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
思考:
1.在练习本上画两条平行线AB、CD,再画直线EF与直线AB、CD相交.指出图中的同位角、内错角、同旁内角.
数学实验室
2.把图剪成如图所示的四块纸片,分别把图中的每对同位角叠合,你发现了什么?
结论:
图中每对同位角都相等.
由此,我们知道:两条平行直线被第三条直线所截,同位角都相等.
简单说成:两直线平行,同位角相等.
做一做
分别把图中每对内错角叠合,你发现了什么?
把图中的每对同旁内角拼在一起,它们之间有怎样的数量关系?
结论:
图中每对内错角都相等;每对同旁内角都互补.
例1:如图:已知a//b,那么?2与?3相等吗?为什么?
解:∵a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
b
1
2
a
c
3
合作交流
结论:
两条平行线被第三条直线所截,内错角相等.
解:∵a//b(已知),
例2:如图,已知a//b,那么?2与?4有什么关系呢?为什么?
b
1
2
a
c
4
∴?1=?2(两直线平行,同位角相等).
∵?1+?4=180°(邻补角定义),
∴?2+?4=180°(等量代换).
合作交流
结论:
两条平行线被第三条直线所截,同旁内角互补.
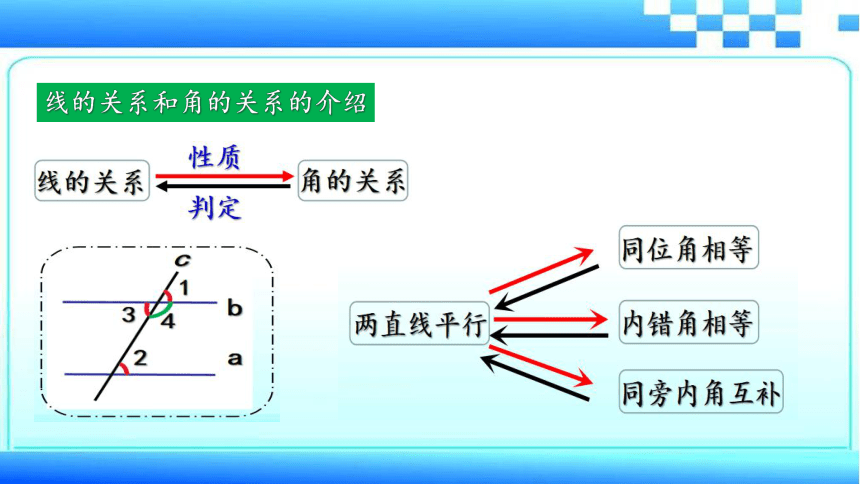
线的关系和角的关系的介绍
1.如图,AD∥BC,∠A=∠C.AB与DC平行吗?为什么?
解:AB∥DC
∵AD∥BC( )
∴∠A=∠ABF( )
∵∠A=∠C( )
∴∠ =∠ ( )
∴ ∥ ( )
反馈练习:
已知
两直线平行,内错角相等
已知
ABF
C
等量代换
AB
DC
同位角相等,两直线平行
2.如图:∠1=∠2,∠3=100°,求∠4.
反馈练习:
解:∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行).
故∠3+∠4=180°
理由是:两直线平行,同旁内角互补.
又∵∠3=100°(已知),∴∠4=80°.
3.已知,如图,a∥b,c∥d,∠1=48°.求∠2、∠3、∠4的度数.
反馈练习:
解:∵c∥d(已知),
∴∠2=∠1=48°(两直线平行,内错角相等).
∵a∥b(已知),∴∠3+∠2=180°,
理由是:两直线平行,同旁内角互补.
故∠3=180°-∠2=132°.
又∵a∥b(已知),∴∠4=∠1=48°
4.如果∠3+∠4=180°,那么∠1与∠2是否相等?为什么?
反馈练习:
解:∵∠3+∠4=180°(已知),
∴a∥b(同旁内角互补,两直线平行).
∵a∥b(已证),∴∠1=∠2,
理由是:两直线平行,同位角相等.
5.如图,如果AB∥CD,∠B=37°,∠D=37°,那么BC与DE平行吗? 为什么?
反馈练习:
解:∵AB∥CD(已知),
∴∠B=∠C=37°,
理由是:两直线平行,内错角相等.
又∵∠D=37°(已知),∴∠C=∠D.
故BC∥DE(内错角相等,两直线平行).
6.如图,已知AB∥CD,∠B=120°,∠D=130°,求∠BED的度数.
反馈练习:
1
2
提示:∠1=180°-∠B=60°,∠2=180°-∠D=50°,∠BED=∠1+∠2.
7.如图在四边形ABCD中,已知AB∥CD,∠B = 60°.
(1)求∠C的度数;
(2)由已知条件能否求得∠A的度数?
解:(1)∵AB∥CD(已知),∴ ∠B+∠C=180°
理由是:两直线平行,同旁内角互补.
又∵∠B=60°(已知),∴∠C=120°(等式的性质).
(2)根据题目的已知条件,无法求出∠A的度数.
反馈练习:
8.小明在纸上画了一个角∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他设计出多少种方法可以测出∠A的度数?
反馈练习:
1
9.如图,OP∥QR∥ST,则下列各式中正确的是( )
A.∠1+∠2+∠3=180°
B.∠1+∠2-∠3=90°
C.∠1-∠2+∠3=90°
D.∠2+∠3-∠1=180°
反馈练习:
D
10.如图,∠1=60?,由点A测点B的方向是( )
A.南偏30? B.北偏西30?
C.南偏东60? D.北偏西60?
反馈练习:
2
C
11.如图,AB∥CD,∠A=60°,∠1=2∠2,求∠2的度数.
反馈练习:
解:∵AB∥CD(已知),
∴∠A+∠ADC=180°,
理由是:两直线平行,同旁内角互补.
即∠A+∠1+∠2=180°.
又∵∠1=2∠2(已知),∴∠A+3∠2=180°.故∠2=40°.
作业:完成课时作业本相应习题.
要求:字迹工整,表述科学.
复习与回顾
(1)∵∠1=∠___,∴a∥b( )
(2)∵∠ =∠2,∴a∥b( )
3
2
同位角相等,两直线平行
内错角相等,两直线平行
根据下图回答下列问题.
(3)∵∠ +∠2= .∴a∥b( )
4
180°
同旁内角互补,两直线平行
1.同位角相等; 2.内错角相等; 3.同旁内角互补
判定条件
如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
思考:
1.在练习本上画两条平行线AB、CD,再画直线EF与直线AB、CD相交.指出图中的同位角、内错角、同旁内角.
数学实验室
2.把图剪成如图所示的四块纸片,分别把图中的每对同位角叠合,你发现了什么?
结论:
图中每对同位角都相等.
由此,我们知道:两条平行直线被第三条直线所截,同位角都相等.
简单说成:两直线平行,同位角相等.
做一做
分别把图中每对内错角叠合,你发现了什么?
把图中的每对同旁内角拼在一起,它们之间有怎样的数量关系?
结论:
图中每对内错角都相等;每对同旁内角都互补.
例1:如图:已知a//b,那么?2与?3相等吗?为什么?
解:∵a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
b
1
2
a
c
3
合作交流
结论:
两条平行线被第三条直线所截,内错角相等.
解:∵a//b(已知),
例2:如图,已知a//b,那么?2与?4有什么关系呢?为什么?
b
1
2
a
c
4
∴?1=?2(两直线平行,同位角相等).
∵?1+?4=180°(邻补角定义),
∴?2+?4=180°(等量代换).
合作交流
结论:
两条平行线被第三条直线所截,同旁内角互补.
线的关系和角的关系的介绍
1.如图,AD∥BC,∠A=∠C.AB与DC平行吗?为什么?
解:AB∥DC
∵AD∥BC( )
∴∠A=∠ABF( )
∵∠A=∠C( )
∴∠ =∠ ( )
∴ ∥ ( )
反馈练习:
已知
两直线平行,内错角相等
已知
ABF
C
等量代换
AB
DC
同位角相等,两直线平行
2.如图:∠1=∠2,∠3=100°,求∠4.
反馈练习:
解:∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行).
故∠3+∠4=180°
理由是:两直线平行,同旁内角互补.
又∵∠3=100°(已知),∴∠4=80°.
3.已知,如图,a∥b,c∥d,∠1=48°.求∠2、∠3、∠4的度数.
反馈练习:
解:∵c∥d(已知),
∴∠2=∠1=48°(两直线平行,内错角相等).
∵a∥b(已知),∴∠3+∠2=180°,
理由是:两直线平行,同旁内角互补.
故∠3=180°-∠2=132°.
又∵a∥b(已知),∴∠4=∠1=48°
4.如果∠3+∠4=180°,那么∠1与∠2是否相等?为什么?
反馈练习:
解:∵∠3+∠4=180°(已知),
∴a∥b(同旁内角互补,两直线平行).
∵a∥b(已证),∴∠1=∠2,
理由是:两直线平行,同位角相等.
5.如图,如果AB∥CD,∠B=37°,∠D=37°,那么BC与DE平行吗? 为什么?
反馈练习:
解:∵AB∥CD(已知),
∴∠B=∠C=37°,
理由是:两直线平行,内错角相等.
又∵∠D=37°(已知),∴∠C=∠D.
故BC∥DE(内错角相等,两直线平行).
6.如图,已知AB∥CD,∠B=120°,∠D=130°,求∠BED的度数.
反馈练习:
1
2
提示:∠1=180°-∠B=60°,∠2=180°-∠D=50°,∠BED=∠1+∠2.
7.如图在四边形ABCD中,已知AB∥CD,∠B = 60°.
(1)求∠C的度数;
(2)由已知条件能否求得∠A的度数?
解:(1)∵AB∥CD(已知),∴ ∠B+∠C=180°
理由是:两直线平行,同旁内角互补.
又∵∠B=60°(已知),∴∠C=120°(等式的性质).
(2)根据题目的已知条件,无法求出∠A的度数.
反馈练习:
8.小明在纸上画了一个角∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他设计出多少种方法可以测出∠A的度数?
反馈练习:
1
9.如图,OP∥QR∥ST,则下列各式中正确的是( )
A.∠1+∠2+∠3=180°
B.∠1+∠2-∠3=90°
C.∠1-∠2+∠3=90°
D.∠2+∠3-∠1=180°
反馈练习:
D
10.如图,∠1=60?,由点A测点B的方向是( )
A.南偏30? B.北偏西30?
C.南偏东60? D.北偏西60?
反馈练习:
2
C
11.如图,AB∥CD,∠A=60°,∠1=2∠2,求∠2的度数.
反馈练习:
解:∵AB∥CD(已知),
∴∠A+∠ADC=180°,
理由是:两直线平行,同旁内角互补.
即∠A+∠1+∠2=180°.
又∵∠1=2∠2(已知),∴∠A+3∠2=180°.故∠2=40°.
作业:完成课时作业本相应习题.
要求:字迹工整,表述科学.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
