苏科版七年级数学下册第12章证明 复习课件(共33张PPT)
文档属性
| 名称 | 苏科版七年级数学下册第12章证明 复习课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 35.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 19:12:59 | ||
图片预览










文档简介
(共33张PPT)
第12章 单元复习
1.对名称或术语的含义进行描述或做出规定,就是给出它们的_____.
知识总结
第12章 单元复习
一、定义与命题
2.判断一件事情的句子叫做___________.
3.在数学中,命题一般由______和______两部分组成.
4.如果条件成立,那么结论成立,这样的命题叫做___________.
5.如果条件成立时,不能保证结论总是正确的,即结论不成立,这样的命题叫做___________.
定义
命题
条件
结论
假命题
真命题
1.根据已知的真命题,确定某个命题真实性的过程叫做___________.
知识总结
二、证明
2.基本事实是其真实性不加以证明的真命题,它是证明其它命题真实性的出发点,经过证明的真命题称为___________.
4.证明的过程通常包含几个推理,每个推理应包括______、_______和__________________.
3.说明一个命题是真命题可以用_________的方法证明,
说明一个命题是假命题可以用_________的方法.
证明
定理
说理
举反例
果
因
由因得果的依据
第12章 单元复习
1.在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做___________.
知识总结
三、互逆命题
3.举出一个符合命题的________,但命题______________的例子来证明命题是假命题,这样的例子称为反例.
2.每个命题都有_________命题.
互逆命题
逆
条件
结论不成立
第12章 单元复习
一、找命题
考点归纳
下列句子中,属于命题的有哪些?
(1)天是蓝的.
(2)延长直线AB.
(3)你吃饭了吗?
(4)今天的天气真好啊!
(5)经过平移,对应线段平行(或在一条直线上)且相等.
(6)如果2,那么.
(1)、 (5) 、(6)
没有判断,不是命题.
疑问句,不是命题.
感叹句,不是命题.
第12章 单元复习
二、假命题与反例
能说明命题“对于任何数a , > a”是假命题的一个反例是( )
A. a= 2
B. a=1
C. a=
D. a=
考点归纳
A
a 或 a
第12章 单元复习
三、命题与逆命题
1.“两负数的商为正数”的条件是_______________________,
结论是_______________________.
2. “等角的补角相等”的逆命题
_________________________________________.
3. 若命题“,不是方程 ax 2y=1的解”为假命题,
则a= _______________________.
考点归纳
两个负数的商
这个商为正数
如果两个角的补角相等,那么这两个角相等
3
第12章 单元复习
三、命题与逆命题
4.下列命题:(1)若,则2 ;
(2)若,则
(3)若,则x=3;
(4)同位角相等
(5)邻补角互补;
(6)无理数是无限小数;
(7)三条边相等的三角形是等边三角形.
其中,原命题与逆命题均为真命题的有_______________________.
考点归纳
(7)
原命题的反例:a=1, b= 2.
逆命题的反例:a= 2.
原命题的反例:x= 3.
原命题和逆命题都是假命题.
逆命题是假命题.
逆命题是假命题.
第12章 单元复习
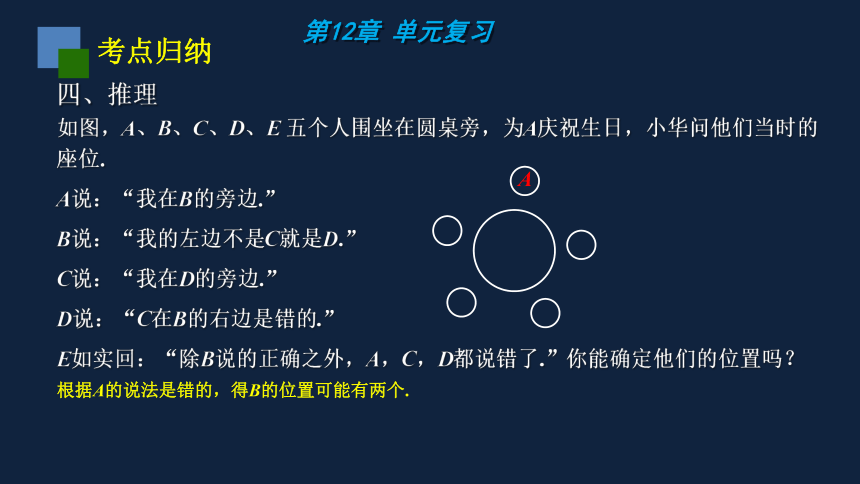
如图,A、B、C、D、E 五个人围坐在圆桌旁,为A庆祝生日,小华问他们当时的座位.
A说:“我在B的旁边.”
B说:“我的左边不是C就是D.”
C说:“我在D的旁边.”
D说:“C在B的右边是错的.”
E如实回:“除B说的正确之外,A,C,D都说错了.”你能确定他们的位置吗?
考点归纳
四、推理
A
根据A的说法是错的,得B的位置可能有两个.
第12章 单元复习
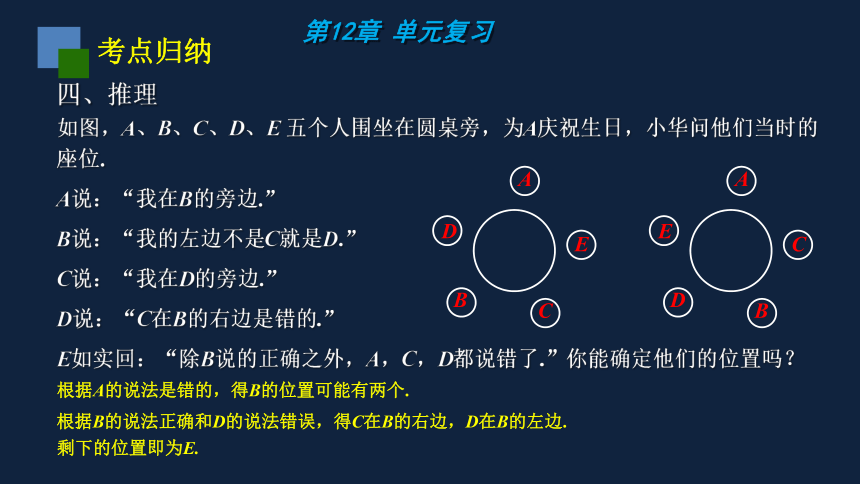
如图,A、B、C、D、E 五个人围坐在圆桌旁,为A庆祝生日,小华问他们当时的座位.
A说:“我在B的旁边.”
B说:“我的左边不是C就是D.”
C说:“我在D的旁边.”
D说:“C在B的右边是错的.”
E如实回:“除B说的正确之外,A,C,D都说错了.”你能确定他们的位置吗?
考点归纳
四、推理
A
E
D
B
C
根据A的说法是错的,得B的位置可能有两个.
A
D
B
C
E
根据B的说法正确和D的说法错误,得C在B的右边,D在B的左边.
剩下的位置即为E.
第12章 单元复习
五、说理证明
例1.如图,已知:AB∥ CD , ∠B=40°, ∠D=40°, 求证: BC∥ DE.
考点归纳
A
B
D
E
C
证明:∵AB∥CD, (已知)
∴ ∠B=∠C,(两直线平行,内错角相等)
∵ ∠B=40°, (已知)
∴ ∠C=40°, (等量代换)
∵ ∠D=40°, (已知)
∴ ∠C=∠ D,(等量代换)
∴ BC∥ DE. (内错角相等,两直线平行)
第12章 单元复习
五、说理证明
练习1:如图,直线AB、CD被直线AE所截,直线AM,EN被MN所截.请你从以下三个条件:①AB∥ CD;②AM ∥ EN; ③∠BAM= ∠CEN中选出两个作为已知条件,另一个作为结论,得出一个正确的命题.
(1)请按照:“∵_______,_______;∴________.”的形式,写出所有正确命题.
(2)在(1)所写的命题中选择一个加以证明,写出推理过程.
考点归纳
A
B
D
E
C
M
N
2
4
1
3
∵①,②
∴③
∵①,③
∴②
∵②,③
∴①
第12章 单元复习
五、说理证明
练习1:如图,直线AB、CD被直线AE所截,直线AM,EN被MN所截.
①AB∥ CD;②AM ∥ EN; ③∠BAM= ∠CEN.
考点归纳
A
B
D
E
C
M
N
2
4
1
3
∵①,②
∴③
证明:∵AB∥CD, (已知)
∴ ∠BAE=∠CEA,(两直线平行,内错角相等)
∵ AM∥EN, (已知)
∴ ∠3=∠4,(两直线平行,内错角相等)
∴ ∠BAE ∠3 =∠CEA ∠4, (等式性质)
即 ∠BAM= ∠CEN
第12章 单元复习
五、说理证明
练习1:如图,直线AB、CD被直线AE所截,直线AM,EN被MN所截.
①AB∥ CD;②AM ∥ EN; ③∠BAM= ∠CEN
考点归纳
A
B
D
E
C
M
N
2
4
1
3
证明:∵AB∥CD, (已知)
∴ ∠BAE=∠CEA,(两直线平行,内错角相等)
∵ ∠BAM= ∠CEN, (已知)
∴∠BAE ∠BAM =∠CEA ∠CEN, (等式性质)
即∠3= ∠4,
∴ AM∥ EN. (内错角相等,两直线平行)
∵①,③
∴②
第12章 单元复习
五、说理证明
练习1:如图,直线AB、CD被直线AE所截,直线AM,EN被MN所截.
①AB∥ CD;②AM ∥ EN; ③∠BAM= ∠CEN
考点归纳
A
B
D
E
C
M
N
2
4
1
3
证明:∵AM∥EN, (已知)
∴ ∠3=∠4,(两直线平行,内错角相等)
∵ ∠BAM= ∠CEN, (已知)
∴∠BAM+∠3 =∠CEN +∠4, (等式性质)
即∠BAE=∠CEA,
∴ AB∥ CD. (内错角相等,两直线平行)
∵②,③
∴①
第12章 单元复习
五、说理证明
练习2:如图,△ABC中,BD是∠ABC的平分线,DE∥ BC交AB于点 E,
∠A=45°, ∠BDC=60°, 求∠AED的度数.
考点归纳
A
B
D
E
C
解:∵ BD是∠ABC的平分线,(已知)
∴ ∠1=∠2,(角平分线的定义)
∵ DE∥BC, (已知)
∴ ∠1=∠3,(两直线平行,内错角相等)
∴ ∠2=∠3,(等量代换)
∴ ∠ AED =∠2 +∠3=2∠2 ,
∵ ∠BDC= ∠2 +∠A, (三角形的外角等于和它不相邻的两个内角的和)
∠A=45°, ∠BDC=60°, (已知)
1
2
3
∴ ∠2=15°,(等式性质)
∴ ∠ AED =2∠2= 30°.
45°
60°
第12章 单元复习
五、说理证明
练习3:如图,BD⊥AC于D,EF ⊥AC于F, ∠AMD = ∠AGF, ∠1 =∠2=35°,
(1)求∠GFC的度数;(2)求证:DM∥ BC.
考点归纳
A
B
F
E
C
G
M
D
H
1
2
3
解:∵ BD⊥AC于D,EF⊥AC于F, (已知)
∴ ∠CDB=∠CFE=90°,(垂直的定义)
∴ DB∥EF, (同位角相等,两直线平行)
∴ ∠1=∠3,(两直线平行,同位角相等)
∵ ∠1=∠2=35°,(已知)
∴ ∠2=∠3=35°, (等量代换)
∴ ∠GFC=∠3+∠CFE=35 +90 =125 ,(等式性质)
GF∥BC, (内错角相等,两直线平行)
∵ ∠AMD =∠AGF, (已知)
∴ MD∥GF, (同位角相等,两直线平行)
∴ DM∥BC. (平行于同一直线的两直线互相平行)
第12章 单元复习
五、说理证明
例2.某机器零件的横截面如图所示,按照要求线段AB和DC的延长线相交成直角才算合格,一工人测得∠A=23°, ∠D=31°, ∠AED=143°,请你帮助他判断该零件是否合格,并说明理由.
考点归纳
A
B
D
E
C
第12章 单元复习
五、说理证明
例2.某机器零件的横截面如图所示,按照要求线段AB和DC的延长线相交成直角才算合格,一工人测得∠A=23°, ∠D=31°, ∠AED=143°,请你帮助他判断该零件是否合格,并说明理由.
考点归纳
A
B
D
E
C
解:
在△AGE中∠AED=∠ A+∠AGE,
在△DHG中∠AGE=∠ H+∠D,
(三角形的外角等于和它不相邻的两个内角的和)
∴∠AED=∠ A+∠H+∠D,
∵ ∠A=23°, ∠D=31°, ∠AED=143 °,
∴ ∠ H = 143 23 31 =89 90 , ∴不合格.
A
D
E
G
H
第12章 单元复习
练习1:如图, ∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F+ ∠G 的度数_____________.
考点归纳
A
D
C
G
B
F
E
五、说理证明
解:连接BF,
2
1
540
则∠A+ ∠G =∠ 1+∠2.
第12章 单元复习
练习2:将△ABC纸片沿着EF折叠,点A的对应点为A’, A’E与BE的夹角为∠1, A’F与CF的夹角为∠2,探索∠A与∠1、 ∠2的数量关系,并说明理由.
考点归纳
A
B
E
F
C
五、说理证明
(2)点A落在四边形EBCF外部的点A’处.
(1)点A落在四边形EBCF内部的点A’处;
1
A
B
E
A’
F
C
2
1
A
B
E
A’
F
C
2
1
A
B
E
A’
F
C
2
第12章 单元复习
考点归纳
1
A
B
E
A’
F
C
2
1
A
B
E
A’
F
C
2
五、说理证明
∠1+∠2 = 2 ∠EAA’+ 2 ∠FAA’
=2(∠EAA’+ ∠FAA’)
=2 ∠EAF,
即∠A=
∠2 ∠1= 2 ∠FAA’ 2 ∠EAA’
=2(∠FAA’ ∠EAA’)
=2∠ EAF ,
即∠A=
∠1 ∠2= 2 ∠EAA’ 2 ∠FAA’
=2(∠EAA’ ∠FAA’)
=2∠ EAF ,
即∠A=
练习2:将△ABC纸片沿着EF折叠,点A的对应点为A’, A’E与BE的夹角为∠1, A’F与CF的夹角为∠2,探索∠A与∠1、 ∠2的数量关系,并说明理由.
(2)点A落在四边形EBCF外部的点A’处.
(1)点A落在四边形EBCF内部的点A’处;
1
A
B
E
A’
F
C
2
第12章 单元复习
四、证明
变式:四边形纸片ABCD中,∠A =160°, ∠B =30°,∠C =60°,
则∠1+∠2+∠3+∠4+ ∠5+∠6+∠7 ∠8=_____________.
考点归纳
A
A’
B
N
B’
D’
H
D
G
Q
C’
C
P
E
M
F
7
8
1
2
3
4
6
5
∵∠8 ∠7=2∠B,
∴ ∠7 ∠8 = 2∠B
∠1+∠2 =2∠A,∠3+∠4 =2∠D,∠5+∠6 =2∠C,
∴ ∠1+∠2+∠3+∠4+ ∠5+∠6+∠7 ∠8
=2( ∠A + ∠D + ∠C ∠B)
=2(360 2 ∠B )
=2(360 2×30)
=600
600
第12章 单元复习
五、说理证明
练习3:如图,(1) 在△ABC纸片中剪去△CED ,得到四边形ABDE,若∠1+∠2=230 ,则剪掉的∠C=______;
考点归纳
C
E
D
A
B
1
2
∠1+∠2 =180 +∠C
50
第12章 单元复习
五、说理证明
练习3:如图,(1) 在△ABC纸片中剪去△CED ,得到四边形ABDE,若∠1+∠2=230 ,则剪掉的∠C=______;
(2)在四边形ABCD中,BP、CP分别平分外角∠CBF、 ∠BCE,设∠A =,
考点归纳
P
D
A
B
C
F
E
H
50
180 +∠H
=90 ∠H
= 90 ( 180 )
=
C
E
D
A
B
1
2
∠1+∠2 =180 +∠C
第12章 单元复习
五、说理证明
练习3:如图,(1) 在△ABC纸片中剪去△CED ,得到四边形ABDE,若∠1+∠2=230 ,则剪掉的∠C=______;
(2)在四边形ABCD中,BP、CP分别平分外角∠BCE、 ∠CBF,设∠A =,
变式1:在四边形ABCD中,BP、CP分别平分内角∠ABC、 ∠DCB,设∠A =,
考点归纳
C
E
D
A
B
1
2
P
D
B
C
P
D
A
B
C
F
E
H
∠1+∠2 =180 +∠C
50
H
180 +∠H
180 +∠H
=90 + ∠H
= 90 + ( 180 )
=
=90 ∠H
= 90 ( 180 )
=
A
第12章 单元复习
五、说理证明
变式2:在四边形ABCD中,BP、CP所在直线分别平分内角∠ABC、 外角∠DCE,设∠A =,
①如图,当180°时,求∠P(用表示);
②当180°时,画出∠P并求∠P(用表示);
③一定存在∠P吗?如果有,直接写出∠P (用表示),如果不一定,指出满足什么条件,并说明理由.
考点归纳
A
B
D
E
C
P
第12章 单元复习
五、说理证明
变式2:在四边形ABCD中,BP、CP所在直线分别平分内角∠ABC、 外角∠DCE,设∠A =,
①如图,当180°时,求∠P(用表示);
考点归纳
A
B
D
E
C
P
H
180 +∠H
= ∠H
= ( 180 )
=
第12章 单元复习
五、说理证明
变式2:在四边形ABCD中,BP、CP所在直线分别平分内角∠ABC、 外角∠DCE,设∠A =,
②当180°时,画出∠P并求∠P(用表示);
考点归纳
第12章 单元复习
五、说理证明
变式2:在四边形ABCD中,BP、CP所在直线分别平分内角∠ABC、 外角∠DCE,设∠A =,
②当180°时,画出∠P并求∠P(用表示);
考点归纳
A
B
D
E
C
P
H
∵360 ()=180 +∠H
= ∠H
=
=
第12章 单元复习
五、说理证明
变式2:在四边形ABCD中,BP、CP所在直线分别平分内角∠ABC、 外角∠DCE,设∠A =,
③一定存在∠P吗?如果有,直接写出∠P (用表示),如果不一定,指出满足什么条件,并说明理由.
考点归纳
A
B
D
E
C
M
N
解:当180°时,AB∥ CD,
∴ ∠ABC= ∠DCE,
∵ BM、CN分别平分内角∠ABC、 外角∠DCE,
∴ ∠MBC= ∠ABC,
∠NCE= ∠DCE,
∴ ∠MBC= ∠NCE,
∴ BM ∥ CN,
∴不存在∠ P.
第12章 单元复习
五、说理证明
变式3:在四边形ABCD和四边形BCM有公共
顶点B、C,且BN平分∠ABC,CM平分∠DCE,
已知∠A +∠M求∠N.
考点归纳
A
B
D
E
C
N
M
H
P
解:∵∠BAD + ∠ADC=180 +∠H,
∠CMN + ∠BNM=180 +∠P ,
= ∠H ,
∴ ∠CMN + ∠BNM 180
= ∠BAD + ∠ADC 180 ) .
∵∠A +∠M ,
∴ ∠N= 85 .
第12章 单元复习
真命题
应用
定理
(推论)
证明
条件
结论
图形:位置、数量
已有知识、经验
已知
辅助线
图形
智慧建构
举反例
命题
假命题
逆命题
互逆
命题
第12章 单元复习
第12章 单元复习
1.对名称或术语的含义进行描述或做出规定,就是给出它们的_____.
知识总结
第12章 单元复习
一、定义与命题
2.判断一件事情的句子叫做___________.
3.在数学中,命题一般由______和______两部分组成.
4.如果条件成立,那么结论成立,这样的命题叫做___________.
5.如果条件成立时,不能保证结论总是正确的,即结论不成立,这样的命题叫做___________.
定义
命题
条件
结论
假命题
真命题
1.根据已知的真命题,确定某个命题真实性的过程叫做___________.
知识总结
二、证明
2.基本事实是其真实性不加以证明的真命题,它是证明其它命题真实性的出发点,经过证明的真命题称为___________.
4.证明的过程通常包含几个推理,每个推理应包括______、_______和__________________.
3.说明一个命题是真命题可以用_________的方法证明,
说明一个命题是假命题可以用_________的方法.
证明
定理
说理
举反例
果
因
由因得果的依据
第12章 单元复习
1.在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做___________.
知识总结
三、互逆命题
3.举出一个符合命题的________,但命题______________的例子来证明命题是假命题,这样的例子称为反例.
2.每个命题都有_________命题.
互逆命题
逆
条件
结论不成立
第12章 单元复习
一、找命题
考点归纳
下列句子中,属于命题的有哪些?
(1)天是蓝的.
(2)延长直线AB.
(3)你吃饭了吗?
(4)今天的天气真好啊!
(5)经过平移,对应线段平行(或在一条直线上)且相等.
(6)如果2,那么.
(1)、 (5) 、(6)
没有判断,不是命题.
疑问句,不是命题.
感叹句,不是命题.
第12章 单元复习
二、假命题与反例
能说明命题“对于任何数a , > a”是假命题的一个反例是( )
A. a= 2
B. a=1
C. a=
D. a=
考点归纳
A
a 或 a
第12章 单元复习
三、命题与逆命题
1.“两负数的商为正数”的条件是_______________________,
结论是_______________________.
2. “等角的补角相等”的逆命题
_________________________________________.
3. 若命题“,不是方程 ax 2y=1的解”为假命题,
则a= _______________________.
考点归纳
两个负数的商
这个商为正数
如果两个角的补角相等,那么这两个角相等
3
第12章 单元复习
三、命题与逆命题
4.下列命题:(1)若,则2 ;
(2)若,则
(3)若,则x=3;
(4)同位角相等
(5)邻补角互补;
(6)无理数是无限小数;
(7)三条边相等的三角形是等边三角形.
其中,原命题与逆命题均为真命题的有_______________________.
考点归纳
(7)
原命题的反例:a=1, b= 2.
逆命题的反例:a= 2.
原命题的反例:x= 3.
原命题和逆命题都是假命题.
逆命题是假命题.
逆命题是假命题.
第12章 单元复习
如图,A、B、C、D、E 五个人围坐在圆桌旁,为A庆祝生日,小华问他们当时的座位.
A说:“我在B的旁边.”
B说:“我的左边不是C就是D.”
C说:“我在D的旁边.”
D说:“C在B的右边是错的.”
E如实回:“除B说的正确之外,A,C,D都说错了.”你能确定他们的位置吗?
考点归纳
四、推理
A
根据A的说法是错的,得B的位置可能有两个.
第12章 单元复习
如图,A、B、C、D、E 五个人围坐在圆桌旁,为A庆祝生日,小华问他们当时的座位.
A说:“我在B的旁边.”
B说:“我的左边不是C就是D.”
C说:“我在D的旁边.”
D说:“C在B的右边是错的.”
E如实回:“除B说的正确之外,A,C,D都说错了.”你能确定他们的位置吗?
考点归纳
四、推理
A
E
D
B
C
根据A的说法是错的,得B的位置可能有两个.
A
D
B
C
E
根据B的说法正确和D的说法错误,得C在B的右边,D在B的左边.
剩下的位置即为E.
第12章 单元复习
五、说理证明
例1.如图,已知:AB∥ CD , ∠B=40°, ∠D=40°, 求证: BC∥ DE.
考点归纳
A
B
D
E
C
证明:∵AB∥CD, (已知)
∴ ∠B=∠C,(两直线平行,内错角相等)
∵ ∠B=40°, (已知)
∴ ∠C=40°, (等量代换)
∵ ∠D=40°, (已知)
∴ ∠C=∠ D,(等量代换)
∴ BC∥ DE. (内错角相等,两直线平行)
第12章 单元复习
五、说理证明
练习1:如图,直线AB、CD被直线AE所截,直线AM,EN被MN所截.请你从以下三个条件:①AB∥ CD;②AM ∥ EN; ③∠BAM= ∠CEN中选出两个作为已知条件,另一个作为结论,得出一个正确的命题.
(1)请按照:“∵_______,_______;∴________.”的形式,写出所有正确命题.
(2)在(1)所写的命题中选择一个加以证明,写出推理过程.
考点归纳
A
B
D
E
C
M
N
2
4
1
3
∵①,②
∴③
∵①,③
∴②
∵②,③
∴①
第12章 单元复习
五、说理证明
练习1:如图,直线AB、CD被直线AE所截,直线AM,EN被MN所截.
①AB∥ CD;②AM ∥ EN; ③∠BAM= ∠CEN.
考点归纳
A
B
D
E
C
M
N
2
4
1
3
∵①,②
∴③
证明:∵AB∥CD, (已知)
∴ ∠BAE=∠CEA,(两直线平行,内错角相等)
∵ AM∥EN, (已知)
∴ ∠3=∠4,(两直线平行,内错角相等)
∴ ∠BAE ∠3 =∠CEA ∠4, (等式性质)
即 ∠BAM= ∠CEN
第12章 单元复习
五、说理证明
练习1:如图,直线AB、CD被直线AE所截,直线AM,EN被MN所截.
①AB∥ CD;②AM ∥ EN; ③∠BAM= ∠CEN
考点归纳
A
B
D
E
C
M
N
2
4
1
3
证明:∵AB∥CD, (已知)
∴ ∠BAE=∠CEA,(两直线平行,内错角相等)
∵ ∠BAM= ∠CEN, (已知)
∴∠BAE ∠BAM =∠CEA ∠CEN, (等式性质)
即∠3= ∠4,
∴ AM∥ EN. (内错角相等,两直线平行)
∵①,③
∴②
第12章 单元复习
五、说理证明
练习1:如图,直线AB、CD被直线AE所截,直线AM,EN被MN所截.
①AB∥ CD;②AM ∥ EN; ③∠BAM= ∠CEN
考点归纳
A
B
D
E
C
M
N
2
4
1
3
证明:∵AM∥EN, (已知)
∴ ∠3=∠4,(两直线平行,内错角相等)
∵ ∠BAM= ∠CEN, (已知)
∴∠BAM+∠3 =∠CEN +∠4, (等式性质)
即∠BAE=∠CEA,
∴ AB∥ CD. (内错角相等,两直线平行)
∵②,③
∴①
第12章 单元复习
五、说理证明
练习2:如图,△ABC中,BD是∠ABC的平分线,DE∥ BC交AB于点 E,
∠A=45°, ∠BDC=60°, 求∠AED的度数.
考点归纳
A
B
D
E
C
解:∵ BD是∠ABC的平分线,(已知)
∴ ∠1=∠2,(角平分线的定义)
∵ DE∥BC, (已知)
∴ ∠1=∠3,(两直线平行,内错角相等)
∴ ∠2=∠3,(等量代换)
∴ ∠ AED =∠2 +∠3=2∠2 ,
∵ ∠BDC= ∠2 +∠A, (三角形的外角等于和它不相邻的两个内角的和)
∠A=45°, ∠BDC=60°, (已知)
1
2
3
∴ ∠2=15°,(等式性质)
∴ ∠ AED =2∠2= 30°.
45°
60°
第12章 单元复习
五、说理证明
练习3:如图,BD⊥AC于D,EF ⊥AC于F, ∠AMD = ∠AGF, ∠1 =∠2=35°,
(1)求∠GFC的度数;(2)求证:DM∥ BC.
考点归纳
A
B
F
E
C
G
M
D
H
1
2
3
解:∵ BD⊥AC于D,EF⊥AC于F, (已知)
∴ ∠CDB=∠CFE=90°,(垂直的定义)
∴ DB∥EF, (同位角相等,两直线平行)
∴ ∠1=∠3,(两直线平行,同位角相等)
∵ ∠1=∠2=35°,(已知)
∴ ∠2=∠3=35°, (等量代换)
∴ ∠GFC=∠3+∠CFE=35 +90 =125 ,(等式性质)
GF∥BC, (内错角相等,两直线平行)
∵ ∠AMD =∠AGF, (已知)
∴ MD∥GF, (同位角相等,两直线平行)
∴ DM∥BC. (平行于同一直线的两直线互相平行)
第12章 单元复习
五、说理证明
例2.某机器零件的横截面如图所示,按照要求线段AB和DC的延长线相交成直角才算合格,一工人测得∠A=23°, ∠D=31°, ∠AED=143°,请你帮助他判断该零件是否合格,并说明理由.
考点归纳
A
B
D
E
C
第12章 单元复习
五、说理证明
例2.某机器零件的横截面如图所示,按照要求线段AB和DC的延长线相交成直角才算合格,一工人测得∠A=23°, ∠D=31°, ∠AED=143°,请你帮助他判断该零件是否合格,并说明理由.
考点归纳
A
B
D
E
C
解:
在△AGE中∠AED=∠ A+∠AGE,
在△DHG中∠AGE=∠ H+∠D,
(三角形的外角等于和它不相邻的两个内角的和)
∴∠AED=∠ A+∠H+∠D,
∵ ∠A=23°, ∠D=31°, ∠AED=143 °,
∴ ∠ H = 143 23 31 =89 90 , ∴不合格.
A
D
E
G
H
第12章 单元复习
练习1:如图, ∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F+ ∠G 的度数_____________.
考点归纳
A
D
C
G
B
F
E
五、说理证明
解:连接BF,
2
1
540
则∠A+ ∠G =∠ 1+∠2.
第12章 单元复习
练习2:将△ABC纸片沿着EF折叠,点A的对应点为A’, A’E与BE的夹角为∠1, A’F与CF的夹角为∠2,探索∠A与∠1、 ∠2的数量关系,并说明理由.
考点归纳
A
B
E
F
C
五、说理证明
(2)点A落在四边形EBCF外部的点A’处.
(1)点A落在四边形EBCF内部的点A’处;
1
A
B
E
A’
F
C
2
1
A
B
E
A’
F
C
2
1
A
B
E
A’
F
C
2
第12章 单元复习
考点归纳
1
A
B
E
A’
F
C
2
1
A
B
E
A’
F
C
2
五、说理证明
∠1+∠2 = 2 ∠EAA’+ 2 ∠FAA’
=2(∠EAA’+ ∠FAA’)
=2 ∠EAF,
即∠A=
∠2 ∠1= 2 ∠FAA’ 2 ∠EAA’
=2(∠FAA’ ∠EAA’)
=2∠ EAF ,
即∠A=
∠1 ∠2= 2 ∠EAA’ 2 ∠FAA’
=2(∠EAA’ ∠FAA’)
=2∠ EAF ,
即∠A=
练习2:将△ABC纸片沿着EF折叠,点A的对应点为A’, A’E与BE的夹角为∠1, A’F与CF的夹角为∠2,探索∠A与∠1、 ∠2的数量关系,并说明理由.
(2)点A落在四边形EBCF外部的点A’处.
(1)点A落在四边形EBCF内部的点A’处;
1
A
B
E
A’
F
C
2
第12章 单元复习
四、证明
变式:四边形纸片ABCD中,∠A =160°, ∠B =30°,∠C =60°,
则∠1+∠2+∠3+∠4+ ∠5+∠6+∠7 ∠8=_____________.
考点归纳
A
A’
B
N
B’
D’
H
D
G
Q
C’
C
P
E
M
F
7
8
1
2
3
4
6
5
∵∠8 ∠7=2∠B,
∴ ∠7 ∠8 = 2∠B
∠1+∠2 =2∠A,∠3+∠4 =2∠D,∠5+∠6 =2∠C,
∴ ∠1+∠2+∠3+∠4+ ∠5+∠6+∠7 ∠8
=2( ∠A + ∠D + ∠C ∠B)
=2(360 2 ∠B )
=2(360 2×30)
=600
600
第12章 单元复习
五、说理证明
练习3:如图,(1) 在△ABC纸片中剪去△CED ,得到四边形ABDE,若∠1+∠2=230 ,则剪掉的∠C=______;
考点归纳
C
E
D
A
B
1
2
∠1+∠2 =180 +∠C
50
第12章 单元复习
五、说理证明
练习3:如图,(1) 在△ABC纸片中剪去△CED ,得到四边形ABDE,若∠1+∠2=230 ,则剪掉的∠C=______;
(2)在四边形ABCD中,BP、CP分别平分外角∠CBF、 ∠BCE,设∠A =,
考点归纳
P
D
A
B
C
F
E
H
50
180 +∠H
=90 ∠H
= 90 ( 180 )
=
C
E
D
A
B
1
2
∠1+∠2 =180 +∠C
第12章 单元复习
五、说理证明
练习3:如图,(1) 在△ABC纸片中剪去△CED ,得到四边形ABDE,若∠1+∠2=230 ,则剪掉的∠C=______;
(2)在四边形ABCD中,BP、CP分别平分外角∠BCE、 ∠CBF,设∠A =,
变式1:在四边形ABCD中,BP、CP分别平分内角∠ABC、 ∠DCB,设∠A =,
考点归纳
C
E
D
A
B
1
2
P
D
B
C
P
D
A
B
C
F
E
H
∠1+∠2 =180 +∠C
50
H
180 +∠H
180 +∠H
=90 + ∠H
= 90 + ( 180 )
=
=90 ∠H
= 90 ( 180 )
=
A
第12章 单元复习
五、说理证明
变式2:在四边形ABCD中,BP、CP所在直线分别平分内角∠ABC、 外角∠DCE,设∠A =,
①如图,当180°时,求∠P(用表示);
②当180°时,画出∠P并求∠P(用表示);
③一定存在∠P吗?如果有,直接写出∠P (用表示),如果不一定,指出满足什么条件,并说明理由.
考点归纳
A
B
D
E
C
P
第12章 单元复习
五、说理证明
变式2:在四边形ABCD中,BP、CP所在直线分别平分内角∠ABC、 外角∠DCE,设∠A =,
①如图,当180°时,求∠P(用表示);
考点归纳
A
B
D
E
C
P
H
180 +∠H
= ∠H
= ( 180 )
=
第12章 单元复习
五、说理证明
变式2:在四边形ABCD中,BP、CP所在直线分别平分内角∠ABC、 外角∠DCE,设∠A =,
②当180°时,画出∠P并求∠P(用表示);
考点归纳
第12章 单元复习
五、说理证明
变式2:在四边形ABCD中,BP、CP所在直线分别平分内角∠ABC、 外角∠DCE,设∠A =,
②当180°时,画出∠P并求∠P(用表示);
考点归纳
A
B
D
E
C
P
H
∵360 ()=180 +∠H
= ∠H
=
=
第12章 单元复习
五、说理证明
变式2:在四边形ABCD中,BP、CP所在直线分别平分内角∠ABC、 外角∠DCE,设∠A =,
③一定存在∠P吗?如果有,直接写出∠P (用表示),如果不一定,指出满足什么条件,并说明理由.
考点归纳
A
B
D
E
C
M
N
解:当180°时,AB∥ CD,
∴ ∠ABC= ∠DCE,
∵ BM、CN分别平分内角∠ABC、 外角∠DCE,
∴ ∠MBC= ∠ABC,
∠NCE= ∠DCE,
∴ ∠MBC= ∠NCE,
∴ BM ∥ CN,
∴不存在∠ P.
第12章 单元复习
五、说理证明
变式3:在四边形ABCD和四边形BCM有公共
顶点B、C,且BN平分∠ABC,CM平分∠DCE,
已知∠A +∠M求∠N.
考点归纳
A
B
D
E
C
N
M
H
P
解:∵∠BAD + ∠ADC=180 +∠H,
∠CMN + ∠BNM=180 +∠P ,
= ∠H ,
∴ ∠CMN + ∠BNM 180
= ∠BAD + ∠ADC 180 ) .
∵∠A +∠M ,
∴ ∠N= 85 .
第12章 单元复习
真命题
应用
定理
(推论)
证明
条件
结论
图形:位置、数量
已有知识、经验
已知
辅助线
图形
智慧建构
举反例
命题
假命题
逆命题
互逆
命题
第12章 单元复习
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
