苏科版数学八年级下册11.1反比例函数课件(共17张PPT)
文档属性
| 名称 | 苏科版数学八年级下册11.1反比例函数课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 21:44:22 | ||
图片预览






文档简介
11.1 反比例函数
1、问题1:现有一张一百元的人民币,如果把它换成50元的人民币,可得几张?换成20元?换成10元?换成5元?换成2元?换成1元?换成0.5元?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}换成的每张面值为x(元)
50
20
10
5
2
1
0.5
x
换成的张数(y)
y
问:1、观察表格可知,当面值由大变小的时候,张数会怎么样变化?
2、你知道在这个过程什么没有变吗?
3、给定变量面值(x),变量张数(y)都有唯一确定的值与它对应吗?
4、张数( y )是面值( x )的函数吗?
因为在这个变化中,两个变量 y 和 x ,给定变量 x的值,变量 y都有唯一确定的值与它对应 ,所以 y 是 x 的函数.
2
5
10
20
50
100
200
2.想一想:用函数关系式表示下列情景中的两个变量之间的关系:
(1)游泳池的容积为5000m3,向池内注水,注满水所需时间t(h)随注水速度v(m3/h)的变化而变化;
(2)用一块体积为300cm3的面团制作拉面,面条的横截面积S(cm2)随面条的长度l (cm)的变化而变化;
(3)某企业为资助贫困学生向教育部门捐赠20万人民币,平均每位贫困学生获赠款额y(万元)随获赠学生的人数x(人)的变化而变化;
(4)实数m与n的积为-78,m随n的变化而变化。
函数关系式
具有什么共同特征?
都是______,等式左边都是单独一个______,等式右边是一个 _____,分子是 _______ ,分母是含有另一个字母变量且次数为_______ 的单项式。
等式
字母变量
分式
常数
1
反比例函数
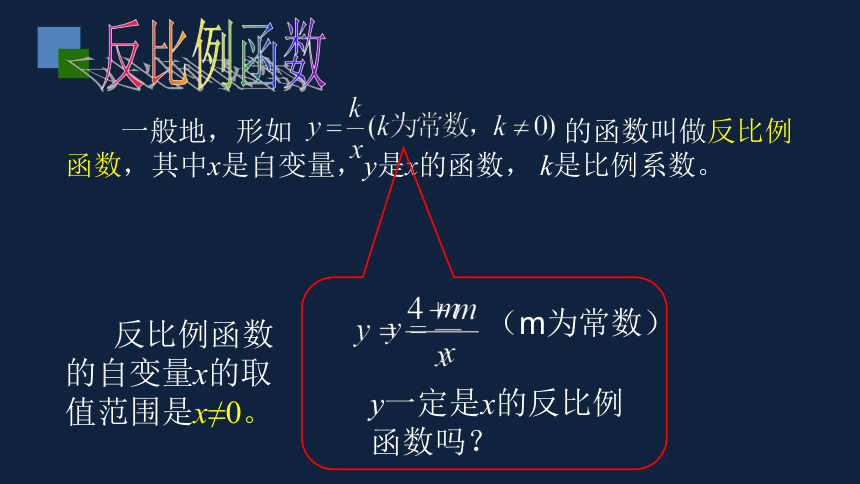
一般地,形如 的函数叫做反比例函数,其中x是自变量,y是x的函数, k是比例系数。
(m为常数)
y一定是x的反比例函数吗?
反比例函数的自变量x的取值范围是x≠0。
例1 下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?
y是x的反比例函数,比例系数k=4。
可以改写成 ,
所以y是x的反比例函数,比例系数k= 。
不具备 的形式,所以y不是x的反比例函数。
不具备 的形式,所以y不是x的反比例函数。
可以改写成 ,
所以y是x的反比例函数,比例系数k=1。
y=kx-1
xy=k
y是x的反比例函数
等价形式:(k≠0)
记住这三种形式
下列函数中,哪些是反比例函数?说出反比例函数的比例系数。
(1)y = -3x; (2)y = 2x+1; (3) ;
(4)y =3x-1;(5) (s是常数,s≠0)
(6) ;(7) ;
概念辨析
1、关系式xy+4=0中y是x的反比例函数吗?
若是,比例系数k等于多少?若不是,请说明理由。
2、在路程s(km) 、速度v(km/h) 、时间t(h)这三个量中,如果 不变,那么 是 的正比例函数;
xy+4=0可以改写成 ,所以y是x的反比例
函数,比例系数k等于-4
如果 不变,那么 是 的反比例函数。
v
或(t)
s
t
或(v)
s
t
v
或(v)
或(t)
例2.当m= 时,关于x的函数y=(m+1)xm2-2是反比例函数?
分析:
{
m2-2=-1
m+1≠0
即
m=±1
m≠-1
{
思考:这个函数能否是关于x的正比例函数?
正比例
变式:函数 ,
当m=_____时, 它是正比例函数,
当m=_____时,它是反比例函数.
正比例函数
反比例函数
例3、已知y与x成反比例,并且当x=3时y=2.
(1)求y与x的函数关系式;
(2)求x=1.5时,y的值;
(3)求y=18时,x的值.
待定系数法
变式:若y与2x-1成反比例,且其图象经过点(1,2),(1)求y与x的函数关系式;
(2)判断点(-2,3)是否在这个函数的图象上?
课堂小结:
一般地,形如 的函数叫做反比例函数,其中x是自变量,y是x的函数, k是比例系数。
待定系数法求函数解析式
y=kx-1
xy=k
一次函数
概念
图象与性质
应用
与一元一次方程、一元一次不等式、二元一次方程组的联系
反比例函数
图象与性质
应用
概念
与分式方程、一次函数的联系
函数
概念
图象与性质
应用
与方程、函数的联系
类比
迁移
知识展望
1、问题1:现有一张一百元的人民币,如果把它换成50元的人民币,可得几张?换成20元?换成10元?换成5元?换成2元?换成1元?换成0.5元?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}换成的每张面值为x(元)
50
20
10
5
2
1
0.5
x
换成的张数(y)
y
问:1、观察表格可知,当面值由大变小的时候,张数会怎么样变化?
2、你知道在这个过程什么没有变吗?
3、给定变量面值(x),变量张数(y)都有唯一确定的值与它对应吗?
4、张数( y )是面值( x )的函数吗?
因为在这个变化中,两个变量 y 和 x ,给定变量 x的值,变量 y都有唯一确定的值与它对应 ,所以 y 是 x 的函数.
2
5
10
20
50
100
200
2.想一想:用函数关系式表示下列情景中的两个变量之间的关系:
(1)游泳池的容积为5000m3,向池内注水,注满水所需时间t(h)随注水速度v(m3/h)的变化而变化;
(2)用一块体积为300cm3的面团制作拉面,面条的横截面积S(cm2)随面条的长度l (cm)的变化而变化;
(3)某企业为资助贫困学生向教育部门捐赠20万人民币,平均每位贫困学生获赠款额y(万元)随获赠学生的人数x(人)的变化而变化;
(4)实数m与n的积为-78,m随n的变化而变化。
函数关系式
具有什么共同特征?
都是______,等式左边都是单独一个______,等式右边是一个 _____,分子是 _______ ,分母是含有另一个字母变量且次数为_______ 的单项式。
等式
字母变量
分式
常数
1
反比例函数
一般地,形如 的函数叫做反比例函数,其中x是自变量,y是x的函数, k是比例系数。
(m为常数)
y一定是x的反比例函数吗?
反比例函数的自变量x的取值范围是x≠0。
例1 下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?
y是x的反比例函数,比例系数k=4。
可以改写成 ,
所以y是x的反比例函数,比例系数k= 。
不具备 的形式,所以y不是x的反比例函数。
不具备 的形式,所以y不是x的反比例函数。
可以改写成 ,
所以y是x的反比例函数,比例系数k=1。
y=kx-1
xy=k
y是x的反比例函数
等价形式:(k≠0)
记住这三种形式
下列函数中,哪些是反比例函数?说出反比例函数的比例系数。
(1)y = -3x; (2)y = 2x+1; (3) ;
(4)y =3x-1;(5) (s是常数,s≠0)
(6) ;(7) ;
概念辨析
1、关系式xy+4=0中y是x的反比例函数吗?
若是,比例系数k等于多少?若不是,请说明理由。
2、在路程s(km) 、速度v(km/h) 、时间t(h)这三个量中,如果 不变,那么 是 的正比例函数;
xy+4=0可以改写成 ,所以y是x的反比例
函数,比例系数k等于-4
如果 不变,那么 是 的反比例函数。
v
或(t)
s
t
或(v)
s
t
v
或(v)
或(t)
例2.当m= 时,关于x的函数y=(m+1)xm2-2是反比例函数?
分析:
{
m2-2=-1
m+1≠0
即
m=±1
m≠-1
{
思考:这个函数能否是关于x的正比例函数?
正比例
变式:函数 ,
当m=_____时, 它是正比例函数,
当m=_____时,它是反比例函数.
正比例函数
反比例函数
例3、已知y与x成反比例,并且当x=3时y=2.
(1)求y与x的函数关系式;
(2)求x=1.5时,y的值;
(3)求y=18时,x的值.
待定系数法
变式:若y与2x-1成反比例,且其图象经过点(1,2),(1)求y与x的函数关系式;
(2)判断点(-2,3)是否在这个函数的图象上?
课堂小结:
一般地,形如 的函数叫做反比例函数,其中x是自变量,y是x的函数, k是比例系数。
待定系数法求函数解析式
y=kx-1
xy=k
一次函数
概念
图象与性质
应用
与一元一次方程、一元一次不等式、二元一次方程组的联系
反比例函数
图象与性质
应用
概念
与分式方程、一次函数的联系
函数
概念
图象与性质
应用
与方程、函数的联系
类比
迁移
知识展望
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
