苏科版数学八年级下册专题复习 9.3 平行四边形的判定与性质 课件(共25张PPT)
文档属性
| 名称 | 苏科版数学八年级下册专题复习 9.3 平行四边形的判定与性质 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 21:45:56 | ||
图片预览





文档简介
专题复行四边形的判定与性质
苏科版八年级下册
数学
1.
熟练掌握平行四边形的性质、判定;
学习目标
2.会利用平行四边形的性质、判定解决有关的计算、
证明问题;
3.在解决问题的过程中,提高分析问题、解决问题
的能力.
热身训练
A
D
B
C
1
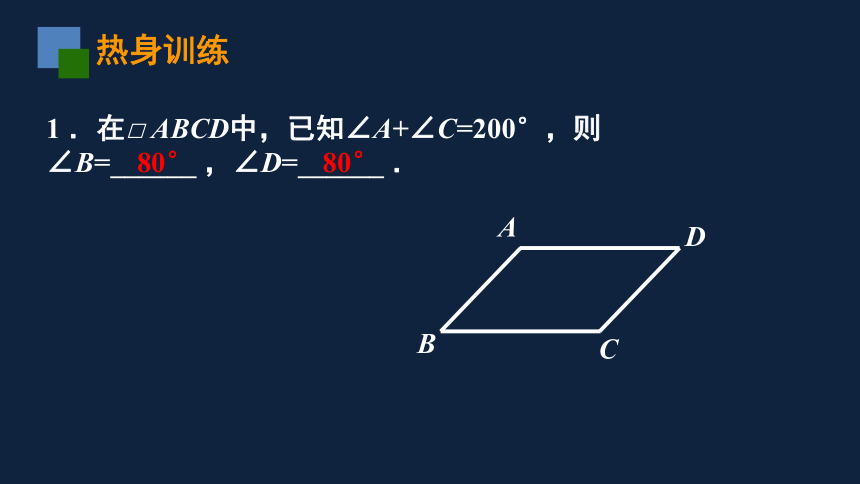
.在□
ABCD中,已知∠A+∠C=200°,则∠B=______
,∠D=______
.
80°
80°
热身训练
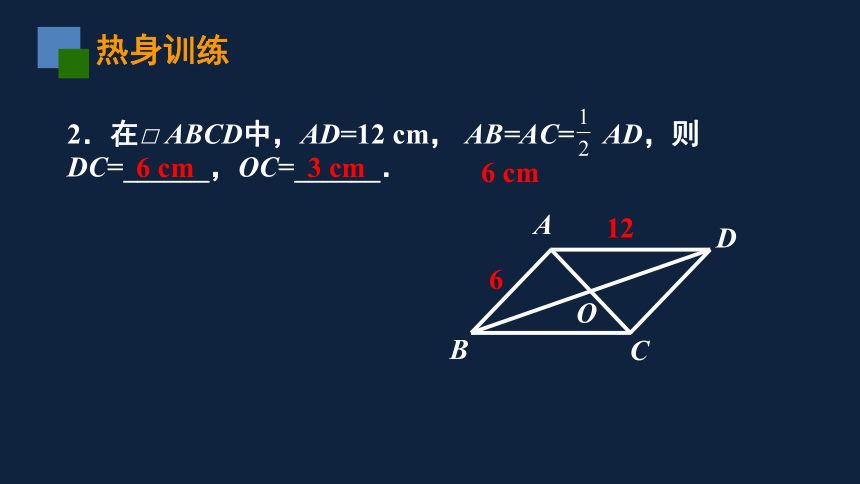
2.在□
ABCD中,AD=12
cm,
AB=AC=
AD,则DC=______,OC=______.
A
D
B
C
O
6
cm
3
cm
12
6
6
cm
A
D
B
C
O
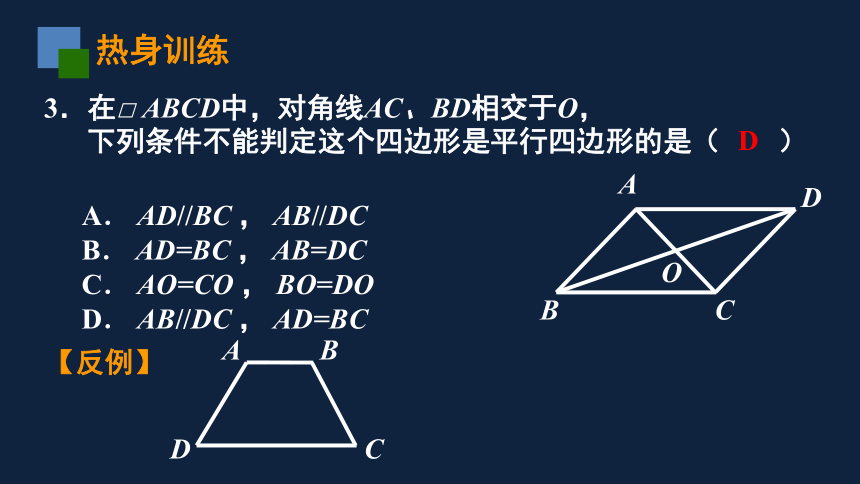
3.在□
ABCD中,对角线AC、BD相交于O,
下列条件不能判定这个四边形是平行四边形的是(
)
A.
AD//BC
,
AB//DC
B.
AD=BC
,
AB=DC
C.
AO=CO
,
BO=DO
D.
AB//DC
,
AD=BC
D
【反例】
A
D
B
C
热身训练
平行四边形的概念:
两组对边分别平行的四边形是平行四边形
知识梳理
平行四边形的性质
两组对边分别平行
从边看
对称性:平行四边形是中心对称图形
平行四边形
两组对边分别相等
从角看
两组对角相等
邻角互补
从对角线看:对角线互相平分
知识梳理
典例分析
例1
如图,平行四边形ABCD中,对角线AC,BD相交于O,
AC=8,BD=10,则边AB的取值范围是(
)
A
D
B
C
O
在△ABO中,
BO
?AO<AB<BO+AO
∴1<AB<9
B
A.8<AB<10
B.1<AB<9
C.4<AB<5
D.2<AB<18
平行四边形对角线互相平分
OA=
AC=4,OB=
BD=5
小提示:看到条件中出现平行四边形,要学会自然联想到平行四边形的一些性质
【简析】
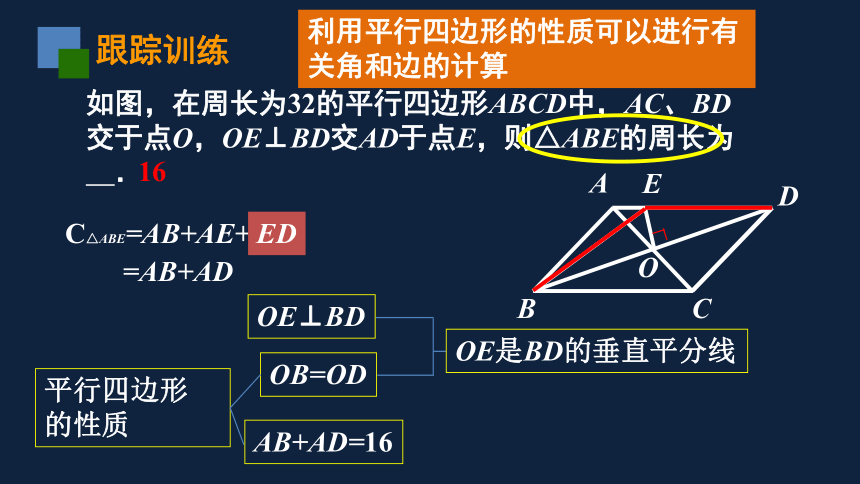
如图,在周长为32的平行四边形ABCD中,AC、BD交于点O,OE⊥BD交AD于点E,则△ABE的周长为
.
A
D
B
C
O
E
跟踪训练
C△ABE=AB+AE+BE
平行四边形
的性质
OE⊥BD
OE是BD的垂直平分线
OB=OD
AB+AD=16
16
ED
=AB+AD
利用平行四边形的性质可以进行有关角和边的计算
平行四边形的判定
两组对边分别平行的四边形是平行四边形
边
两组对边分别相等的四边形是平行四边形
对角线:对角线互相平分的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
知识梳理
判定
例2
在四边形ABCD中,AB∥CD,请你添加一
个条件,使得四边形ABCD成为平行四边
形,你添加的条件是____________
.
A
D
B
C
典例分析
开放型题
AB
//
CD
AD
//
BC
□ABCD
AB
=
CD
一组对边平行且相等的四边形是平行四边形
两组对边分别平行的四边形是平行四边形
∠A+∠B=180°
∠A
=∠C
……
【简析】
例3
已知:如图,在□
ABCD中,BE平分∠ABC,
DF平分∠ADC.
求证:BE=DF.
典例分析
A
D
B
C
E
F
方法一
△ABE
≌△
CDF
AB
=
CD
∠A=∠C
□ABCD
∠1
=
∠2
∠ABC=∠ADC
∠1=
∠ABC
∠2=
∠ADC
【简析】
1
2
例3
已知:如图,在□
ABCD中,BE平分∠ABC,
DF平分∠ADC.
求证:BE=DF.
典例分析
A
D
B
C
E
F
方法二:
□
ABCD
AD
//
BC
AE=CF
BE
=
DF
□
BFDE
ED
=
BF
AE=AB
CD=CF
【简析】
1
2
3
例3
已知:如图,在□
ABCD中,BE平分∠ABC,
DF平分∠ADC.
求证:BE=DF.
典例分析
A
D
B
C
E
F
方法三:
□
ABCD
AD
//
BC
∠3=∠5
BE
=
DF
□
BFDE
EB
//
DF
【简析】
1
2
3
4
5
例3
已知:如图,在□
ABCD中,BE平分∠ABC,
DF平分∠ADC.
求证:BE=DF.
典例分析
A
D
B
C
E
F
证明:∵四边形ABCD是平行四边形
∴
∠ABC=∠ADC,AD
//
BC
∴
∠4=∠5
∵
BE平分∠ABC,
DF平分∠ADC
∴
∠3=
∠4
∴
EB
//
DF
又∵
ED//
BF
∴四边形EBFD是平行四边形
∴BE
=
DF
∴
∠3=
∠ABC,∠4=
∠ADC
解题方法不唯一,多种角度看问题
1
2
3
4
5
∴
∠3=
∠5
回顾反思
证明线段相等的方法可以有:
①证明三角形全等
②利用平行四边形的性质
例4
如图,在□
ABCD中,点E是边AD的中点,
BE的延长线与CD的延长线相交于点F,连接BD、AF
.
(1)求证:四边形ABDF是平行四边形;
(2)求证:CF=2AB;
(3)试探究:当BC、CD满足怎样
的数量关系时,CE⊥BF.
A
D
B
C
E
F
典例分析
例4
如图,在□
ABCD中,点E是边AD的中点,
BE的延长线与CD的延长线相交于点F,连接BD、AF
.
(1)求证:四边形ABDF是平行四边形;
A
D
B
C
E
F
典例分析
□ABCD
【简析】
AB
//
DC
2
1
△ABE≌△DFE
BE
=
EF
典例分析
证明:∵四边形ABCD是平行四边形
∴
AB
//
CD
∴
∠1=∠2
∵
点E是AD的中点
∴
AE=DE
在△ABE和△DFE中
∴
△ABE≌△DFE(ASA)
∴四边形ABDF是平行四边形
∴BE
=
EF
∠BEA=∠FED
∠1=∠2
AE=DE
又∵AE=DE
还可以用其他方法判定
平行四边形吗?
A
D
B
C
E
F
2
1
例4
如图,在□
ABCD中,点E是边AD的中点,
BE的延长线与CD的延长线相交于点F,连接BD、AF
.
(1)求证:四边形ABDF是平行四边形;
(2)求证:CF=2AB;
A
D
B
C
E
F
典例分析
□ABDF
【简析】
AB
=
DF
□ABCD
AB
=
DC
CF
=
DC+DF
=AB+AB
=2AB
例4
如图,在□
ABCD中,点E是边AD的中点,
BE的延长线与CD的延长线相交于点F,连接BD、AF
.
(3)试探究:当BC、CD满足怎样
的数量关系时,CE⊥BF.
典例分析
B
A
D
C
E
F
□ABDF
【简析】
BE
=
EF
CF=BC
CF=2AB
BC=2AB=2CD
证明:∵四边形ABDF是平行四边形
典例分析
当BC=2CD时,
CE⊥BF
∴BE
=
EF
由(2)得,CF=2AB
又∵BC=2CD
即BC=2AB
∴CF=BC
在等腰三角形BCF中,BE
=
EF
CE⊥BF
B
A
C
E
F
变式
在□
ABCD中,BC=2AB,E
是AD的中点,
求证:CE⊥BE
典例分析
A
D
B
C
E
【简析】
□ABCD,BC=2AB
AB=AE
∠1=∠2
1
2
AD
//
BC
3
4
∠1=∠3
∴∠3+∠4=
×180°=90°
小提示:平行线+等腰三角形→角平分线
∠3=
∠ABC
同理∠4=
∠BCD
课堂小结
1.综合运用平行四边形的性质和判定解决计算一些
角度、长度,证明线段相等、线段的数量关系、位置
关系等问题时,基础是对相关知识要熟悉,它们之间
有一定的联系;
2.在解题方法较多的情况下,要考虑择优、择简!
苏科版八年级下册
数学
1.
熟练掌握平行四边形的性质、判定;
学习目标
2.会利用平行四边形的性质、判定解决有关的计算、
证明问题;
3.在解决问题的过程中,提高分析问题、解决问题
的能力.
热身训练
A
D
B
C
1
.在□
ABCD中,已知∠A+∠C=200°,则∠B=______
,∠D=______
.
80°
80°
热身训练
2.在□
ABCD中,AD=12
cm,
AB=AC=
AD,则DC=______,OC=______.
A
D
B
C
O
6
cm
3
cm
12
6
6
cm
A
D
B
C
O
3.在□
ABCD中,对角线AC、BD相交于O,
下列条件不能判定这个四边形是平行四边形的是(
)
A.
AD//BC
,
AB//DC
B.
AD=BC
,
AB=DC
C.
AO=CO
,
BO=DO
D.
AB//DC
,
AD=BC
D
【反例】
A
D
B
C
热身训练
平行四边形的概念:
两组对边分别平行的四边形是平行四边形
知识梳理
平行四边形的性质
两组对边分别平行
从边看
对称性:平行四边形是中心对称图形
平行四边形
两组对边分别相等
从角看
两组对角相等
邻角互补
从对角线看:对角线互相平分
知识梳理
典例分析
例1
如图,平行四边形ABCD中,对角线AC,BD相交于O,
AC=8,BD=10,则边AB的取值范围是(
)
A
D
B
C
O
在△ABO中,
BO
?AO<AB<BO+AO
∴1<AB<9
B
A.8<AB<10
B.1<AB<9
C.4<AB<5
D.2<AB<18
平行四边形对角线互相平分
OA=
AC=4,OB=
BD=5
小提示:看到条件中出现平行四边形,要学会自然联想到平行四边形的一些性质
【简析】
如图,在周长为32的平行四边形ABCD中,AC、BD交于点O,OE⊥BD交AD于点E,则△ABE的周长为
.
A
D
B
C
O
E
跟踪训练
C△ABE=AB+AE+BE
平行四边形
的性质
OE⊥BD
OE是BD的垂直平分线
OB=OD
AB+AD=16
16
ED
=AB+AD
利用平行四边形的性质可以进行有关角和边的计算
平行四边形的判定
两组对边分别平行的四边形是平行四边形
边
两组对边分别相等的四边形是平行四边形
对角线:对角线互相平分的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
知识梳理
判定
例2
在四边形ABCD中,AB∥CD,请你添加一
个条件,使得四边形ABCD成为平行四边
形,你添加的条件是____________
.
A
D
B
C
典例分析
开放型题
AB
//
CD
AD
//
BC
□ABCD
AB
=
CD
一组对边平行且相等的四边形是平行四边形
两组对边分别平行的四边形是平行四边形
∠A+∠B=180°
∠A
=∠C
……
【简析】
例3
已知:如图,在□
ABCD中,BE平分∠ABC,
DF平分∠ADC.
求证:BE=DF.
典例分析
A
D
B
C
E
F
方法一
△ABE
≌△
CDF
AB
=
CD
∠A=∠C
□ABCD
∠1
=
∠2
∠ABC=∠ADC
∠1=
∠ABC
∠2=
∠ADC
【简析】
1
2
例3
已知:如图,在□
ABCD中,BE平分∠ABC,
DF平分∠ADC.
求证:BE=DF.
典例分析
A
D
B
C
E
F
方法二:
□
ABCD
AD
//
BC
AE=CF
BE
=
DF
□
BFDE
ED
=
BF
AE=AB
CD=CF
【简析】
1
2
3
例3
已知:如图,在□
ABCD中,BE平分∠ABC,
DF平分∠ADC.
求证:BE=DF.
典例分析
A
D
B
C
E
F
方法三:
□
ABCD
AD
//
BC
∠3=∠5
BE
=
DF
□
BFDE
EB
//
DF
【简析】
1
2
3
4
5
例3
已知:如图,在□
ABCD中,BE平分∠ABC,
DF平分∠ADC.
求证:BE=DF.
典例分析
A
D
B
C
E
F
证明:∵四边形ABCD是平行四边形
∴
∠ABC=∠ADC,AD
//
BC
∴
∠4=∠5
∵
BE平分∠ABC,
DF平分∠ADC
∴
∠3=
∠4
∴
EB
//
DF
又∵
ED//
BF
∴四边形EBFD是平行四边形
∴BE
=
DF
∴
∠3=
∠ABC,∠4=
∠ADC
解题方法不唯一,多种角度看问题
1
2
3
4
5
∴
∠3=
∠5
回顾反思
证明线段相等的方法可以有:
①证明三角形全等
②利用平行四边形的性质
例4
如图,在□
ABCD中,点E是边AD的中点,
BE的延长线与CD的延长线相交于点F,连接BD、AF
.
(1)求证:四边形ABDF是平行四边形;
(2)求证:CF=2AB;
(3)试探究:当BC、CD满足怎样
的数量关系时,CE⊥BF.
A
D
B
C
E
F
典例分析
例4
如图,在□
ABCD中,点E是边AD的中点,
BE的延长线与CD的延长线相交于点F,连接BD、AF
.
(1)求证:四边形ABDF是平行四边形;
A
D
B
C
E
F
典例分析
□ABCD
【简析】
AB
//
DC
2
1
△ABE≌△DFE
BE
=
EF
典例分析
证明:∵四边形ABCD是平行四边形
∴
AB
//
CD
∴
∠1=∠2
∵
点E是AD的中点
∴
AE=DE
在△ABE和△DFE中
∴
△ABE≌△DFE(ASA)
∴四边形ABDF是平行四边形
∴BE
=
EF
∠BEA=∠FED
∠1=∠2
AE=DE
又∵AE=DE
还可以用其他方法判定
平行四边形吗?
A
D
B
C
E
F
2
1
例4
如图,在□
ABCD中,点E是边AD的中点,
BE的延长线与CD的延长线相交于点F,连接BD、AF
.
(1)求证:四边形ABDF是平行四边形;
(2)求证:CF=2AB;
A
D
B
C
E
F
典例分析
□ABDF
【简析】
AB
=
DF
□ABCD
AB
=
DC
CF
=
DC+DF
=AB+AB
=2AB
例4
如图,在□
ABCD中,点E是边AD的中点,
BE的延长线与CD的延长线相交于点F,连接BD、AF
.
(3)试探究:当BC、CD满足怎样
的数量关系时,CE⊥BF.
典例分析
B
A
D
C
E
F
□ABDF
【简析】
BE
=
EF
CF=BC
CF=2AB
BC=2AB=2CD
证明:∵四边形ABDF是平行四边形
典例分析
当BC=2CD时,
CE⊥BF
∴BE
=
EF
由(2)得,CF=2AB
又∵BC=2CD
即BC=2AB
∴CF=BC
在等腰三角形BCF中,BE
=
EF
CE⊥BF
B
A
C
E
F
变式
在□
ABCD中,BC=2AB,E
是AD的中点,
求证:CE⊥BE
典例分析
A
D
B
C
E
【简析】
□ABCD,BC=2AB
AB=AE
∠1=∠2
1
2
AD
//
BC
3
4
∠1=∠3
∴∠3+∠4=
×180°=90°
小提示:平行线+等腰三角形→角平分线
∠3=
∠ABC
同理∠4=
∠BCD
课堂小结
1.综合运用平行四边形的性质和判定解决计算一些
角度、长度,证明线段相等、线段的数量关系、位置
关系等问题时,基础是对相关知识要熟悉,它们之间
有一定的联系;
2.在解题方法较多的情况下,要考虑择优、择简!
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
