苏科版数学八年级下册专题课件:9.4正方形及特殊平行四边形综合(共18张PPT)
文档属性
| 名称 | 苏科版数学八年级下册专题课件:9.4正方形及特殊平行四边形综合(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 22:10:58 | ||
图片预览

文档简介
[专题复习]
正方形及特殊平行四边形综合
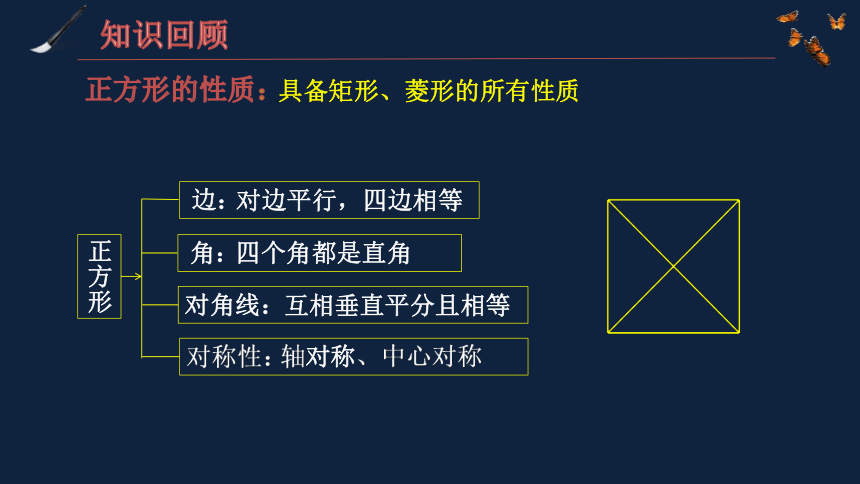
知识回顾
正方形的性质:
具备矩形、菱形的所有性质
边:
角:
对称性:
正方形
对角线:
对边平行,四边相等
四个角都是直角
互相垂直平分且相等
轴对称、中心对称
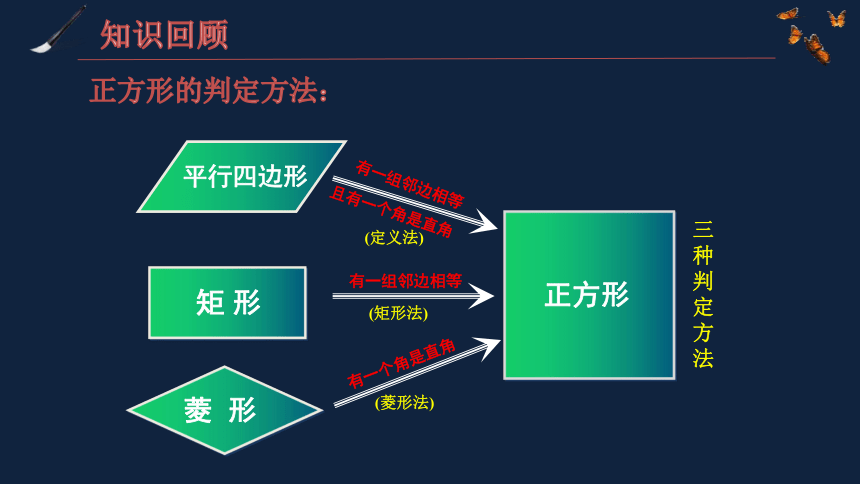
矩 形
菱 形
正方形
平行四边形
且有一个角是直角
有一组邻边相等
(定义法)
有一组邻边相等
(矩形法)
有一个角是直角
(菱形法)
知识回顾
正方形的判定方法:
三种判定方法
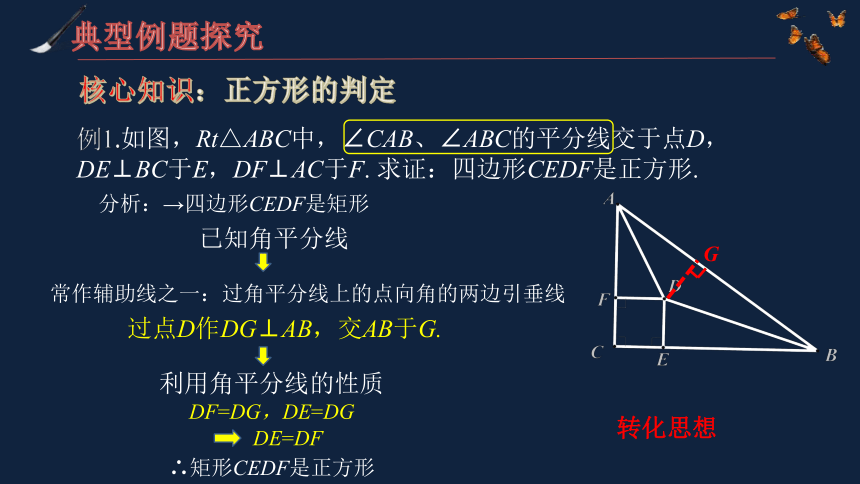
例1.如图,Rt△ABC中,∠CAB、∠ABC的平分线交于点D,DE⊥BC于E,DF⊥AC于F. 求证:四边形CEDF是正方形.
G
过点D作DG⊥AB,交AB于G.
利用角平分线的性质
DF=DG,DE=DG
转化思想
核心知识:正方形的判定
典型例题探究
已知角平分线
分析:→四边形CEDF是矩形
DE=DF
∴矩形CEDF是正方形
常作辅助线之一:过角平分线上的点向角的两边引垂线
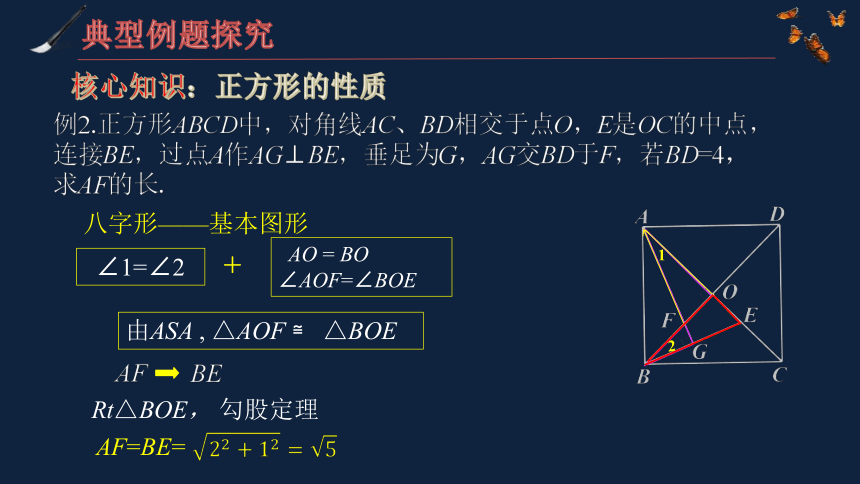
核心知识:正方形的性质
典型例题探究
例2.正方形ABCD中,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AG⊥BE,垂足为G,AG交BD于F,若BD=4,
求AF的长.
AF
BE
八字形——基本图形
∠1=∠2
1
2
Rt△BOE, 勾股定理
由ASA , △AOF ≌ △BOE
AF=BE=
+
AO = BO
∠AOF=∠BOE
知识考点:正方形的性质
典型例题探究
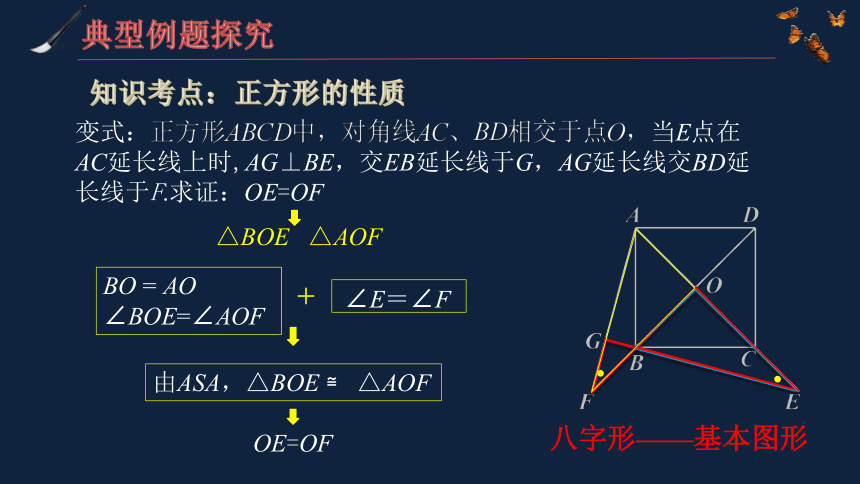
变式:正方形ABCD中,对角线AC、BD相交于点O,当E点在AC延长线上时,AG⊥BE,交EB延长线于G,AG延长线交BD延长线于F.求证:OE=OF
八字形——基本图形
△BOE △AOF
BO = AO
∠BOE=∠AOF
+
由ASA,△BOE ≌ △AOF
∠E=∠F
OE=OF
核心知识:正方形的性质
典型例题探究
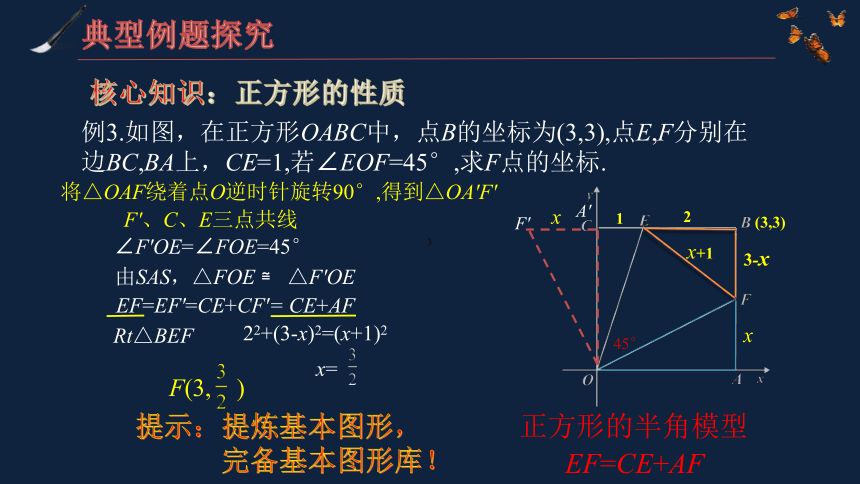
例3.如图,在正方形OABC中,点B的坐标为(3,3),点E,F分别在边BC,BA上,CE=1,若∠EOF=45°,求F点的坐标.
由SAS,△FOE ≌ △F'OE
2
3-x
x
x
x+1
Rt△BEF
22+(3-x)2=(x+1)2
正方形的半角模型
1
(3,3)
45°
x=
F(3, )
EF=CE+AF
F'
A'
提示:提炼基本图形,
完备基本图形库!
∠F'OE=∠FOE=45°
将△OAF绕着点O逆时针旋转90°,得到△OA'F'
F'、C、E三点共线
EF=EF'=CE+CF'= CE+AF
知识再建构
四边形
边
平行四边形
矩形
边角
正方形
菱形
定义
性质
判定
应用
特殊平行四边形综合
典型例题探究
例4.如图,在△ABC中,AD是边BC上的中线,过点A作AE//BC,过点D作DE//AB,DE与AC、AE分别交于点O、点E,连接EC.
(1)证明AD=EC.
四边形ABDE为平行四边形
AD=EC
BD=CD
AE=CD
四边形ADCE为平行四边形
AE=BD
特殊平行四边形综合
典型例题探究
(2)当∠BAC=90°时,判断四边形ADCE的形状;
(3)当△ABC满足什么条件时,四边形ADCE是矩形;
(4)当△ABC满足什么条件时,四边形ADCE是正方形.
(2) 直角三角形斜边上的中线等于斜边的一半
AD=DC
菱形
(3)等腰三角形三线合一
AB=AC
(4)∠BAC=90°且AB=AC
由(1),四边形ADCE为平行四边形
特殊平行四边形综合
发展思维——运动问题
例4.在矩形ABCD 中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,当其中一个动点到达后就停止运动.
(1)若G,H分别是AB,DC中点,求证:四边形EGFH始终是平行四边形.
t
t
∴四边形EGFH为平行四边形.
4
3
分析:
由SAS,得△AEG ≌ △CFH
AE=CF=t
EG=FH
由SAS,得△GFA ≌ △HEC
GF=HE
∠EAG=∠FCH
特殊平行四边形综合
在矩形ABCD 中,AB=3,BC=4,E,F是对角线 AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,当其中一个动点到达后就停止运动.
(2)在(1)条件下,当 t为何值时,四边形 EGFH为矩形.
t
t
3
4
连接GH, GH= EF
①如图1,E、F相遇前
EF=AC-AE-CF
EF=5-t-t
4=5-t-t
t=0.5s
运动问题,注意相对位置的改变
②如图2,E、F相遇后
AE=CF=t
EF=AE-AF=t-(5-t)
4=t-(5-t)
t=4.5s
图1
4
3
图2
∴t=0.5s或4.5s时,四边形EGFH为矩形.
分类讨论
发展思维——运动问题
四边形GBCH为平行四边形
GH=BC=4
4
AC=5
特殊平行四边形综合
在矩形ABCD 中,AB=3,BC=4,E,F是对角线 AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,当其中一个动点到达后就停止运动.
(3)若 G,H分别从A、C出发在折线 A-B-C,C-D-A上运动,与 E,F 以相同的速度同时出发。当t为何值时,四边形 EGFH为菱形.
G
H
发展思维——运动问题
作EF的中垂线
即为AC的中垂线
特殊平行四边形综合
在矩形ABCD 中,AB=3,BC=4,E,F是对角线 AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,当其中一个动点到达后就停止运动.
(3)若 G,H分别从A、C出发在折线 A-B-C,C-D-A上运动,若 G,H与 E,F 以相同的速度同时出发,当t为何值时,四边形 EGFH为菱形.
BG=DH= t-3
AH=GC=7-t
∵GH为AC的中垂线,
∴AG=GC=AH=HC=7-t
4
3
∴32+(t-3)2=(7-t)2
3
在Rt△ABG中,
AB2+BG2=AG2
发展思维——运动问题
7-t
t-3
7-t
t-3
∴t=
7-t
分析:
∴ 当 t= 时,四边形 EGFH为菱形.
梳理总结
一、知识:
掌握平行四边形、矩形、菱形、正方形的性质和判定
二、方法:
1.提炼基本图形
2.研究动点问题策略:
抓住动点运动的临界点,利用特殊平行四边形的性质,将动态问题先分割成几个静态问题;寻找等量关系,将几何问题转化成代数——方程问题。
注意相对位置的变化,要分类讨论.
三、思想:转化思想、分类讨论思想、方程思想
八字形、正方形的半角模型......
再遇特殊平行四边形。。。
课后作业
课后作业
祝同学们学习进步!
正方形及特殊平行四边形综合
知识回顾
正方形的性质:
具备矩形、菱形的所有性质
边:
角:
对称性:
正方形
对角线:
对边平行,四边相等
四个角都是直角
互相垂直平分且相等
轴对称、中心对称
矩 形
菱 形
正方形
平行四边形
且有一个角是直角
有一组邻边相等
(定义法)
有一组邻边相等
(矩形法)
有一个角是直角
(菱形法)
知识回顾
正方形的判定方法:
三种判定方法
例1.如图,Rt△ABC中,∠CAB、∠ABC的平分线交于点D,DE⊥BC于E,DF⊥AC于F. 求证:四边形CEDF是正方形.
G
过点D作DG⊥AB,交AB于G.
利用角平分线的性质
DF=DG,DE=DG
转化思想
核心知识:正方形的判定
典型例题探究
已知角平分线
分析:→四边形CEDF是矩形
DE=DF
∴矩形CEDF是正方形
常作辅助线之一:过角平分线上的点向角的两边引垂线
核心知识:正方形的性质
典型例题探究
例2.正方形ABCD中,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AG⊥BE,垂足为G,AG交BD于F,若BD=4,
求AF的长.
AF
BE
八字形——基本图形
∠1=∠2
1
2
Rt△BOE, 勾股定理
由ASA , △AOF ≌ △BOE
AF=BE=
+
AO = BO
∠AOF=∠BOE
知识考点:正方形的性质
典型例题探究
变式:正方形ABCD中,对角线AC、BD相交于点O,当E点在AC延长线上时,AG⊥BE,交EB延长线于G,AG延长线交BD延长线于F.求证:OE=OF
八字形——基本图形
△BOE △AOF
BO = AO
∠BOE=∠AOF
+
由ASA,△BOE ≌ △AOF
∠E=∠F
OE=OF
核心知识:正方形的性质
典型例题探究
例3.如图,在正方形OABC中,点B的坐标为(3,3),点E,F分别在边BC,BA上,CE=1,若∠EOF=45°,求F点的坐标.
由SAS,△FOE ≌ △F'OE
2
3-x
x
x
x+1
Rt△BEF
22+(3-x)2=(x+1)2
正方形的半角模型
1
(3,3)
45°
x=
F(3, )
EF=CE+AF
F'
A'
提示:提炼基本图形,
完备基本图形库!
∠F'OE=∠FOE=45°
将△OAF绕着点O逆时针旋转90°,得到△OA'F'
F'、C、E三点共线
EF=EF'=CE+CF'= CE+AF
知识再建构
四边形
边
平行四边形
矩形
边角
正方形
菱形
定义
性质
判定
应用
特殊平行四边形综合
典型例题探究
例4.如图,在△ABC中,AD是边BC上的中线,过点A作AE//BC,过点D作DE//AB,DE与AC、AE分别交于点O、点E,连接EC.
(1)证明AD=EC.
四边形ABDE为平行四边形
AD=EC
BD=CD
AE=CD
四边形ADCE为平行四边形
AE=BD
特殊平行四边形综合
典型例题探究
(2)当∠BAC=90°时,判断四边形ADCE的形状;
(3)当△ABC满足什么条件时,四边形ADCE是矩形;
(4)当△ABC满足什么条件时,四边形ADCE是正方形.
(2) 直角三角形斜边上的中线等于斜边的一半
AD=DC
菱形
(3)等腰三角形三线合一
AB=AC
(4)∠BAC=90°且AB=AC
由(1),四边形ADCE为平行四边形
特殊平行四边形综合
发展思维——运动问题
例4.在矩形ABCD 中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,当其中一个动点到达后就停止运动.
(1)若G,H分别是AB,DC中点,求证:四边形EGFH始终是平行四边形.
t
t
∴四边形EGFH为平行四边形.
4
3
分析:
由SAS,得△AEG ≌ △CFH
AE=CF=t
EG=FH
由SAS,得△GFA ≌ △HEC
GF=HE
∠EAG=∠FCH
特殊平行四边形综合
在矩形ABCD 中,AB=3,BC=4,E,F是对角线 AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,当其中一个动点到达后就停止运动.
(2)在(1)条件下,当 t为何值时,四边形 EGFH为矩形.
t
t
3
4
连接GH, GH= EF
①如图1,E、F相遇前
EF=AC-AE-CF
EF=5-t-t
4=5-t-t
t=0.5s
运动问题,注意相对位置的改变
②如图2,E、F相遇后
AE=CF=t
EF=AE-AF=t-(5-t)
4=t-(5-t)
t=4.5s
图1
4
3
图2
∴t=0.5s或4.5s时,四边形EGFH为矩形.
分类讨论
发展思维——运动问题
四边形GBCH为平行四边形
GH=BC=4
4
AC=5
特殊平行四边形综合
在矩形ABCD 中,AB=3,BC=4,E,F是对角线 AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,当其中一个动点到达后就停止运动.
(3)若 G,H分别从A、C出发在折线 A-B-C,C-D-A上运动,与 E,F 以相同的速度同时出发。当t为何值时,四边形 EGFH为菱形.
G
H
发展思维——运动问题
作EF的中垂线
即为AC的中垂线
特殊平行四边形综合
在矩形ABCD 中,AB=3,BC=4,E,F是对角线 AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,当其中一个动点到达后就停止运动.
(3)若 G,H分别从A、C出发在折线 A-B-C,C-D-A上运动,若 G,H与 E,F 以相同的速度同时出发,当t为何值时,四边形 EGFH为菱形.
BG=DH= t-3
AH=GC=7-t
∵GH为AC的中垂线,
∴AG=GC=AH=HC=7-t
4
3
∴32+(t-3)2=(7-t)2
3
在Rt△ABG中,
AB2+BG2=AG2
发展思维——运动问题
7-t
t-3
7-t
t-3
∴t=
7-t
分析:
∴ 当 t= 时,四边形 EGFH为菱形.
梳理总结
一、知识:
掌握平行四边形、矩形、菱形、正方形的性质和判定
二、方法:
1.提炼基本图形
2.研究动点问题策略:
抓住动点运动的临界点,利用特殊平行四边形的性质,将动态问题先分割成几个静态问题;寻找等量关系,将几何问题转化成代数——方程问题。
注意相对位置的变化,要分类讨论.
三、思想:转化思想、分类讨论思想、方程思想
八字形、正方形的半角模型......
再遇特殊平行四边形。。。
课后作业
课后作业
祝同学们学习进步!
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
