苏科版数学七年级下9.5.1 因式分解 课件 (27张PPT)
文档属性
| 名称 | 苏科版数学七年级下9.5.1 因式分解 课件 (27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 175.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 21:46:49 | ||
图片预览








文档简介
9.5 多项式的因式分解(1)
教学情境
(1)计算:375×2.8+375×4.9+375×2.3
解:原式=375×(2.8+4.9+2.3)
=375×10
=3750
(2)由上面的计算,类似的,ab+ac+ad又能写成什么形式呢?
概念1 公因式:
我们把多项式ab+ac+ad中各项都含有的因式___,
叫做这个多项式的公因式。
练一练.
下列多项式的各项是否公因式?如果有,请找出公因式。
(1)a2b+ab2;
(2) 3x2 ? 6x3
(3) 9abc?6a2b2+12abc2.
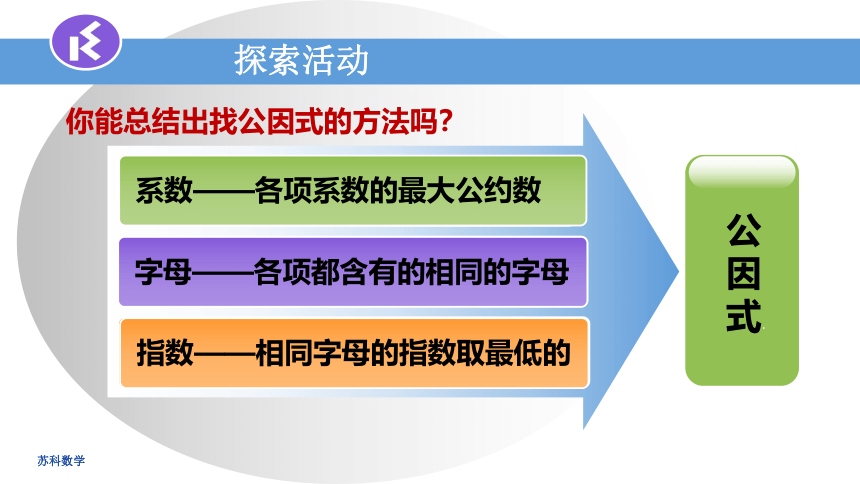
探索活动
系数——
字母——
指数——
公因式.
系数——各项系数的最大公约数
字母——各项都含有的相同的字母
指数——相同字母的指数取最低的
你能总结出找公因式的方法吗?
概念2 因式分解:
m(a+b+c)=ma+mb+mc,这种运算属于______,
而 ma+mb+mc=m(a+b+c),
像这样,把一个多项式写成几个整式的积的形式,叫做多项式的因式分解.
注意点:
(1)和差形式转化为乘积形式.
(2)必须是整式的积
(3)因式分解与整式乘法是一个互逆的变形过程。
(1)(a +1)(a?1) = a2?1;
(2)a2?1 = (a +1)(a?1) ;
(3)8a2b3c = 2a2·2b3·2c ;
(4) x2+2x+6=x(x+2)+6;
(5)
下列各式由左边到右边的变形,哪些是因式分解,哪些不是?
辨析:
不是
是
不是
不是
不是
教学情境
下列各式由左边到右边的变形,哪些是因式分解,哪些不是?为什么?
(1)ab+ac+d=a(b+c)+d ;
(2)a2?1=(a +1)(a?1) ;
(3)(a +1)(a?1) = a2?1;
(4)3x2?2x?1=(3x+1)(x?1) .
不是
是
不是
是
在下列等式中,从左到右的变形是因式分解的有( )
①
②
③
④
⑤
⑥2
③
⑥
概念3 提公因式法.
如果多项式的各项含有公因式,那么就可以把这个公因式提到括号外,把多项式写成公因式与另一个多项式的积的形式,这种分解因式的方法叫做提公因式法.
ma+mb+mc
ma+mb+mc
公因式
把多项式写成公因式与另一个多项式的积的形式,这种分解因式的方法叫做 提公因式法 。
m
=
(a+b+c)
例: 找 3 x 2 – 6 xy 的公因式。
系数:最大
公约数。
3
字母:相同的字母
x
所以,公因式是3x。
指数:相同字母的最低次幂
1
找出下列多项式各项的公因式.
(1)a2b+ab2
(2)3x2 ? 6x3;
(3) 9abc?6a2b2+12abc2 ;
ab
3ab
3x2
尝试解决
例1 把5x3?10x2分解因式.
尝试解决
例2.把?15x3y?10x2y2+5x2y分解因式.
?当多项式的第一项的系数是“?”时,通常把“?”作为公因式的负号写在括号外,使括号内第一项的系数化为“+ ”.
?提公因式法因式分解的关键就是找公因式.
(1) 6m2n-9mn2+15mn ;
(2) 3x3-6x2y+3x ;
(3) ? x2y+4xy ? 5y .
把下列各式分解因式:
巩固练习1:
系数——各项系数的最大公约数
字母——各项都含有的相同的字母
指数——相同字母的指数取最低的
各项系数都是整数
找公因式
尝试解决
例3 把3a(x+y)?2b(x+y) 分解因式.
公因式不仅是单项式,还可以是多项式.
尝试解决
变式:把3a(x?y)?2b(y?x) 分解因式.
底数互为相反数,在化为同底过程中要注意指数的奇偶性与幂的符号的关系.
这里 (x ? y)2=(y ? x)2 , ( x ? y)3=?(y ? x)3.
练习:
将下列各式因式分解
(1)3m(x-y)-mn(x-y)
(2)(2a +b)(3a-3b)-(3a-b)(2a+b)
(3) 5(x-y) 3 +10y(y-x)2
1.已知a+b=-4,ab=2,求a2b+ab2的值.
2.试说明 82018 - 82017 一定能被7整除.
四、拓展提升
小结思考
1.什么叫公因式?如何找公因式?
2.什么叫因式分解?因式分解与整式乘法有什么区别和联系?
教学情境
几个整式的积
一个多项式
因式分解
整式乘法
整式乘法与因式分解是互逆变形.
整式乘法与因式分解的区别与联系:
小结思考
1.什么叫公因式?如何找公因式?
2.什么叫因式分解?因式分解与整式乘法有什么
区别和联系?
3.如何用提公因式法进行因式分解?
4.分解因式要进行到每个因式都不能再分解为止.
把下列各式分解因式
(1) (x ? y)3x+(y ? x)3y ;
(2) (a ? b)2 (2a+b) + (b ? a)2 (a+2b) .
思考:
课后作业
4.思考:
(1)20042+2004能被2005整除吗?
(2)如果n是自然数,那么n2+n是奇数还是偶数?
1.完成因式分解一,不能打印的同学请认真抄题目.小组长在今天下午五点前交给我,小组四号在今天晚上九点前交给我,其余同学交到小组群里,订正情况小组长跟进一下.
3.周四下午评讲乘法公式和因式分解相关题目,自己可以汇总需要讲的题目,下午统计.
教学情境
(1)计算:375×2.8+375×4.9+375×2.3
解:原式=375×(2.8+4.9+2.3)
=375×10
=3750
(2)由上面的计算,类似的,ab+ac+ad又能写成什么形式呢?
概念1 公因式:
我们把多项式ab+ac+ad中各项都含有的因式___,
叫做这个多项式的公因式。
练一练.
下列多项式的各项是否公因式?如果有,请找出公因式。
(1)a2b+ab2;
(2) 3x2 ? 6x3
(3) 9abc?6a2b2+12abc2.
探索活动
系数——
字母——
指数——
公因式.
系数——各项系数的最大公约数
字母——各项都含有的相同的字母
指数——相同字母的指数取最低的
你能总结出找公因式的方法吗?
概念2 因式分解:
m(a+b+c)=ma+mb+mc,这种运算属于______,
而 ma+mb+mc=m(a+b+c),
像这样,把一个多项式写成几个整式的积的形式,叫做多项式的因式分解.
注意点:
(1)和差形式转化为乘积形式.
(2)必须是整式的积
(3)因式分解与整式乘法是一个互逆的变形过程。
(1)(a +1)(a?1) = a2?1;
(2)a2?1 = (a +1)(a?1) ;
(3)8a2b3c = 2a2·2b3·2c ;
(4) x2+2x+6=x(x+2)+6;
(5)
下列各式由左边到右边的变形,哪些是因式分解,哪些不是?
辨析:
不是
是
不是
不是
不是
教学情境
下列各式由左边到右边的变形,哪些是因式分解,哪些不是?为什么?
(1)ab+ac+d=a(b+c)+d ;
(2)a2?1=(a +1)(a?1) ;
(3)(a +1)(a?1) = a2?1;
(4)3x2?2x?1=(3x+1)(x?1) .
不是
是
不是
是
在下列等式中,从左到右的变形是因式分解的有( )
①
②
③
④
⑤
⑥2
③
⑥
概念3 提公因式法.
如果多项式的各项含有公因式,那么就可以把这个公因式提到括号外,把多项式写成公因式与另一个多项式的积的形式,这种分解因式的方法叫做提公因式法.
ma+mb+mc
ma+mb+mc
公因式
把多项式写成公因式与另一个多项式的积的形式,这种分解因式的方法叫做 提公因式法 。
m
=
(a+b+c)
例: 找 3 x 2 – 6 xy 的公因式。
系数:最大
公约数。
3
字母:相同的字母
x
所以,公因式是3x。
指数:相同字母的最低次幂
1
找出下列多项式各项的公因式.
(1)a2b+ab2
(2)3x2 ? 6x3;
(3) 9abc?6a2b2+12abc2 ;
ab
3ab
3x2
尝试解决
例1 把5x3?10x2分解因式.
尝试解决
例2.把?15x3y?10x2y2+5x2y分解因式.
?当多项式的第一项的系数是“?”时,通常把“?”作为公因式的负号写在括号外,使括号内第一项的系数化为“+ ”.
?提公因式法因式分解的关键就是找公因式.
(1) 6m2n-9mn2+15mn ;
(2) 3x3-6x2y+3x ;
(3) ? x2y+4xy ? 5y .
把下列各式分解因式:
巩固练习1:
系数——各项系数的最大公约数
字母——各项都含有的相同的字母
指数——相同字母的指数取最低的
各项系数都是整数
找公因式
尝试解决
例3 把3a(x+y)?2b(x+y) 分解因式.
公因式不仅是单项式,还可以是多项式.
尝试解决
变式:把3a(x?y)?2b(y?x) 分解因式.
底数互为相反数,在化为同底过程中要注意指数的奇偶性与幂的符号的关系.
这里 (x ? y)2=(y ? x)2 , ( x ? y)3=?(y ? x)3.
练习:
将下列各式因式分解
(1)3m(x-y)-mn(x-y)
(2)(2a +b)(3a-3b)-(3a-b)(2a+b)
(3) 5(x-y) 3 +10y(y-x)2
1.已知a+b=-4,ab=2,求a2b+ab2的值.
2.试说明 82018 - 82017 一定能被7整除.
四、拓展提升
小结思考
1.什么叫公因式?如何找公因式?
2.什么叫因式分解?因式分解与整式乘法有什么区别和联系?
教学情境
几个整式的积
一个多项式
因式分解
整式乘法
整式乘法与因式分解是互逆变形.
整式乘法与因式分解的区别与联系:
小结思考
1.什么叫公因式?如何找公因式?
2.什么叫因式分解?因式分解与整式乘法有什么
区别和联系?
3.如何用提公因式法进行因式分解?
4.分解因式要进行到每个因式都不能再分解为止.
把下列各式分解因式
(1) (x ? y)3x+(y ? x)3y ;
(2) (a ? b)2 (2a+b) + (b ? a)2 (a+2b) .
思考:
课后作业
4.思考:
(1)20042+2004能被2005整除吗?
(2)如果n是自然数,那么n2+n是奇数还是偶数?
1.完成因式分解一,不能打印的同学请认真抄题目.小组长在今天下午五点前交给我,小组四号在今天晚上九点前交给我,其余同学交到小组群里,订正情况小组长跟进一下.
3.周四下午评讲乘法公式和因式分解相关题目,自己可以汇总需要讲的题目,下午统计.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
