苏科版数学七年级下册 第七章 平面图形的认识(二)第三节 7.3图形的平移课件 20张ppt
文档属性
| 名称 | 苏科版数学七年级下册 第七章 平面图形的认识(二)第三节 7.3图形的平移课件 20张ppt |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 21:53:25 | ||
图片预览






文档简介
7.3 图形的平移
感受生活中的平移
你还能举出生活中类似的例子吗?
想一想
根据这些现象,你能说说什么样的图形运动称为平移?
在平面内,将一个图形沿着某个方向移动一定的距离,叫做图形的平移.
定义:
图形在平移过程中,对于运动主体(图形)哪些因素发生了变化?
哪些保持不变?
改变的是位置;不变的是形状和大小.
平移两要素:方向和距离.
1.在以下现象中,其中是平移的是( )
①水管里水的流动;
②滑雪运动员在平坦的雪地上滑行;
③射出的子弹;
④火车在笔直的铁轨上行驶.
A.①② B.①③ C.②③ D.②④
D
反馈练习:
反馈练习:
2.下列所示的图案分别是奔驰、奥迪、大众、三菱汽车的车标,其中,可以看作由“基本图案经”过平移得到的是( )
A
B
C
D
B
例1.在所示的方格纸上,将线段AB向左平移4格,得到线段A'B'.再将线段A'B'向上平移3格,得到线段A″B″.连接对应点的线段AA'与BB',A'A″与B'B″,AA″与BB″.
在连接对应点的线段的过程中,你有什么发现?
探索发现
对应点连线平行且相等.
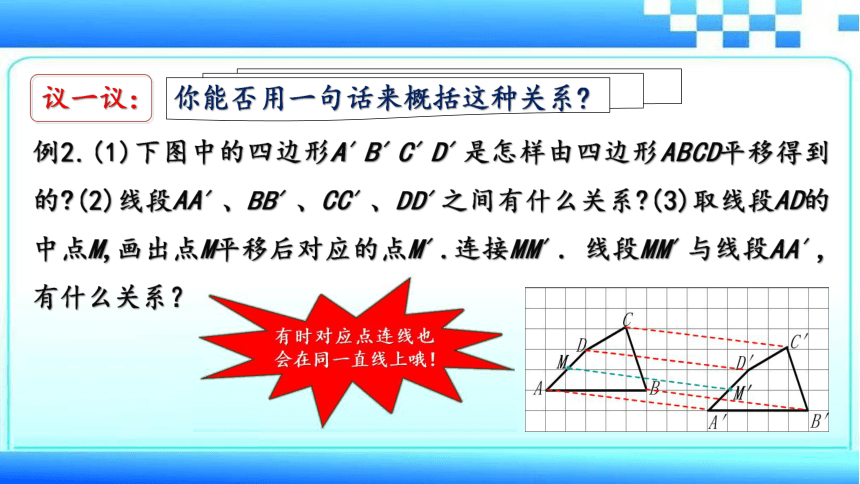
例2.(1)下图中的四边形A′B′C′D′是怎样由四边形ABCD平移得到的?(2)线段AA′、BB′、CC′、DD′之间有什么关系?(3)取线段AD的中点M,画出点M平移后对应的点M′.连接MM′.线段MM′与线段AA′,有什么关系?
你能否用一句话来概括这种关系?
议一议:
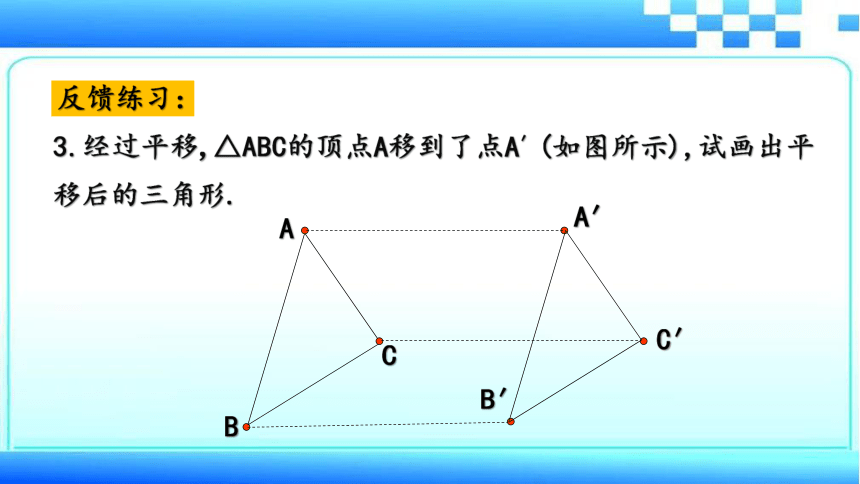
3.经过平移,△ABC的顶点A移到了点A′(如图所示),试画出平移后的三角形.
A
B
C
A′
反馈练习:
C′
B′
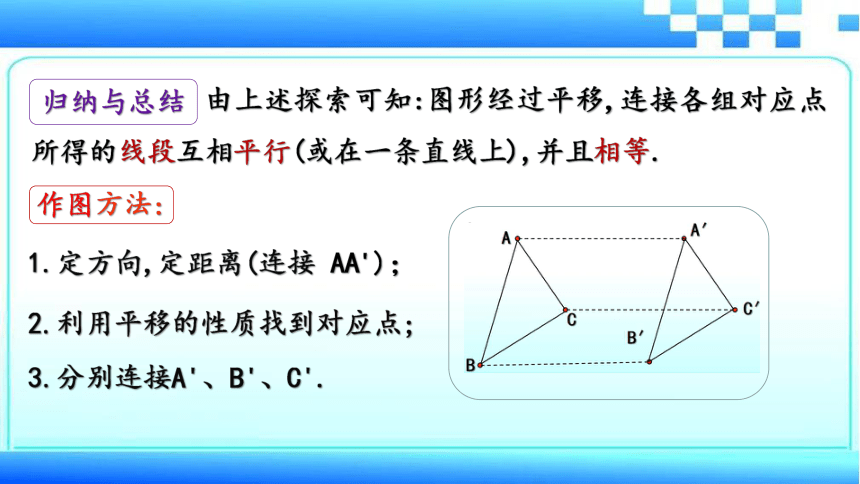
由上述探索可知:图形经过平移,连接各组对应点所得的线段互相平行(或在一条直线上),并且相等.
归纳与总结
作图方法:
1.定方向,定距离(连接 AA');
2.利用平移的性质找到对应点;
3.分别连接A'、B'、C'.
反馈练习:
4.平移方格纸中的图形,使点A平移到点A'处,画出平移后的图形.
提示:A点可按先向右边平移4个格,再向上平移1格,得到A'点,(图形上的其它点也可按相同的方式得到).
5.平移必须具备的两个要素是:①平移的______;②平移的______.
平移只改变图形的 ,不改变图形的形状、大小.
平移前后对应的线段_____且_____,对应角大小_______.
反馈练习:
方向
距离
位置
平行
相等
不变
反馈练习:
6.如图所示,平移△ABC可得到△DEF,如果∠A=50°,∠C=60°,那么∠E= ,∠EDF= ,∠F= ,∠DOB= .
70°
50°
60°
60°
反馈练习:
7.如图,△A'B'C'是由△ABC沿射线AC方向平移2cm得到,若AC=3cm则A'C= .
(提示:A'C=AC-AA')
1cm
8.看图思考以下问题:
(2)电梯里的小明上升了5米,电梯里的其他人做了怎样的运动?
注意:“图形移动”意味着“图形上的每个点都沿同一个方向移动相同的距离”.
反馈练习:
(1)电梯在上升过程中做了什么运动?
9.图中的4个小三角形都是等边三角形,边长为2cm,你能通过平移三角形ABC得到其他三角形吗?若能,请画出平移的方向,并说出平移的距离.
反馈练习:
△ABC沿着BA的方向平移2cm即可得到△FAE;
△ABC沿着BC的方向平移2cm即可得到△ECD.
10.如图所示,下列四组图形中,有一组中的两个经过平移其中一个能得到另一个,这组图形是( ).
反馈练习:
A
A
B
C
D
11.某公园计划在一块长方形草坪上修两条人行横道,修建方案如图所示,求剩余草坪的面积.
反馈练习:
(7–2)×(4–1)=15m2
12.如下图中,有一块长为32m,宽24m的长方形的草坪,其中有两条宽2m的直道把草坪分为四块,则草坪的面积是多少?
反馈练习:
(32-2)×(24-2)=660m2
13.如图,在一块长为20m,宽为8m的长方形的草地上,有一条弯曲的小路(小路任何地方的水平宽度都是0.5m).请你猜想草地的面积是多少?
反馈练习:
(20–0.5)×8=156 m2
作业:完成课时作业本相应习题.
要求:字迹工整,表述科学.
感受生活中的平移
你还能举出生活中类似的例子吗?
想一想
根据这些现象,你能说说什么样的图形运动称为平移?
在平面内,将一个图形沿着某个方向移动一定的距离,叫做图形的平移.
定义:
图形在平移过程中,对于运动主体(图形)哪些因素发生了变化?
哪些保持不变?
改变的是位置;不变的是形状和大小.
平移两要素:方向和距离.
1.在以下现象中,其中是平移的是( )
①水管里水的流动;
②滑雪运动员在平坦的雪地上滑行;
③射出的子弹;
④火车在笔直的铁轨上行驶.
A.①② B.①③ C.②③ D.②④
D
反馈练习:
反馈练习:
2.下列所示的图案分别是奔驰、奥迪、大众、三菱汽车的车标,其中,可以看作由“基本图案经”过平移得到的是( )
A
B
C
D
B
例1.在所示的方格纸上,将线段AB向左平移4格,得到线段A'B'.再将线段A'B'向上平移3格,得到线段A″B″.连接对应点的线段AA'与BB',A'A″与B'B″,AA″与BB″.
在连接对应点的线段的过程中,你有什么发现?
探索发现
对应点连线平行且相等.
例2.(1)下图中的四边形A′B′C′D′是怎样由四边形ABCD平移得到的?(2)线段AA′、BB′、CC′、DD′之间有什么关系?(3)取线段AD的中点M,画出点M平移后对应的点M′.连接MM′.线段MM′与线段AA′,有什么关系?
你能否用一句话来概括这种关系?
议一议:
3.经过平移,△ABC的顶点A移到了点A′(如图所示),试画出平移后的三角形.
A
B
C
A′
反馈练习:
C′
B′
由上述探索可知:图形经过平移,连接各组对应点所得的线段互相平行(或在一条直线上),并且相等.
归纳与总结
作图方法:
1.定方向,定距离(连接 AA');
2.利用平移的性质找到对应点;
3.分别连接A'、B'、C'.
反馈练习:
4.平移方格纸中的图形,使点A平移到点A'处,画出平移后的图形.
提示:A点可按先向右边平移4个格,再向上平移1格,得到A'点,(图形上的其它点也可按相同的方式得到).
5.平移必须具备的两个要素是:①平移的______;②平移的______.
平移只改变图形的 ,不改变图形的形状、大小.
平移前后对应的线段_____且_____,对应角大小_______.
反馈练习:
方向
距离
位置
平行
相等
不变
反馈练习:
6.如图所示,平移△ABC可得到△DEF,如果∠A=50°,∠C=60°,那么∠E= ,∠EDF= ,∠F= ,∠DOB= .
70°
50°
60°
60°
反馈练习:
7.如图,△A'B'C'是由△ABC沿射线AC方向平移2cm得到,若AC=3cm则A'C= .
(提示:A'C=AC-AA')
1cm
8.看图思考以下问题:
(2)电梯里的小明上升了5米,电梯里的其他人做了怎样的运动?
注意:“图形移动”意味着“图形上的每个点都沿同一个方向移动相同的距离”.
反馈练习:
(1)电梯在上升过程中做了什么运动?
9.图中的4个小三角形都是等边三角形,边长为2cm,你能通过平移三角形ABC得到其他三角形吗?若能,请画出平移的方向,并说出平移的距离.
反馈练习:
△ABC沿着BA的方向平移2cm即可得到△FAE;
△ABC沿着BC的方向平移2cm即可得到△ECD.
10.如图所示,下列四组图形中,有一组中的两个经过平移其中一个能得到另一个,这组图形是( ).
反馈练习:
A
A
B
C
D
11.某公园计划在一块长方形草坪上修两条人行横道,修建方案如图所示,求剩余草坪的面积.
反馈练习:
(7–2)×(4–1)=15m2
12.如下图中,有一块长为32m,宽24m的长方形的草坪,其中有两条宽2m的直道把草坪分为四块,则草坪的面积是多少?
反馈练习:
(32-2)×(24-2)=660m2
13.如图,在一块长为20m,宽为8m的长方形的草地上,有一条弯曲的小路(小路任何地方的水平宽度都是0.5m).请你猜想草地的面积是多少?
反馈练习:
(20–0.5)×8=156 m2
作业:完成课时作业本相应习题.
要求:字迹工整,表述科学.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
