苏科版数学七年级下册:9.5因式分解的意义,提公因式法(1) (共16张PPT)
文档属性
| 名称 | 苏科版数学七年级下册:9.5因式分解的意义,提公因式法(1) (共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 885.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 21:34:01 | ||
图片预览






文档简介
初中数学七年级下册
(苏科版)
9.5多项式的因式分解(1)
6
6
6
4.9
2.8
2.3
6×4.9+6 ×2.8+6 ×2.3
=6×(4.9+2.8+2.3)
=60
一、自主先学
6
6
6
4.9
2.8
2.3
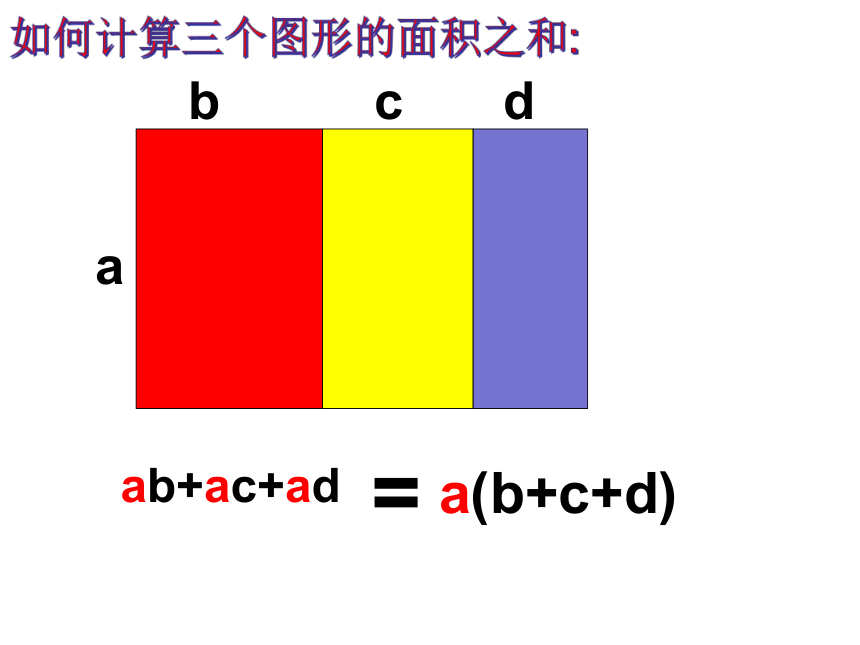
a
a
a
b
c
d
ab+ac+ad
a
b
c
d
a(b+c+d)
=
ab+ac+ad
观察多项式ab+ac+ad的每一项,你有什么发现吗?
一个多项式各项都含有的因式,称为这个多项式各项的公因式.
想一想
1、下列多项式的各项是否有公因式?如果有,
试找出公因式。
(1) 6a+8b
(2) ab-ac
(3) 2x2-6x3
(4) ab+bc-cd
a
2x2
2
思考:如何确定多项式各项的公因式?
没有
二、合作互学
(1)系数:取各项系数
的最大公约数
(2)字母:取各项相
同的字母
(3)指数:取各项相同字母
指数最低的次数
公因式确定方法:
(1)系数:取各项系数的最大公约数
(2)字母:取各项相同的字母
(3)指数:取各项相同字母指数最低的次数
练习1:找出下列多项式各项的公因式
(1)6a3b-9a2b2c
(2)-2m3+8m2-12m
3a2b
-2m
说明:当多项式的首项系数为负时,通常
把“-” 号作为公因式的符号。
(2)-2m3+8m2-12m
解:原式
=-2m .(m2-4m+6)
说明:当多项式的首项系数为负时,通常把
“-” 号作为公因式的符号进行因式分解,
使括号内首项系数为正。
.
.
.
.
.
.
=-2m m2-2m (-4m)-2m 6
.
把一个多项式写成几个整式的积的形式叫做多项式的因式分解。
练习2:下列各式由左边到右边的变形, 哪些是因
式分解,哪些不是?
(1) a2-ab=a(a-b)
(2) (a+1)(a-1) = a2-1
(3)
(4) ab+ac+d=a(b+c)+d
不是
是
不是
不是
把一个多项式写成几个整式的积的形式叫做多项式的因式分解。
练习3:把下列各式分解因式
(1)4x2 -12x3
(2)-x2y+4xy-5y
总 结
如果多项式的各项有公因式,那么就可以把这个公因式提出来,把多项式化成公因式与另一个多项式的积的形式,这种分解因式的方法叫做提公因式法.
三、检测评学
8
- 2x
2a2b
c
把 (m+n)(p+q)–(m+n)(p-q) 分解因式
四、践行活学
解:原式= (m+n)[(p+q)–(p-q)]
=(m+n)( p+q–p+q)
=2q(m+n)
四、践行活学
已知x+y=5 , xy=3 , 求x2y+xy2 的值.
这节课你有什么收获?
课堂小结
你还有什么疑惑?
中午:同步练习47页
晚上:同步练习48页
(苏科版)
9.5多项式的因式分解(1)
6
6
6
4.9
2.8
2.3
6×4.9+6 ×2.8+6 ×2.3
=6×(4.9+2.8+2.3)
=60
一、自主先学
6
6
6
4.9
2.8
2.3
a
a
a
b
c
d
ab+ac+ad
a
b
c
d
a(b+c+d)
=
ab+ac+ad
观察多项式ab+ac+ad的每一项,你有什么发现吗?
一个多项式各项都含有的因式,称为这个多项式各项的公因式.
想一想
1、下列多项式的各项是否有公因式?如果有,
试找出公因式。
(1) 6a+8b
(2) ab-ac
(3) 2x2-6x3
(4) ab+bc-cd
a
2x2
2
思考:如何确定多项式各项的公因式?
没有
二、合作互学
(1)系数:取各项系数
的最大公约数
(2)字母:取各项相
同的字母
(3)指数:取各项相同字母
指数最低的次数
公因式确定方法:
(1)系数:取各项系数的最大公约数
(2)字母:取各项相同的字母
(3)指数:取各项相同字母指数最低的次数
练习1:找出下列多项式各项的公因式
(1)6a3b-9a2b2c
(2)-2m3+8m2-12m
3a2b
-2m
说明:当多项式的首项系数为负时,通常
把“-” 号作为公因式的符号。
(2)-2m3+8m2-12m
解:原式
=-2m .(m2-4m+6)
说明:当多项式的首项系数为负时,通常把
“-” 号作为公因式的符号进行因式分解,
使括号内首项系数为正。
.
.
.
.
.
.
=-2m m2-2m (-4m)-2m 6
.
把一个多项式写成几个整式的积的形式叫做多项式的因式分解。
练习2:下列各式由左边到右边的变形, 哪些是因
式分解,哪些不是?
(1) a2-ab=a(a-b)
(2) (a+1)(a-1) = a2-1
(3)
(4) ab+ac+d=a(b+c)+d
不是
是
不是
不是
把一个多项式写成几个整式的积的形式叫做多项式的因式分解。
练习3:把下列各式分解因式
(1)4x2 -12x3
(2)-x2y+4xy-5y
总 结
如果多项式的各项有公因式,那么就可以把这个公因式提出来,把多项式化成公因式与另一个多项式的积的形式,这种分解因式的方法叫做提公因式法.
三、检测评学
8
- 2x
2a2b
c
把 (m+n)(p+q)–(m+n)(p-q) 分解因式
四、践行活学
解:原式= (m+n)[(p+q)–(p-q)]
=(m+n)( p+q–p+q)
=2q(m+n)
四、践行活学
已知x+y=5 , xy=3 , 求x2y+xy2 的值.
这节课你有什么收获?
课堂小结
你还有什么疑惑?
中午:同步练习47页
晚上:同步练习48页
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
