苏科版数学七年级下册:12.2 证明(共19张PPT)
文档属性
| 名称 | 苏科版数学七年级下册:12.2 证明(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 583.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览




文档简介
初中数学七年级下册
(苏科版)
12.2 证明(3)
180°
大家都知道:
三角形的内角和是 .
探索发现一
你有哪些途径可以验证三角形的内角和是180度呢?
探索发现一
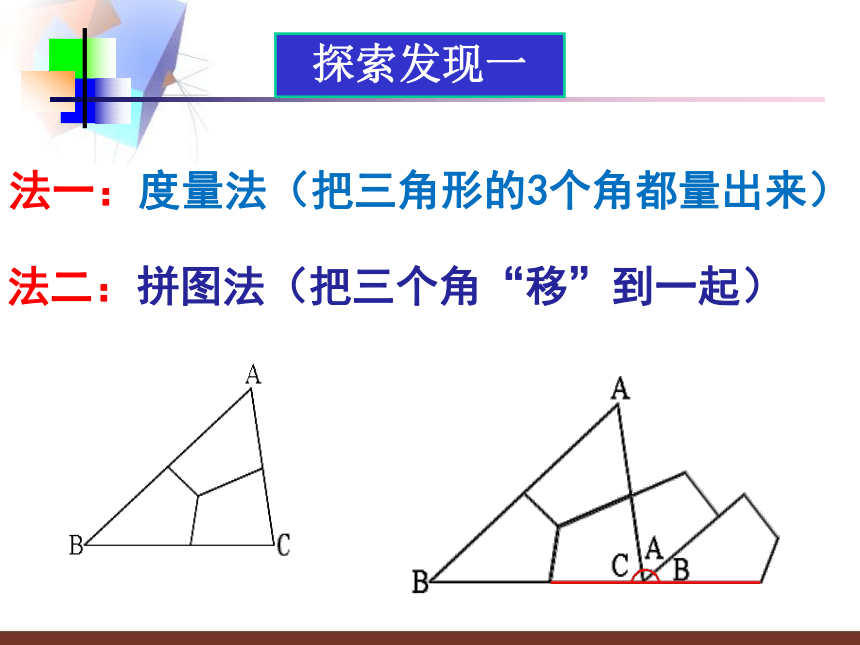
法一:度量法(把三角形的3个角都量出来)
法二:拼图法(把三个角“移”到一起)
如何通过说理的方式来证明三角形内角和等于180°?
探索发现一
A
B
C
1
2
D
E
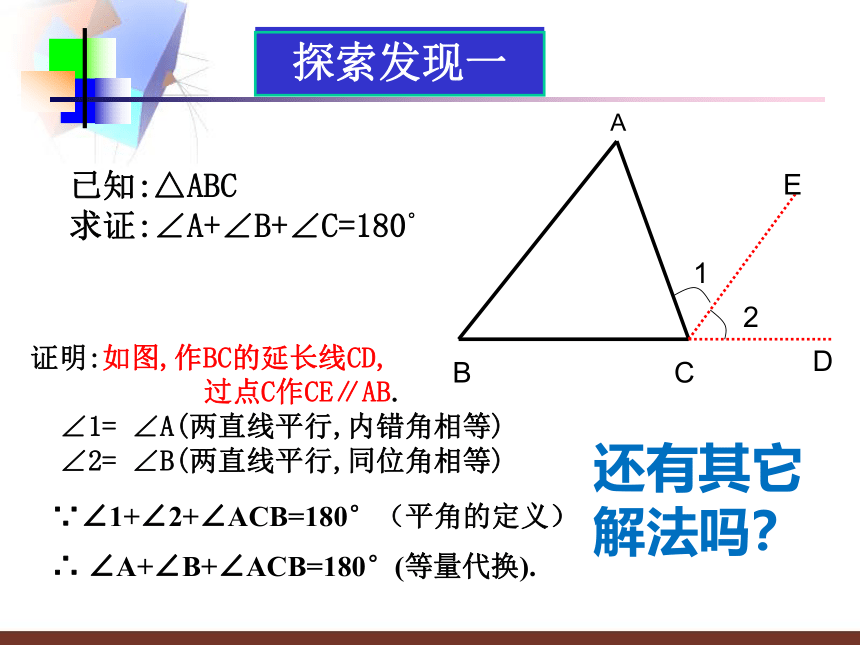
已知:△ABC
求证:∠A+∠B+∠C=180°
证明:如图,作BC的延长线CD,
过点C作CE∥AB.
∠1= ∠A(两直线平行,内错角相等)
∠2= ∠B(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°(平角的定义)
∴ ∠A+∠B+∠ACB=180°(等量代换).
探索发现
探索发现一
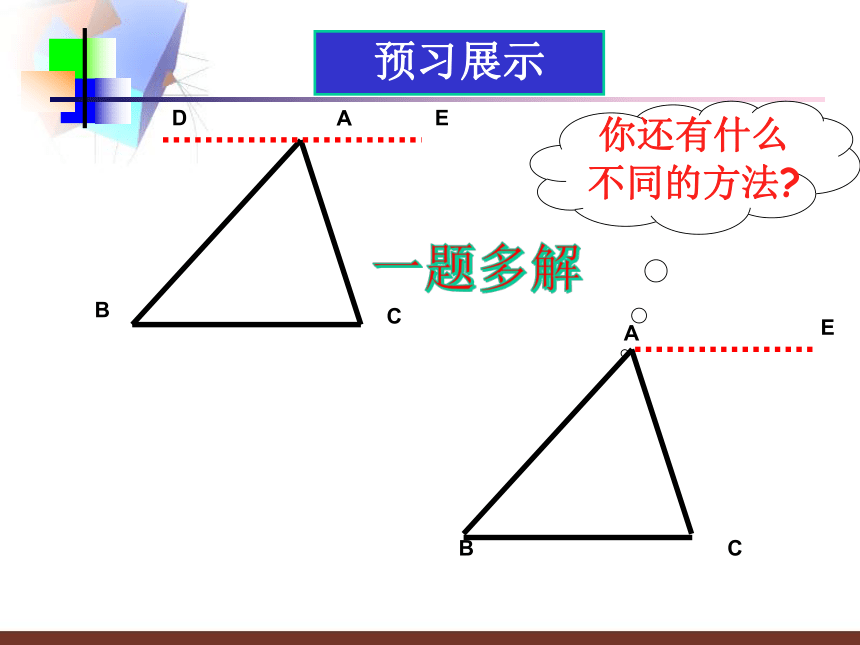
还有其它解法吗?
A
B
C
E
D
你还有什么
不同的方法?
E
B
C
A
预习展示
三角形内角和定理 :
三角形三个内角的和等于180°。
归纳总结
方法总结: 为了说明三个角的和为1800,转化为一个平角或两直线平行,同旁内角互补,体现了数学中的转化思想;
例题教学:
已知:如图,AC、BD相交于点O.
求证:∠A+∠B=∠C+∠D.
在△AOB中,
∠A+∠B+∠AOB= 180o (三角形的内角和等于180o ).
∴∠A+∠B =180°-∠AOB(等式性质).
在△COD中,同理得:∠C+∠D =180°-∠COD.
∵∠AOB=∠COD(对顶角相等).
∴∠A+∠B=∠C+∠D(等量代换).
证明:
B
A
C
D
O
变式训练
A
B
C
D
O
E
求∠A+∠B+∠C+∠D+∠E的度数.
1
(
2
(
已知:如图,AC、BD相交于点O,
求证:∠A+∠B=∠C+∠D.
例题
如图,∠α是△ABC的一个外角,∠α与△ABC的内角有怎样的大小关系?
由三角形内角和定理,可以知道:∠α=∠A+∠B
三角形内角和定理的推论:
三角形的一个外角等于和它不相邻的两个内角的和;
(由一个定理直接推出的正确结论,叫做这个定理的推论,它可以作为证明的依据。)
α
C
B
A
γ
β
探索发现二
例题教学:
已知:如图,AC、BD相交于点O.
求证:∠A+∠B=∠C+∠D.
B
A
C
D
O
你还有其它解法吗?
1.如图,探究∠BDC 与∠A 、∠B、 ∠C之间的数量关系?证明你的结论.
你有几种证明的方法呢?
2、如图,在五角星中,∠A+∠B+∠C+∠D+∠E=____
A
E
D
C
B
M
N
随堂练习
如图,∠1+∠2+∠3+∠4+∠5+∠6=____
已知:如图,AD是△ABC的角平分线,E是BC
求证:∠ADE=∠DAE.
课本P154“练一练”
相信你能行!
延长线上一点,∠EAC=∠B.
(
(
(
(
1
2
随堂练习
畅谈收获,反思升华:
通过今天的学习,你有何收获和体会.把你的收获告诉你的同学。
1.我们通过添加辅助线,把三角形的3个内角拼成1个平角;把三角形的3个内角拼成两平行线的同旁内角,证明了三角形内角和定理及推论.
4.继续感受数学的严谨、结论的确定,初步养成言之有理、落笔有据的推理习惯,发展初步的演绎推理能力.
课堂小结
2.如何证明角相等:(1)把角求出来证明度数相等;(2)把角表示出来,再证明等量关系;
3.一题多解的思维方式和转化的数学思想;
关于辅助线
1.辅助线是为了证明需要在原图上添画的
线.(辅助线通常画成虚线)
2.它的作用是把分散的条件集中,把隐含
的条件显现出来,起到牵线搭桥的作用.
3.添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题
转化,但辅助线的添法没有一定的规律,
要根据需要而定,平时做题时要注意总结.
△ABC的内角∠ABC的平分线与外角∠ACM相交于点E,请探究∠BEC与∠A的关系。
(苏科版)
12.2 证明(3)
180°
大家都知道:
三角形的内角和是 .
探索发现一
你有哪些途径可以验证三角形的内角和是180度呢?
探索发现一
法一:度量法(把三角形的3个角都量出来)
法二:拼图法(把三个角“移”到一起)
如何通过说理的方式来证明三角形内角和等于180°?
探索发现一
A
B
C
1
2
D
E
已知:△ABC
求证:∠A+∠B+∠C=180°
证明:如图,作BC的延长线CD,
过点C作CE∥AB.
∠1= ∠A(两直线平行,内错角相等)
∠2= ∠B(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°(平角的定义)
∴ ∠A+∠B+∠ACB=180°(等量代换).
探索发现
探索发现一
还有其它解法吗?
A
B
C
E
D
你还有什么
不同的方法?
E
B
C
A
预习展示
三角形内角和定理 :
三角形三个内角的和等于180°。
归纳总结
方法总结: 为了说明三个角的和为1800,转化为一个平角或两直线平行,同旁内角互补,体现了数学中的转化思想;
例题教学:
已知:如图,AC、BD相交于点O.
求证:∠A+∠B=∠C+∠D.
在△AOB中,
∠A+∠B+∠AOB= 180o (三角形的内角和等于180o ).
∴∠A+∠B =180°-∠AOB(等式性质).
在△COD中,同理得:∠C+∠D =180°-∠COD.
∵∠AOB=∠COD(对顶角相等).
∴∠A+∠B=∠C+∠D(等量代换).
证明:
B
A
C
D
O
变式训练
A
B
C
D
O
E
求∠A+∠B+∠C+∠D+∠E的度数.
1
(
2
(
已知:如图,AC、BD相交于点O,
求证:∠A+∠B=∠C+∠D.
例题
如图,∠α是△ABC的一个外角,∠α与△ABC的内角有怎样的大小关系?
由三角形内角和定理,可以知道:∠α=∠A+∠B
三角形内角和定理的推论:
三角形的一个外角等于和它不相邻的两个内角的和;
(由一个定理直接推出的正确结论,叫做这个定理的推论,它可以作为证明的依据。)
α
C
B
A
γ
β
探索发现二
例题教学:
已知:如图,AC、BD相交于点O.
求证:∠A+∠B=∠C+∠D.
B
A
C
D
O
你还有其它解法吗?
1.如图,探究∠BDC 与∠A 、∠B、 ∠C之间的数量关系?证明你的结论.
你有几种证明的方法呢?
2、如图,在五角星中,∠A+∠B+∠C+∠D+∠E=____
A
E
D
C
B
M
N
随堂练习
如图,∠1+∠2+∠3+∠4+∠5+∠6=____
已知:如图,AD是△ABC的角平分线,E是BC
求证:∠ADE=∠DAE.
课本P154“练一练”
相信你能行!
延长线上一点,∠EAC=∠B.
(
(
(
(
1
2
随堂练习
畅谈收获,反思升华:
通过今天的学习,你有何收获和体会.把你的收获告诉你的同学。
1.我们通过添加辅助线,把三角形的3个内角拼成1个平角;把三角形的3个内角拼成两平行线的同旁内角,证明了三角形内角和定理及推论.
4.继续感受数学的严谨、结论的确定,初步养成言之有理、落笔有据的推理习惯,发展初步的演绎推理能力.
课堂小结
2.如何证明角相等:(1)把角求出来证明度数相等;(2)把角表示出来,再证明等量关系;
3.一题多解的思维方式和转化的数学思想;
关于辅助线
1.辅助线是为了证明需要在原图上添画的
线.(辅助线通常画成虚线)
2.它的作用是把分散的条件集中,把隐含
的条件显现出来,起到牵线搭桥的作用.
3.添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题
转化,但辅助线的添法没有一定的规律,
要根据需要而定,平时做题时要注意总结.
△ABC的内角∠ABC的平分线与外角∠ACM相交于点E,请探究∠BEC与∠A的关系。
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
