苏科版数学七年级下册:第九章 整式与因式分解复习 (共17张PPT)
文档属性
| 名称 | 苏科版数学七年级下册:第九章 整式与因式分解复习 (共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 443.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 22:09:48 | ||
图片预览




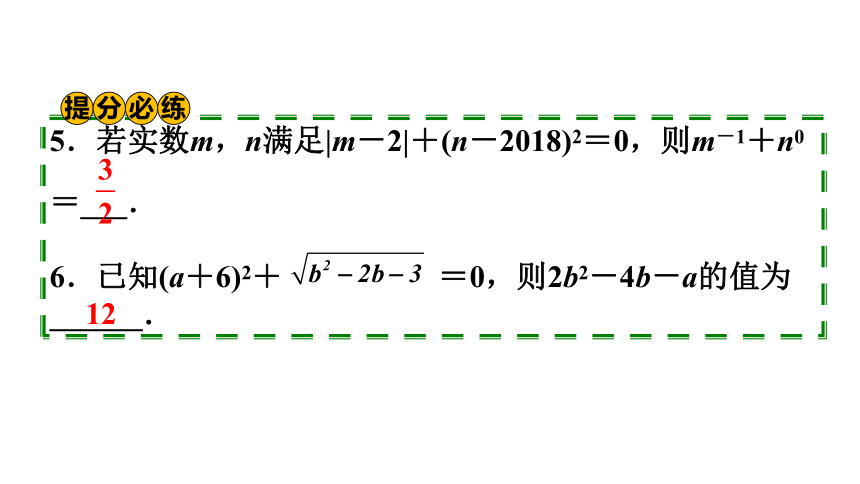

文档简介
整式与因式分解
1.列代数式
(1)原数a增加(减少)10%为①___________;比原数a的n倍多(少)m为②_______;
(2)原价a的8折为80%a;原价a按成本价提高x%后再打7.5折为③________________;
基础点 1
代数式及其求值(掌握)
基础点巧练妙记
a(1±10%)
an±m
a(1+x%)×75%
(3)x个单价为a元的商品与y个单价为b元的商品总价为④_______元;
(4)每天完成的工作量为a,则要完成m的工作量所需时间为⑤______.
(5)某商店售出一件商品的利润为a元,利润率为20%,则此商品的进价为⑥________.
ax+by
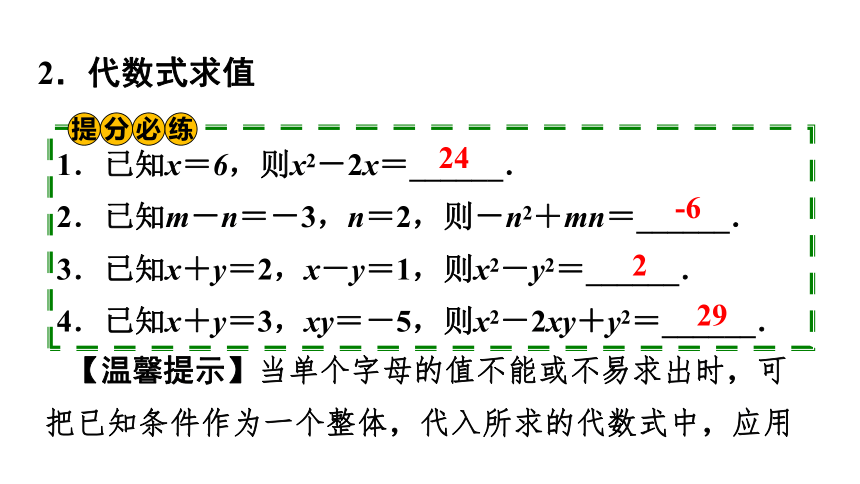
2.代数式求值
1.已知x=6,则x2-2x=______.
2.已知m-n=-3,n=2,则-n2+mn=______.
3.已知x+y=2,x-y=1,则x2-y2=______.
4.已知x+y=3,xy=-5,则x2-2xy+y2=______.
练
提
分
必
24
-6
2
29
【温馨提示】当单个字母的值不能或不易求出时,可把已知条件作为一个整体,代入所求的代数式中,应用
这种方法时先要对已知条件或者所求代数式进行变形,如找倍数关系、因式分解、移项、配方等.
3.非负数
(1)常见的非负数有 (a≥0),|a|,a2;
(2)若几个非负数的和为0,则每个非负数的值都为0,如:a2+|b|+ =0,则a2=0,|b|=0, =0.
5.若实数m,n满足|m-2|+(n-2018)2=0,则m-1+n0
=___.
6.已知(a+6)2+ =0,则2b2-4b-a的值为______.
练
提
分
必
12
1.整式的相关概念
(1)单项式:由数与字母的⑦______组成的代数式.单独的一个数或一个字母也是单项式;
(2)单项式的系数:单项式中与字母相乘的数;
(3)单项式的次数:单项式中⑧____________________;
(4)多项式:由几个单项式的和组成的代数式;
(5)多项式的次数:多项式中次数⑨______项的次数,
积
所有字母的指数的和
最高
基础点 2
整式及其计算
如:多项式3x2y2+2xy-1的次数是⑩__;
4
(6)整式:单项式和多项式统称为整式;
(7)同类项:含有的字母相同,并且相同字母的?______也分别相同.几个常数项也是同类项.
指数
7.单项式-4ab2的系数是________.
8.若2ambn和-3a3bcp是同类项,则m=________,
n=______,p=______.
练
提
分
必
-4
3
1
0
2.整式的加减运算
(1)合并同类项:合并同类项时,把?______相加,所含字母和字母的指数不变;
(2)运算法则:如有括号,先去括号再合并同类项;
(3)去括号法则:a+(b-c)=?____________,a-(b-c)=?________.(口诀:“-”变“+”不变)
a+b-c
系数
a-b+c
9. 下列运算正确的是__________.
①2x-3x=-1;②x2+x2=x4;③2x3+x3=3x3;④2a+3b=3ab;⑤-2ab+ba=-ab;
⑥8a+2b+(-5a+b)=3a+3b;⑦(ab-3b)-3(a2-b)=ab-3a2.
练
提
分
必
③⑤⑥⑦
2.幂的运算
名称
运算法则
公式表示
同底数幂的乘法
底数不变,指数相加
am·an=am+n
同底数幂的除法
底数不变,指数相减
am÷an=?____(a≠0)
幂的乘方
底数不变,指数相乘
(am)n=amn
幂的积方
各因式分别乘方的积
(ambn)p=ampbnp
am-n
4.整式的乘法运算
单项式乘以单项式
把系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.如3ab·2a=?______
单项式乘以多项式
用单项式分别去乘以多项式的每一项,再把所得的积相加减.即m(a+b+c)=?______________
6a2b
ma+mb+mc
多项式乘以多项式
用一个多项式的每一个项分别乘以另一个多项式的每一项,再把所得的积相加减
乘法公式
平方差公式:(a+b)(a-b)=?________;
完全平方公式:(a±b)2=a2±2ab+b2
a2-b2
10.下列运算正确的是_____________.
练
提
分
必
④⑤⑦⑧?
①2a+3b=5ab ②a3+a2=a5
③-2(a+b)=-2a+2b ④a3·a4=a7
⑤a3·2a4=2a7 ⑥x6÷x2=x3
⑦(x2)3=x6 ⑧(x2y)3=x6y3
⑨(-2x2y)3=-8x6y6 ⑩(x+y)2=x2+y2
?x2-y2=(x+y)(x-y)
练
提
分
必
11.化简:x(x+1)-(x-1)(x+2).
12.已知x+y=5,xy=6,求(x-4)(y-4)的值.
练
提
分
必
基础点 3
因式分解
因式分解的对象是多项式,目标是把这个多项式表示成若干个整式的乘积的形式.
若多项式各项有公因式,则先提取公因式,若无公因
式或提取公因式后,所剩项为三项,可考虑用完全平方公式;若为两项且符号相反,则可考虑用平方差公式。
13.分解因式:
(1)6x2-9x=____________;
(2)4x2-y2=____________;
(3)x3-xy2=____________;
练
提
分
必
x(x+y)(x-y)
(x-2)2
b(a-3)2
(4)x2-4x+4=___________;
(5)a2b-6ab+9b=____________.
练
提
分
必
【温馨提示】因式分解与整式的乘法运算是互逆运算,可以用整式的乘法运算验证因式分解的正误.
(x-2)2
b(a-3)2
1.列代数式
(1)原数a增加(减少)10%为①___________;比原数a的n倍多(少)m为②_______;
(2)原价a的8折为80%a;原价a按成本价提高x%后再打7.5折为③________________;
基础点 1
代数式及其求值(掌握)
基础点巧练妙记
a(1±10%)
an±m
a(1+x%)×75%
(3)x个单价为a元的商品与y个单价为b元的商品总价为④_______元;
(4)每天完成的工作量为a,则要完成m的工作量所需时间为⑤______.
(5)某商店售出一件商品的利润为a元,利润率为20%,则此商品的进价为⑥________.
ax+by
2.代数式求值
1.已知x=6,则x2-2x=______.
2.已知m-n=-3,n=2,则-n2+mn=______.
3.已知x+y=2,x-y=1,则x2-y2=______.
4.已知x+y=3,xy=-5,则x2-2xy+y2=______.
练
提
分
必
24
-6
2
29
【温馨提示】当单个字母的值不能或不易求出时,可把已知条件作为一个整体,代入所求的代数式中,应用
这种方法时先要对已知条件或者所求代数式进行变形,如找倍数关系、因式分解、移项、配方等.
3.非负数
(1)常见的非负数有 (a≥0),|a|,a2;
(2)若几个非负数的和为0,则每个非负数的值都为0,如:a2+|b|+ =0,则a2=0,|b|=0, =0.
5.若实数m,n满足|m-2|+(n-2018)2=0,则m-1+n0
=___.
6.已知(a+6)2+ =0,则2b2-4b-a的值为______.
练
提
分
必
12
1.整式的相关概念
(1)单项式:由数与字母的⑦______组成的代数式.单独的一个数或一个字母也是单项式;
(2)单项式的系数:单项式中与字母相乘的数;
(3)单项式的次数:单项式中⑧____________________;
(4)多项式:由几个单项式的和组成的代数式;
(5)多项式的次数:多项式中次数⑨______项的次数,
积
所有字母的指数的和
最高
基础点 2
整式及其计算
如:多项式3x2y2+2xy-1的次数是⑩__;
4
(6)整式:单项式和多项式统称为整式;
(7)同类项:含有的字母相同,并且相同字母的?______也分别相同.几个常数项也是同类项.
指数
7.单项式-4ab2的系数是________.
8.若2ambn和-3a3bcp是同类项,则m=________,
n=______,p=______.
练
提
分
必
-4
3
1
0
2.整式的加减运算
(1)合并同类项:合并同类项时,把?______相加,所含字母和字母的指数不变;
(2)运算法则:如有括号,先去括号再合并同类项;
(3)去括号法则:a+(b-c)=?____________,a-(b-c)=?________.(口诀:“-”变“+”不变)
a+b-c
系数
a-b+c
9. 下列运算正确的是__________.
①2x-3x=-1;②x2+x2=x4;③2x3+x3=3x3;④2a+3b=3ab;⑤-2ab+ba=-ab;
⑥8a+2b+(-5a+b)=3a+3b;⑦(ab-3b)-3(a2-b)=ab-3a2.
练
提
分
必
③⑤⑥⑦
2.幂的运算
名称
运算法则
公式表示
同底数幂的乘法
底数不变,指数相加
am·an=am+n
同底数幂的除法
底数不变,指数相减
am÷an=?____(a≠0)
幂的乘方
底数不变,指数相乘
(am)n=amn
幂的积方
各因式分别乘方的积
(ambn)p=ampbnp
am-n
4.整式的乘法运算
单项式乘以单项式
把系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.如3ab·2a=?______
单项式乘以多项式
用单项式分别去乘以多项式的每一项,再把所得的积相加减.即m(a+b+c)=?______________
6a2b
ma+mb+mc
多项式乘以多项式
用一个多项式的每一个项分别乘以另一个多项式的每一项,再把所得的积相加减
乘法公式
平方差公式:(a+b)(a-b)=?________;
完全平方公式:(a±b)2=a2±2ab+b2
a2-b2
10.下列运算正确的是_____________.
练
提
分
必
④⑤⑦⑧?
①2a+3b=5ab ②a3+a2=a5
③-2(a+b)=-2a+2b ④a3·a4=a7
⑤a3·2a4=2a7 ⑥x6÷x2=x3
⑦(x2)3=x6 ⑧(x2y)3=x6y3
⑨(-2x2y)3=-8x6y6 ⑩(x+y)2=x2+y2
?x2-y2=(x+y)(x-y)
练
提
分
必
11.化简:x(x+1)-(x-1)(x+2).
12.已知x+y=5,xy=6,求(x-4)(y-4)的值.
练
提
分
必
基础点 3
因式分解
因式分解的对象是多项式,目标是把这个多项式表示成若干个整式的乘积的形式.
若多项式各项有公因式,则先提取公因式,若无公因
式或提取公因式后,所剩项为三项,可考虑用完全平方公式;若为两项且符号相反,则可考虑用平方差公式。
13.分解因式:
(1)6x2-9x=____________;
(2)4x2-y2=____________;
(3)x3-xy2=____________;
练
提
分
必
x(x+y)(x-y)
(x-2)2
b(a-3)2
(4)x2-4x+4=___________;
(5)a2b-6ab+9b=____________.
练
提
分
必
【温馨提示】因式分解与整式的乘法运算是互逆运算,可以用整式的乘法运算验证因式分解的正误.
(x-2)2
b(a-3)2
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
