苏科版数学七年级下册9.5多项式的因式分解(1)——提公因式法课件 (共23张PPT)
文档属性
| 名称 | 苏科版数学七年级下册9.5多项式的因式分解(1)——提公因式法课件 (共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 213.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 00:00:00 | ||
图片预览








文档简介
苏科版七年级下册
第9章 整式乘法与因式分解
9.5 多项式的因式分解(1)
——提公因式法
七年级数学
七年级数学
环节一 情境创设
一块场地由三个矩形组成,这些矩形的长分别为2.8m,5m,2.2m,宽都是37m,求这块场地的面积.
2.8×37+5×37+2.2×37
(2.8+5+2.2)×37
七年级数学
环节二 探索新知
你能把多项式 ab+ac+ad 写成积的形式吗?
请说明你的理由.
根据乘法分配律:
ab+ac+ad=a(b+c+d)
我们学习了单项式乘多项式的法则
ab+ac+ad=a(b+c+d)
还有其它方法说明吗?
a(b+c+d)=ab+ac+ad
上述法则反过来,就得到
七年级数学
观察多项式 ab+ac+ad 的每一项,你有什么发现?
a 是多项式ab+ac+ad各项都含有的因式.
一个多项式各项都含有的因式,称为这个多项式各项的公因式.
环节二 探索新知
七年级数学
?
?
?
环节二 探索新知
2a叫做2a3b、4ab、8a3的公因式
????????
?
????????
?
????????
?
七年级数学
环节二 探索新知
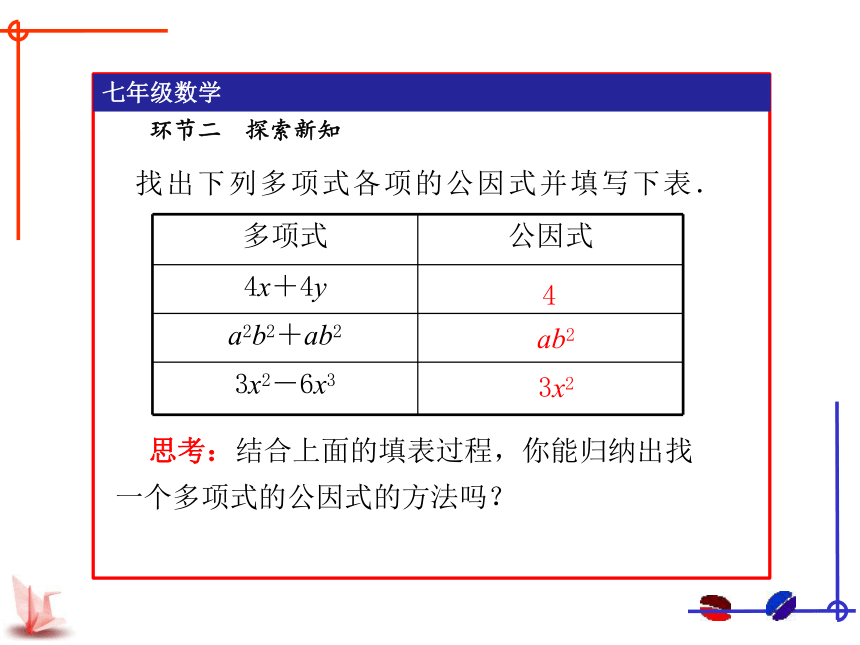
找出下列多项式各项的公因式并填写下表.
多项式
公因式
4x+4y
a2b2+ab2
3x2-6x3
思考:结合上面的填表过程,你能归纳出找一个多项式的公因式的方法吗?
4
ab2
3x2
七年级数学
找一个多项式的公因式的方法一般分三个步骤:
二看字母:
三看指数:
一看系数:
相同字母的指数取次数最低的.
一个多项式各项的公因式常常不止一个,通常
当多项式的各项系数都是整数时,公因式的系数应取各项系数的最大公约数.
公因式的字母应取多项式中各项都含有的相同字母.
环节二 探索新知
七年级数学
填空并说说你的方法:
(1)a2b+ab2= (a+b)
(2)3x2-6x3= (1-2x)
(3)9abc-6a2b2+12abc2=3ab( )
像这样,把一个多项式写成几个整式的积的形式叫做多项式的因式分解.
想一想 :
ab
3x2
3c
因式分解这一概念需要注意什么?
-2ab
+4c2
环节二 探索新知
七年级数学
1.下列各式由左到右的变形哪些是因式分解,哪些不是?
(1) ab+ac+d=a(b+c)+d
(2) a2-1=(a+1)(a-1)
(3) (a+1)(a-1)=a2-1
(4) x2-5=x(x- )
环节二 探索新知
不是
是
不是
不是
七年级数学
2.连一连:把下面左右两列具有相等关系的式子用线连起来.
4a2b(a-2b) x2-2xy+y2
(x-y)2 m2-n2
(m-n)(m+n) 4a3b-8a2b2
观察上面从左到右与从右到左的变形过程,你能说出因式分解和整式乘法的区别和联系吗?
环节二 探索新知
七年级数学
整式的乘法
积的运算
和的运算
积的运算
和的运算
整式的乘法与因式分解互为逆运算,两者的关系如下:
因式分解
一个多项式
因式分解
整式的乘法
几个整式的积
环节二 探索新知 知识积累
例1:把下列各式分解因式.
(1) 5x3-10x2
解:原式 =5x2?x-5x2?2
=5x2(x-2)
(2) 12ab2c-6ab
解:原式 =6ab?2bc-6ab?1
=6ab(2bc-1)
注意:1.如果提出的公因式与多项式中的某一项相同,那么提取后多项式中的这一项剩下“1”结果中的“1”不能漏写;
2.多项式有几项,提出公因式后另一项也有几项.
七年级数学
环节三 例题导学 新知运用
如果多项式的各项含有公因式,那么就可以把这个公因式提出来. 把多项式化成公因式与另一个多项式的积的形式,这种分解因式的方法叫做提公因式法.
七年级数学
把-2m3+8m2-12m分解因式
解:原式 =-2m?m2
分析:当多项式的第一项系数为负数时,通常把“-”作为公因式的负号写在括号外,使括号内第一项的系数为“+”.
例2:
=-2m(m2-4m+6)
环节三 例题导学 知识积累
注意点:①若首项系数为负时,一般要提出“-”号;
②不能漏项;
③是否分解到最后结果。
-2m
-2m?(-4m)
-2m?6
七年级数学
(2)分解-4x3+8x2+16x的结果是( ) A. - x(4x2-8x+16) B. x(-4x2+8x-16)
C. 4(-x3+2x2-4x) D. -4x(x2-2x-4)
C
D
(1)多项式6ab2+18a2b2-12a3b2c的公因式是( ) A. 6ab2c B. ab2 C. 6ab2 D. 6a3b2c
环节四 巩固练习 新知运用
1、选择:
-4x
(x2-2x-4)
七年级数学
2、计算:
环节四 巩固练习 巧用运算
3.46×14.7+0.54×14.7-20×1.47
解:原式=3.46×14.7+0.54×14.7-2×14.7
=14.7×(3.46+0.54-2)
=14.7×2
=29.4
七年级数学
3、下列多项式可以用提公因式法分解因式吗?
解:(1)原式 =(x+y)(3a-2b)
(2)原式 =3a(x-y)+(a-b)(x-y)
=(x-y)[3a+(a-b)]
分析:多项式的公因式一般来说是一个单项式,但有时也会是一个多项式;这时只要把那个多项式看成一个整体作为原多项式的公因式即可.
环节四 巩固练习 自主探索
3、把下列各式分解因式:
=(x-y)(4a-b)
七年级数学
环节四 巩固练习 自我检测
分解因式:
解:原式=6a(b-1)2-2(b-1)3
=2(b-1)2[3a-(b-1)]
=2(b-1)2(3a-b+1)
七年级数学
环节五 学以致用 巩固方法
1、已知a+b=2,ab=3,求代数式a2b+ab2+(a+b)的值。
解:原式 =ab(a+b)+(a+b)
=(a+b)(ab+1)
当a+b=2, ab=3时,
原式 =2×(3+1)=2×4=8
环节五 学以致用 巩固方法
七年级数学
2、从一块直径为(a+b)的圆形钢板上截出直径分别为a和b的两个圆,求出剩余钢板的面积.
a
b
解:由图得
七年级数学
环节六 拓展延伸 有效巩固
599
599
599
599
599
七年级数学
环节七 课堂小结 加深印象
通过这节课的学习,我学到了:
1、什么是公因式?
2、怎样找公因式?一般分为哪几步?
3、什么是因式分解?因式分解与整式乘法有什 么关系?
4、本节课我们学习了哪种因式分解的方法?
5、你会运用因式分解解决相关问题吗?
七年级数学
环节八 课后作业
1.完成本课补充习题
2.课后思考题(选做)
再 见!
第9章 整式乘法与因式分解
9.5 多项式的因式分解(1)
——提公因式法
七年级数学
七年级数学
环节一 情境创设
一块场地由三个矩形组成,这些矩形的长分别为2.8m,5m,2.2m,宽都是37m,求这块场地的面积.
2.8×37+5×37+2.2×37
(2.8+5+2.2)×37
七年级数学
环节二 探索新知
你能把多项式 ab+ac+ad 写成积的形式吗?
请说明你的理由.
根据乘法分配律:
ab+ac+ad=a(b+c+d)
我们学习了单项式乘多项式的法则
ab+ac+ad=a(b+c+d)
还有其它方法说明吗?
a(b+c+d)=ab+ac+ad
上述法则反过来,就得到
七年级数学
观察多项式 ab+ac+ad 的每一项,你有什么发现?
a 是多项式ab+ac+ad各项都含有的因式.
一个多项式各项都含有的因式,称为这个多项式各项的公因式.
环节二 探索新知
七年级数学
?
?
?
环节二 探索新知
2a叫做2a3b、4ab、8a3的公因式
????????
?
????????
?
????????
?
七年级数学
环节二 探索新知
找出下列多项式各项的公因式并填写下表.
多项式
公因式
4x+4y
a2b2+ab2
3x2-6x3
思考:结合上面的填表过程,你能归纳出找一个多项式的公因式的方法吗?
4
ab2
3x2
七年级数学
找一个多项式的公因式的方法一般分三个步骤:
二看字母:
三看指数:
一看系数:
相同字母的指数取次数最低的.
一个多项式各项的公因式常常不止一个,通常
当多项式的各项系数都是整数时,公因式的系数应取各项系数的最大公约数.
公因式的字母应取多项式中各项都含有的相同字母.
环节二 探索新知
七年级数学
填空并说说你的方法:
(1)a2b+ab2= (a+b)
(2)3x2-6x3= (1-2x)
(3)9abc-6a2b2+12abc2=3ab( )
像这样,把一个多项式写成几个整式的积的形式叫做多项式的因式分解.
想一想 :
ab
3x2
3c
因式分解这一概念需要注意什么?
-2ab
+4c2
环节二 探索新知
七年级数学
1.下列各式由左到右的变形哪些是因式分解,哪些不是?
(1) ab+ac+d=a(b+c)+d
(2) a2-1=(a+1)(a-1)
(3) (a+1)(a-1)=a2-1
(4) x2-5=x(x- )
环节二 探索新知
不是
是
不是
不是
七年级数学
2.连一连:把下面左右两列具有相等关系的式子用线连起来.
4a2b(a-2b) x2-2xy+y2
(x-y)2 m2-n2
(m-n)(m+n) 4a3b-8a2b2
观察上面从左到右与从右到左的变形过程,你能说出因式分解和整式乘法的区别和联系吗?
环节二 探索新知
七年级数学
整式的乘法
积的运算
和的运算
积的运算
和的运算
整式的乘法与因式分解互为逆运算,两者的关系如下:
因式分解
一个多项式
因式分解
整式的乘法
几个整式的积
环节二 探索新知 知识积累
例1:把下列各式分解因式.
(1) 5x3-10x2
解:原式 =5x2?x-5x2?2
=5x2(x-2)
(2) 12ab2c-6ab
解:原式 =6ab?2bc-6ab?1
=6ab(2bc-1)
注意:1.如果提出的公因式与多项式中的某一项相同,那么提取后多项式中的这一项剩下“1”结果中的“1”不能漏写;
2.多项式有几项,提出公因式后另一项也有几项.
七年级数学
环节三 例题导学 新知运用
如果多项式的各项含有公因式,那么就可以把这个公因式提出来. 把多项式化成公因式与另一个多项式的积的形式,这种分解因式的方法叫做提公因式法.
七年级数学
把-2m3+8m2-12m分解因式
解:原式 =-2m?m2
分析:当多项式的第一项系数为负数时,通常把“-”作为公因式的负号写在括号外,使括号内第一项的系数为“+”.
例2:
=-2m(m2-4m+6)
环节三 例题导学 知识积累
注意点:①若首项系数为负时,一般要提出“-”号;
②不能漏项;
③是否分解到最后结果。
-2m
-2m?(-4m)
-2m?6
七年级数学
(2)分解-4x3+8x2+16x的结果是( ) A. - x(4x2-8x+16) B. x(-4x2+8x-16)
C. 4(-x3+2x2-4x) D. -4x(x2-2x-4)
C
D
(1)多项式6ab2+18a2b2-12a3b2c的公因式是( ) A. 6ab2c B. ab2 C. 6ab2 D. 6a3b2c
环节四 巩固练习 新知运用
1、选择:
-4x
(x2-2x-4)
七年级数学
2、计算:
环节四 巩固练习 巧用运算
3.46×14.7+0.54×14.7-20×1.47
解:原式=3.46×14.7+0.54×14.7-2×14.7
=14.7×(3.46+0.54-2)
=14.7×2
=29.4
七年级数学
3、下列多项式可以用提公因式法分解因式吗?
解:(1)原式 =(x+y)(3a-2b)
(2)原式 =3a(x-y)+(a-b)(x-y)
=(x-y)[3a+(a-b)]
分析:多项式的公因式一般来说是一个单项式,但有时也会是一个多项式;这时只要把那个多项式看成一个整体作为原多项式的公因式即可.
环节四 巩固练习 自主探索
3、把下列各式分解因式:
=(x-y)(4a-b)
七年级数学
环节四 巩固练习 自我检测
分解因式:
解:原式=6a(b-1)2-2(b-1)3
=2(b-1)2[3a-(b-1)]
=2(b-1)2(3a-b+1)
七年级数学
环节五 学以致用 巩固方法
1、已知a+b=2,ab=3,求代数式a2b+ab2+(a+b)的值。
解:原式 =ab(a+b)+(a+b)
=(a+b)(ab+1)
当a+b=2, ab=3时,
原式 =2×(3+1)=2×4=8
环节五 学以致用 巩固方法
七年级数学
2、从一块直径为(a+b)的圆形钢板上截出直径分别为a和b的两个圆,求出剩余钢板的面积.
a
b
解:由图得
七年级数学
环节六 拓展延伸 有效巩固
599
599
599
599
599
七年级数学
环节七 课堂小结 加深印象
通过这节课的学习,我学到了:
1、什么是公因式?
2、怎样找公因式?一般分为哪几步?
3、什么是因式分解?因式分解与整式乘法有什 么关系?
4、本节课我们学习了哪种因式分解的方法?
5、你会运用因式分解解决相关问题吗?
七年级数学
环节八 课后作业
1.完成本课补充习题
2.课后思考题(选做)
再 见!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
