苏科版数学七年级下册11.5用一元一次不等式解决问题(共22张PPT)
文档属性
| 名称 | 苏科版数学七年级下册11.5用一元一次不等式解决问题(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 21:55:55 | ||
图片预览







文档简介
11.5 用一元一次不等式解决问题
1. 不等式的性质
知识回顾:
2. 解一元一次不等式的一般步骤.
3. 列方程解应用题的一般步骤.
不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变
去分母、去括号、移项、合并同类项、(含未知数项的)系数化为1.
审、设、找、列、解、验、答
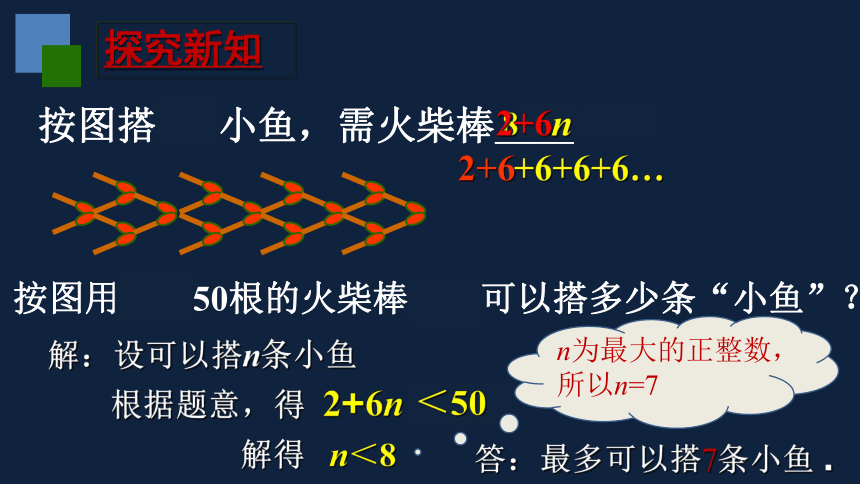
按图搭n条小鱼,需火柴棒____
8+6+6+6…
2+6+6+6+6…
2+6n
探究新知
按图用少于50根的火柴棒最多可以搭多少条“小鱼”?
解:设可以搭n条小鱼
根据题意,得
2+6n =50
<50
解得 n<8
答:最多可以搭7条小鱼 .
n为最大的正整数,
所以n=7
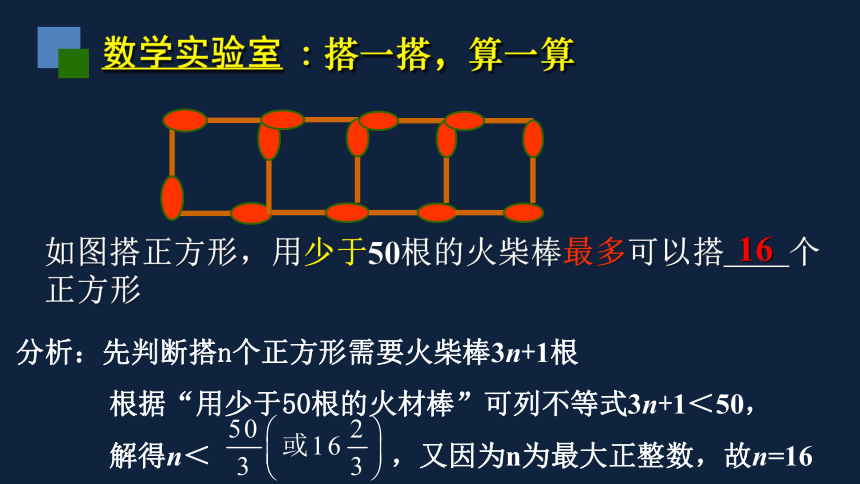
数学实验室 : 搭一搭,算一算
如图搭正方形,用少于50根的火柴棒最多可以搭____个
正方形
分析:先判断搭n个正方形需要火柴棒3n+1根
根据“用少于50根的火材棒”可列不等式3n+1<50,
解得n< ,又因为n为最大正整数,故n=16
16
归纳
用一元一次不等式解决问题一般步骤
1. 审:认真审题,分清已知量、未知量及其关系,找出题目中的
不等关系,抓住题目中的关键词,如“大于”“最多”等
2. 设:设出适当的未知数
3. 列:根据题目中的不等关系,列出不等式
4. 解:解出一元一次不等式的解集
5. 答:检验求得的解或解集是否符合实际意义,并写出答案
注意:
设不写“最多”“至少…”.
例1. 一只纸箱质量为1 kg,当放入一些苹果(每个苹果的质量 为0.25 kg)后,箱子和苹果的总质量不超过10 kg.这只纸 箱内最多能装多少个苹果?
解:设这只纸箱能装x个苹果
根据题意,得 1+0.25x≤10
设未知数时,表示不等关系的文字(如“至少”“最多”等)不能出现,否则列出来的式子应是等式,而不是不等式. 如例1中若设为“这只纸箱最多能装x个苹果”,则列出的是方程1+0.25x=10,不是不等式
注意:
典型例题:
由表示不等关系的文字可得不等关系式:
总质量≤10
解这个不等式,得 x≤36
答:这只纸箱内最多能装36个苹果 .
不等关系为:山坡上的气温≥17
例2.
某种杜鹃花适宜生长在平均气温为17 ℃到20 ℃之间的山区。已知某山区山脚下的平均气温为20 ℃,并且每上升100 m,气温下降0.6 ℃ ,要在该山区种植这种杜鹃花,应种在比山脚的海拔最多高多少米的山坡上?
解: 设这种杜鹃花应种在比山脚的海拔高x m的山坡上,
那么这个区域的平均气温是 ℃
根据题意,得 ≥17
解这个不等式,得 x≤500
答:这种杜鹃花应种在比山脚的海拔最多高500 m的山坡上
生活中的数学
解:设小明答对了x道题,则答错或不答有(20-x)道题
根据题意,得: 10x-5(20-x)>90
答:小明至少要答对13道题.
例3. 某次知识竞赛共有20道题,每一题答对得10分,答错或不答 都扣5分. 小明得分要超过90分,他至少要答对多少道题?
分析:根据“得分要超过90分”可得不等关系式:得分>90
解不等式,得: x>
利用不等式解决实际问题时,要注意问题中的限制条件,取解时必须使实际问题有意义,如人数,次数,物体的个数等为非负整数,长度,面积等为正数
因为x为最小正整数,则x=13
1. 现用甲、乙两种运输车将46吨救灾物资运往灾区,甲种车
每辆载重5吨,乙种车每辆载重4吨,安排车辆不超过10辆,
在每辆车都满载的情况下,甲种运输车需要安排_____ 辆.
试试一定行
2. 一次数学知识竞赛中,竞赛题共30题.规定:答对一道题
得4分,不答或答错一道题倒扣2分,若得分不低于60分者
获奖,则获奖者至少应答对______道题.
3. 某人骑一辆电动自行车,如果行驶速度增加5 km/h,那么2 h
所行驶的路程不少于原来速度2.5 h所行驶的路程.他原来行驶
的速度最大是_____ km/h.
1. 现用甲、乙两种运输车将46吨救灾物资运往灾区,甲种车
每辆载重5吨,乙种车每辆载重4吨,安排车辆不超过10辆,
在每辆车都满载的情况下,甲种运输车需要安排_____ 辆.
6
试试一定行
分析:根据“安排车辆不超过10辆”可得不等关系式:安排的车辆数≤10,故运用间接设未知数的方法,设甲种运输车运输x吨,则乙种运输车运输(46-x)吨,根据两种运输车数量不超过10辆建立不等式,求出解后,再求出甲种车运输的吨数,从而求出结论
解: 设甲种运输车运输x吨,则乙种运输车运输(46-x)吨,
根据题意,得:
解这个不等式,得: x≥30,
试试一定行
2. 一次数学知识竞赛中,竞赛题共30题.规定:答对一道题
得4分,不答或答错一道题倒扣2分,若得分不低于60分者
获奖,则获奖者至少应答对______道题.
分析:先求出答对题所得的分,再减去答错题的分,即可求出甲同学所得的分;
用答对题所得的分减去不答或答错题所扣的分数应≥60分,列出不等式进 行求解
解: 设获奖者答对x道题,则答错或不答(30-x)道题
根据题意得:4x-2(30-x)≥60
解这个不等式,得: x≥20,
20
试试一定行
3. 某人骑一辆电动自行车,如果行驶速度增加5 km/h,那么2 h
所行驶的路程不少于原来速度2.5 h所行驶的路程. 他原来行驶
的速度最大是_____ km/h.
分析:根据行驶速度增加5 km/h ,那么2 h所行驶的路程不少于以原来速度
2.5 h所行驶的路程,利用所行驶路程的不等关系列出不等式
解: 设原来速度为x km/h
根据题意得:2(x+5)≥2.5x
解不等式,得: x≤20
20
1. 现用甲、乙两种运输车将46吨救灾物资运往灾区,甲种车
每辆载重5吨,乙种车每辆载重4吨,安排车辆不超过10辆,
在每辆车都满载的情况下,甲种运输车需要安排_____ 辆.
试试一定行
2. 一次数学知识竞赛中,竞赛题共30题.规定:答对一道题
得4分,不答或答错一道题倒扣2分,若得分不低于60分者
获奖,则获奖者至少应答对______道题.
3. 某人骑一辆电动自行车,如果行驶速度增加5 km/h,那么2 h
所行驶的路程不少于原来速度2.5 h所行驶的路程.他原来行驶
的速度最大是_____ km/h.
6
20
20
例4.某电影院暑假向学生优惠开放,每张票2元.另外,每场 次还可以售出每张5元的普通票300张,如果要保持每场次 票房收入不低于2000元,那么平均每场次至少应出售学生 优惠票多少张?
典型例题:
分析:根据关键词“不低于2000元”得到不等关系“每场次票房收入≥2000”
解:设平均每场次应出售学生优惠票x张
根据题意,得: 2x+5×300≥2000
解这个不等式,得: x≥250
答:平均每场次应出售学生优惠票250张.
例5. “一方有难,八方支援”,地震后,某单位为一中学捐赠 了一批新桌椅,学校组织初一年级200名学生搬桌椅.规 定一人一次搬两把椅子,两人一次搬一张桌子,每人限搬 一次,最多可搬桌椅(一桌一椅为一套)多少套?
典型例题:
分析:设可搬桌椅x套,即桌子x张、椅子x把,则搬桌子需2x人,搬椅子 需 人,根据搬桌椅的人数不大于总人数的关系列不等式
解:设可搬桌椅x套,即桌子x张、椅子x把,则搬桌子需2x人,搬椅子需 人
根据题意,得:
解这个不等式,得: x≤80
答:最多可搬桌椅80套.
例题5中没有直接给出表示不等关系的关键词,而是把不等关系隐藏在总人数200人这个条件中,即搬桌椅的人数不大于总人数,需要同学们经过思考后发现
例6. 水果店进了某种水果1吨,进价是7元/千克.售价定为10元 千克,销售一半以后,为了尽快销完,准备打折出售.如果要 使利润不低于2000元,那么余下的水果至少按原定价的几折 出售?
典型例题:
分析:利润问题公式:每千克利润=售价-进价;利润=每千克利润×销售量
根据题中“利润不低于2000元”列不等式
解: 设余下的水果按原定价的x折出售,
根据题意,得: 500×(10-7)+500(x-7)≥2000
解这个不等式,得: x≥8
答:余下的水果按原定价的8折出售.
打折后售价为:
售价×
注意单位要统一,1吨要换算成1000千克
则打折后水果的售价为x元
例7. 水果店进了某种水果1吨,进价是7元/千克.售价定为10元 千克,销售一半以后,为了尽快销完,准备打折出售.如果要 使利润率不低于20%,那么余下的水果至少按原定价的几 折出售?
例6变一变:
解: 设余下的水果按原定价的x折出售, 则打折后水果的售价为x元
解这个不等式,得: x≥6.8
答:余下的水果按原定价的6.8折出售.
分析:根据“利润率不低于20%”可列不等式,这里利润率= ;
根据题意,得: ≥20%
拓展延伸:
某市居民用电的电价实行阶梯收费,收费标准如下表:
(1) 已知小明家四月份用电286度,缴纳电费
178.76元;五月份用电316度,缴纳电费
198.56元,请你根据以上数据,求出表
格中 a, b的值.
(2) 六月份是用电高峰期,小明计划六月份
电费支出不超过300元,那么小明家六月
份最多可用电多少度?
分析:四月份用电分成两段:286=200+86, 则四月份电费表示为:200a+86b 元
五月份用电分成两段:316=200+116,则五月份电费表示为:200a+116b 元
根据“四月缴纳电费178.76元,五月缴纳电费198.56元”得
二元一次方程组解出a、b的值
拓展延伸:
某市居民用电的电价实行阶梯收费,收费标准如下表:
(1)已知李叔小明家四月份用电286度,缴纳电费
178.76元;五月份用电316度,缴纳电费
198.56元,请你根据以上数据,求出表
格中 a, b的值.
(2) 六月份是用电高峰期,小明计划六月份
电费支出不超过300元,那么小明家六月
份最多可用电多少度?
(1)解:根据题意,得:
解得:
答:a为0.61元,b为0.66元.
拓展延伸:
某市居民用电的电价实行阶梯收费,收费标准如下表:
(1) 已知小明家四月份用电286度,缴纳电费
178.76元;五月份用电316度,缴纳电费
198.56元,请你根据以上数据,求出表
格中 a, b的值.
(2) 六月份是用电高峰期,小明计划六月份
电费支出不超过300元,那么小明家六月
份最多可用电多少度?
分析:根据“六月份电费支出不超出300元”可列不等式,但六月份的用电量是未知数,则六月份的电费不能立即用六月份的用电量来表示,则需要先判断六月份的用电量在哪一个分段范围.我们可以先计算出用电量第一段和第二段电费的最大值,与条件中电费的最大值300元比较大小,来确定用电量的所处的分段范围,再用未知数表示出用电量,列出不等式求解.
0.61
0.66
拓展延伸:
某市居民用电的电价实行阶梯收费,收费标准如下表:
(1) 已知小明家四月份用电286度,缴纳电费
178.76元;五月份用电316度,缴纳电费
198.56元,请你根据以上数据,求出表
格中 a, b的值.
(2) 六月份是用电高峰期,小明计划六月份
电费支出不超过300元,那么小明家六月
份最多可用电多少度?
0.61
0.66
分类讨论思想
(2)解:设小明家六月份用电量为x度
第一段电费最大值为:200×0.61=122元;
小明家六月份用电量为:254+0.92(x-400);
第二段电费最大值为:200×0.61+(400-200)×0.66 =254元<300元,则x>400,
根据题意,得:254+0.92(x-400)≤300
解得:x≤450
答:小明家六月份最多可用电450度
列不等式解应用题基本步骤与列方程解应用题的步骤相类似,即
①审: 认真审题,分清已知量、未知量及其关系,找出题中不等 关系,要抓住题设中的关键字眼,如“大于”、“小于”、
“不小于”、“不大于”等.
②设: 设出适当的未知数.
③列: 根据题中的不等关系,列出不等式.
④解: 解出所列不等式的解集.
⑤答: 检验求得的解或解集是否符合实际意义,并写出答案.
1、 用一元一次不等式解决问题的一般步骤
课堂小结:
2、 用一元一次不等式解决问题的关键什么?
用一元一次不等式解决问题的关键是抓住题目中的关键词,
找出题目中的不等关系 .
1. 不等式的性质
知识回顾:
2. 解一元一次不等式的一般步骤.
3. 列方程解应用题的一般步骤.
不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变
去分母、去括号、移项、合并同类项、(含未知数项的)系数化为1.
审、设、找、列、解、验、答
按图搭n条小鱼,需火柴棒____
8+6+6+6…
2+6+6+6+6…
2+6n
探究新知
按图用少于50根的火柴棒最多可以搭多少条“小鱼”?
解:设可以搭n条小鱼
根据题意,得
2+6n =50
<50
解得 n<8
答:最多可以搭7条小鱼 .
n为最大的正整数,
所以n=7
数学实验室 : 搭一搭,算一算
如图搭正方形,用少于50根的火柴棒最多可以搭____个
正方形
分析:先判断搭n个正方形需要火柴棒3n+1根
根据“用少于50根的火材棒”可列不等式3n+1<50,
解得n< ,又因为n为最大正整数,故n=16
16
归纳
用一元一次不等式解决问题一般步骤
1. 审:认真审题,分清已知量、未知量及其关系,找出题目中的
不等关系,抓住题目中的关键词,如“大于”“最多”等
2. 设:设出适当的未知数
3. 列:根据题目中的不等关系,列出不等式
4. 解:解出一元一次不等式的解集
5. 答:检验求得的解或解集是否符合实际意义,并写出答案
注意:
设不写“最多”“至少…”.
例1. 一只纸箱质量为1 kg,当放入一些苹果(每个苹果的质量 为0.25 kg)后,箱子和苹果的总质量不超过10 kg.这只纸 箱内最多能装多少个苹果?
解:设这只纸箱能装x个苹果
根据题意,得 1+0.25x≤10
设未知数时,表示不等关系的文字(如“至少”“最多”等)不能出现,否则列出来的式子应是等式,而不是不等式. 如例1中若设为“这只纸箱最多能装x个苹果”,则列出的是方程1+0.25x=10,不是不等式
注意:
典型例题:
由表示不等关系的文字可得不等关系式:
总质量≤10
解这个不等式,得 x≤36
答:这只纸箱内最多能装36个苹果 .
不等关系为:山坡上的气温≥17
例2.
某种杜鹃花适宜生长在平均气温为17 ℃到20 ℃之间的山区。已知某山区山脚下的平均气温为20 ℃,并且每上升100 m,气温下降0.6 ℃ ,要在该山区种植这种杜鹃花,应种在比山脚的海拔最多高多少米的山坡上?
解: 设这种杜鹃花应种在比山脚的海拔高x m的山坡上,
那么这个区域的平均气温是 ℃
根据题意,得 ≥17
解这个不等式,得 x≤500
答:这种杜鹃花应种在比山脚的海拔最多高500 m的山坡上
生活中的数学
解:设小明答对了x道题,则答错或不答有(20-x)道题
根据题意,得: 10x-5(20-x)>90
答:小明至少要答对13道题.
例3. 某次知识竞赛共有20道题,每一题答对得10分,答错或不答 都扣5分. 小明得分要超过90分,他至少要答对多少道题?
分析:根据“得分要超过90分”可得不等关系式:得分>90
解不等式,得: x>
利用不等式解决实际问题时,要注意问题中的限制条件,取解时必须使实际问题有意义,如人数,次数,物体的个数等为非负整数,长度,面积等为正数
因为x为最小正整数,则x=13
1. 现用甲、乙两种运输车将46吨救灾物资运往灾区,甲种车
每辆载重5吨,乙种车每辆载重4吨,安排车辆不超过10辆,
在每辆车都满载的情况下,甲种运输车需要安排_____ 辆.
试试一定行
2. 一次数学知识竞赛中,竞赛题共30题.规定:答对一道题
得4分,不答或答错一道题倒扣2分,若得分不低于60分者
获奖,则获奖者至少应答对______道题.
3. 某人骑一辆电动自行车,如果行驶速度增加5 km/h,那么2 h
所行驶的路程不少于原来速度2.5 h所行驶的路程.他原来行驶
的速度最大是_____ km/h.
1. 现用甲、乙两种运输车将46吨救灾物资运往灾区,甲种车
每辆载重5吨,乙种车每辆载重4吨,安排车辆不超过10辆,
在每辆车都满载的情况下,甲种运输车需要安排_____ 辆.
6
试试一定行
分析:根据“安排车辆不超过10辆”可得不等关系式:安排的车辆数≤10,故运用间接设未知数的方法,设甲种运输车运输x吨,则乙种运输车运输(46-x)吨,根据两种运输车数量不超过10辆建立不等式,求出解后,再求出甲种车运输的吨数,从而求出结论
解: 设甲种运输车运输x吨,则乙种运输车运输(46-x)吨,
根据题意,得:
解这个不等式,得: x≥30,
试试一定行
2. 一次数学知识竞赛中,竞赛题共30题.规定:答对一道题
得4分,不答或答错一道题倒扣2分,若得分不低于60分者
获奖,则获奖者至少应答对______道题.
分析:先求出答对题所得的分,再减去答错题的分,即可求出甲同学所得的分;
用答对题所得的分减去不答或答错题所扣的分数应≥60分,列出不等式进 行求解
解: 设获奖者答对x道题,则答错或不答(30-x)道题
根据题意得:4x-2(30-x)≥60
解这个不等式,得: x≥20,
20
试试一定行
3. 某人骑一辆电动自行车,如果行驶速度增加5 km/h,那么2 h
所行驶的路程不少于原来速度2.5 h所行驶的路程. 他原来行驶
的速度最大是_____ km/h.
分析:根据行驶速度增加5 km/h ,那么2 h所行驶的路程不少于以原来速度
2.5 h所行驶的路程,利用所行驶路程的不等关系列出不等式
解: 设原来速度为x km/h
根据题意得:2(x+5)≥2.5x
解不等式,得: x≤20
20
1. 现用甲、乙两种运输车将46吨救灾物资运往灾区,甲种车
每辆载重5吨,乙种车每辆载重4吨,安排车辆不超过10辆,
在每辆车都满载的情况下,甲种运输车需要安排_____ 辆.
试试一定行
2. 一次数学知识竞赛中,竞赛题共30题.规定:答对一道题
得4分,不答或答错一道题倒扣2分,若得分不低于60分者
获奖,则获奖者至少应答对______道题.
3. 某人骑一辆电动自行车,如果行驶速度增加5 km/h,那么2 h
所行驶的路程不少于原来速度2.5 h所行驶的路程.他原来行驶
的速度最大是_____ km/h.
6
20
20
例4.某电影院暑假向学生优惠开放,每张票2元.另外,每场 次还可以售出每张5元的普通票300张,如果要保持每场次 票房收入不低于2000元,那么平均每场次至少应出售学生 优惠票多少张?
典型例题:
分析:根据关键词“不低于2000元”得到不等关系“每场次票房收入≥2000”
解:设平均每场次应出售学生优惠票x张
根据题意,得: 2x+5×300≥2000
解这个不等式,得: x≥250
答:平均每场次应出售学生优惠票250张.
例5. “一方有难,八方支援”,地震后,某单位为一中学捐赠 了一批新桌椅,学校组织初一年级200名学生搬桌椅.规 定一人一次搬两把椅子,两人一次搬一张桌子,每人限搬 一次,最多可搬桌椅(一桌一椅为一套)多少套?
典型例题:
分析:设可搬桌椅x套,即桌子x张、椅子x把,则搬桌子需2x人,搬椅子 需 人,根据搬桌椅的人数不大于总人数的关系列不等式
解:设可搬桌椅x套,即桌子x张、椅子x把,则搬桌子需2x人,搬椅子需 人
根据题意,得:
解这个不等式,得: x≤80
答:最多可搬桌椅80套.
例题5中没有直接给出表示不等关系的关键词,而是把不等关系隐藏在总人数200人这个条件中,即搬桌椅的人数不大于总人数,需要同学们经过思考后发现
例6. 水果店进了某种水果1吨,进价是7元/千克.售价定为10元 千克,销售一半以后,为了尽快销完,准备打折出售.如果要 使利润不低于2000元,那么余下的水果至少按原定价的几折 出售?
典型例题:
分析:利润问题公式:每千克利润=售价-进价;利润=每千克利润×销售量
根据题中“利润不低于2000元”列不等式
解: 设余下的水果按原定价的x折出售,
根据题意,得: 500×(10-7)+500(x-7)≥2000
解这个不等式,得: x≥8
答:余下的水果按原定价的8折出售.
打折后售价为:
售价×
注意单位要统一,1吨要换算成1000千克
则打折后水果的售价为x元
例7. 水果店进了某种水果1吨,进价是7元/千克.售价定为10元 千克,销售一半以后,为了尽快销完,准备打折出售.如果要 使利润率不低于20%,那么余下的水果至少按原定价的几 折出售?
例6变一变:
解: 设余下的水果按原定价的x折出售, 则打折后水果的售价为x元
解这个不等式,得: x≥6.8
答:余下的水果按原定价的6.8折出售.
分析:根据“利润率不低于20%”可列不等式,这里利润率= ;
根据题意,得: ≥20%
拓展延伸:
某市居民用电的电价实行阶梯收费,收费标准如下表:
(1) 已知小明家四月份用电286度,缴纳电费
178.76元;五月份用电316度,缴纳电费
198.56元,请你根据以上数据,求出表
格中 a, b的值.
(2) 六月份是用电高峰期,小明计划六月份
电费支出不超过300元,那么小明家六月
份最多可用电多少度?
分析:四月份用电分成两段:286=200+86, 则四月份电费表示为:200a+86b 元
五月份用电分成两段:316=200+116,则五月份电费表示为:200a+116b 元
根据“四月缴纳电费178.76元,五月缴纳电费198.56元”得
二元一次方程组解出a、b的值
拓展延伸:
某市居民用电的电价实行阶梯收费,收费标准如下表:
(1)已知李叔小明家四月份用电286度,缴纳电费
178.76元;五月份用电316度,缴纳电费
198.56元,请你根据以上数据,求出表
格中 a, b的值.
(2) 六月份是用电高峰期,小明计划六月份
电费支出不超过300元,那么小明家六月
份最多可用电多少度?
(1)解:根据题意,得:
解得:
答:a为0.61元,b为0.66元.
拓展延伸:
某市居民用电的电价实行阶梯收费,收费标准如下表:
(1) 已知小明家四月份用电286度,缴纳电费
178.76元;五月份用电316度,缴纳电费
198.56元,请你根据以上数据,求出表
格中 a, b的值.
(2) 六月份是用电高峰期,小明计划六月份
电费支出不超过300元,那么小明家六月
份最多可用电多少度?
分析:根据“六月份电费支出不超出300元”可列不等式,但六月份的用电量是未知数,则六月份的电费不能立即用六月份的用电量来表示,则需要先判断六月份的用电量在哪一个分段范围.我们可以先计算出用电量第一段和第二段电费的最大值,与条件中电费的最大值300元比较大小,来确定用电量的所处的分段范围,再用未知数表示出用电量,列出不等式求解.
0.61
0.66
拓展延伸:
某市居民用电的电价实行阶梯收费,收费标准如下表:
(1) 已知小明家四月份用电286度,缴纳电费
178.76元;五月份用电316度,缴纳电费
198.56元,请你根据以上数据,求出表
格中 a, b的值.
(2) 六月份是用电高峰期,小明计划六月份
电费支出不超过300元,那么小明家六月
份最多可用电多少度?
0.61
0.66
分类讨论思想
(2)解:设小明家六月份用电量为x度
第一段电费最大值为:200×0.61=122元;
小明家六月份用电量为:254+0.92(x-400);
第二段电费最大值为:200×0.61+(400-200)×0.66 =254元<300元,则x>400,
根据题意,得:254+0.92(x-400)≤300
解得:x≤450
答:小明家六月份最多可用电450度
列不等式解应用题基本步骤与列方程解应用题的步骤相类似,即
①审: 认真审题,分清已知量、未知量及其关系,找出题中不等 关系,要抓住题设中的关键字眼,如“大于”、“小于”、
“不小于”、“不大于”等.
②设: 设出适当的未知数.
③列: 根据题中的不等关系,列出不等式.
④解: 解出所列不等式的解集.
⑤答: 检验求得的解或解集是否符合实际意义,并写出答案.
1、 用一元一次不等式解决问题的一般步骤
课堂小结:
2、 用一元一次不等式解决问题的关键什么?
用一元一次不等式解决问题的关键是抓住题目中的关键词,
找出题目中的不等关系 .
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
