苏科版数学七年级下册第十一章一元一次不等式复习(共25张PPT)
文档属性
| 名称 | 苏科版数学七年级下册第十一章一元一次不等式复习(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 21:58:26 | ||
图片预览







文档简介
第11 章 一元一次不等式复习
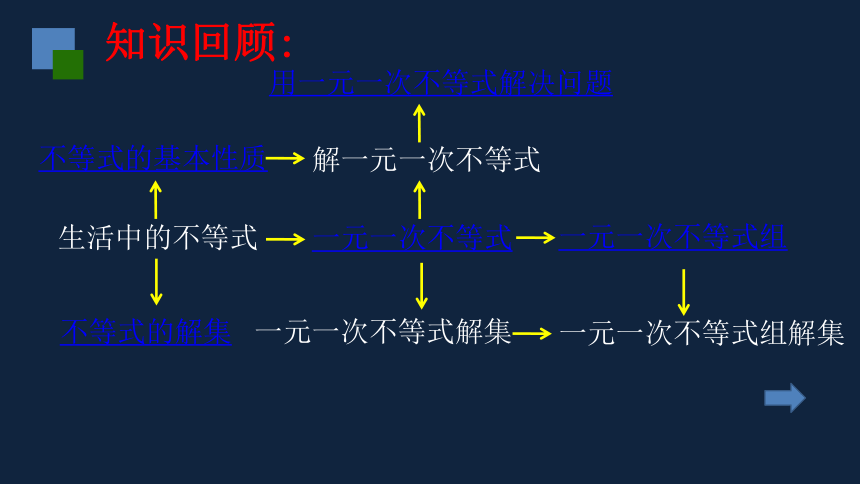
知识回顾:
生活中的不等式
不等式的基本性质
不等式的解集
用一元一次不等式解决问题
解一元一次不等式
一元一次不等式
一元一次不等式组
一元一次不等式组解集
一元一次不等式解集
不等式的解集
2.如何在数轴上表示不等式的解集?
知识回顾:
-3
-2
-1
3
1
0
2
在数轴上表示????>?2的解集
?
1.什么是不等式的解集?
能使不等式成立的未知数的值叫做不等式的解.
一个含有未知数的不等式的所有的解,组成这个不等式的解的集合,简称这个不等式的解集.
不等式的基本性质
1.不等式的基本性质1:
不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
知识回顾:
2.不等式的基本性质2:
不等式的两边都乘(或除以)同一个正数,不等号的方向不变;
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
一元一次不等式
只含有一个未知数,并且未知数的次数都是1,系数不等于0,这样的不等式叫做一元一次不等式.
知识回顾:
去分母、去括号、移项、合并同类项、(含未知数项的)系数化为1.通过这些步骤把一元一次不等式逐步转化为x>a(x≥a)或x<a(x≤a)的形式.
解一元一次不等式
用一元一次不等式解决问题的步骤:
1.认真审题,分清已知量、未知量及其关系,找出题中不等关系,要抓住题设中的关键字词,如“大于”、“小于”、“不小于”、“不大于”等的含义.
2.设出适当的未知数.
3.根据题中的不等关系,列出不等式.
4.解出所列不等式的解集.
5.写出答案,并检验答案是否符合题意.
知识回顾:
一元一次不等式组
1.定义
不等式组中所有不等式的解集的公共部分叫做不等式组的解集.
2.解一元一次不等式组先分别求出不等式组中每个不等式的解集, 再求出这几个不等式解集的公共部分.
知识回顾:
把几个含有同一个未知数的一次不等式联立在一起,就组成了一个一元一次不等式组.
不等式组解集
知识回顾:
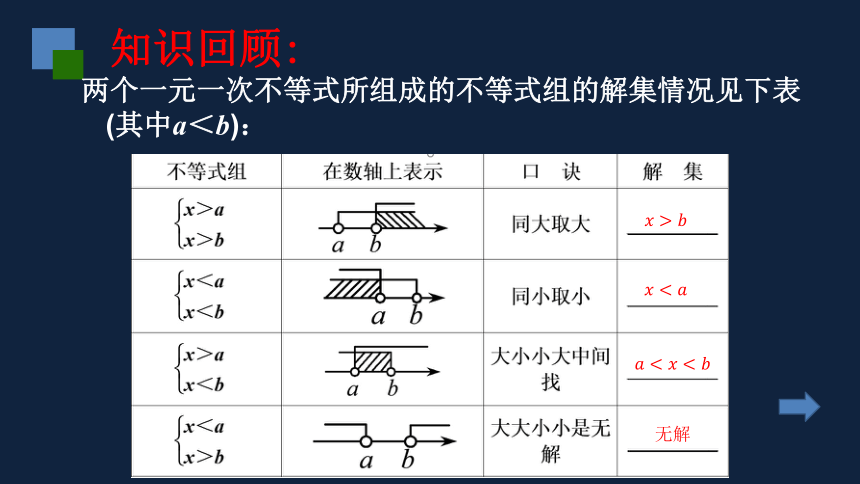
两个一元一次不等式所组成的不等式组的解集情况见下表(其中a<b):
????>????
?
?????
?????
无解
?
复习巩固
解:(1)a?1?0
?
1.用不等式表示:
(1)a与1的差是负数;
(2)x的2倍大于x的三倍与1的和
(3)代数式4x+1的值不小于2
?
(2)2x ?3x+1
(3)4x +1 ?2
复习巩固
(1)a?1?0
?
2.解不等式:
?
(2)2x ?3x+1
(3)4x +1 ?2
解:(1)a?1?0
?
a ? 1
(2) 2x ?3x+1
x ? ?1
?
(3)4x +1 ?2
4x ?1
x ?14
?
??x > 1
?
复习巩固
(1)3?????3<?????15
?
3.解下列不等式,并把它们的解集分别在数轴上表示出来
?
(2)5(x?1) <2(7x+2)
?
解:(1) 3x ??9<?????15
?
(2)?????12<7????+25
?
3x ?????<9?15
?
2????<?6
?
????<?3
?
5x?5 <14x+4
?
?9x <9
?
x >?1
?
-3
-2
-1
3
1
0
2
-5
-4
0
-2
-3
-1
4. 解下列不等式组.
复习巩固
(1)&2????+4>0,????????①&1?2????>0.????????②
?
解:(1)解不等式①,得
????<12
?
????>?2
?
解不等式②,得
不等式组的解集是
?2?
在数轴上表示出不等式组的解集
(2)&?????24>?????13,????????①&2(????+1)>????+3.????????②
?
-2
-1
1
0
12
?
4. 解下列不等式组.
复习巩固
解:(1)解不等式①,得
?????> 2
?
3?????6>4?????4
?
解不等式②,得
不等式组无解
在数轴上表示出不等式组的解集
(2)&?????24>?????13,???????????????①&2(????+1)>????+3.?②
?
?????
2????+2>????+3
?
????>1
?
3(?????2)>4(?????1)
?
-2
-1
1
0
5. 求不等式组&3?????6<4?????,???①&?????1>4?????10.?②的非负整数解.
?
复习巩固
解:解不等式①,得
解不等式②,得
4????<10
?
9>3????
?
????<2.5
?
∴不等式组的解集是
????<3
?
????<2.5
?
∴不等式组的非负整数解是:0,1,2
6.已知不等式组&????>1,???①&?????
复习巩固
不等式组无解,则
-1
1
0
2
在数轴上表示不等式① 的解集
?????1
?
????<1
?
a
变式1.已知不等式组&????>1,???①&?????
复习巩固
不等式组只有一个整数解,则整数解是 2
在数轴上表示不等式① 的解集
2?
1
0
2
3
则a的取值范围是
2?
a
7.已知关于x方程?????2?????????=2的解是正数,求a的取值范围.
?
复习巩固
解:解方程得
由题意得:x > 0
?
?????2????+????=2
?
则?????2>0
?
?????+????=2
?
????=?????2
?
????>2
?
变式1.已知关于x方程?????2?????????=2的解是负数,求正整数a的值.
?
复习巩固
解:解方程得
由题意得:x <0
?
?????2????+????=2
?
则?????2<0
?
?????+????=2
?
????=?????2
?
????<2
?
∵a是正整数
∴a的值是1
变式2.已知关于x,y方程组????+????=2????+1??①?????????=4?????3??②的解x、y是正数,求a的取值范围.
?
复习巩固
解:① +?②得:2????=6?????2
?
由题意得:x >0, y >0
?
则3?????1>0?????+2>0
?
解得 13?
????=3?????1
?
① ??②得:2????=?2????+4
?
????=?????+2
?
变式3.已知关于x,y方程组2????+????=2?3?????①????+2????=4?????????????②的解满足x+y>?2,
求满足条件的m的所有正整数的值.
?
复习巩固
解:① +?②得:3????+3????=6?3????
?
由题意得:x +?????> ?2
?
则2?????>?2
?
????<4
?
????+????=2?????
?
?????>?4
?
∴m的正整数值是1,2,3
8. 某车工计划在15天内至少加工零件408个,前三天每天加工零件24个.此后,该车工平均每天至少需要加工零件多少个,才能在规定的实际完成任务?
复习巩固
解:设以后平均每天加工零件x个
24×3+12?????408
?
根据题意可得:
?????28
?
答:该车工平均每天至少需要加工零件28个
9. 某药店出售消毒免洗手液和口罩,免洗手消毒液每瓶20元,每包口罩5元,该药店有两种优惠方法:
(1)买一瓶消毒免洗手液送一包口罩;(2)按总价的92%付款.
小明需要购买防疫物资做开学准备,需购买4瓶消毒免洗手液、若干包口罩(不少于4包),请问小明买同样多的口罩时,用哪种优惠方法购买省钱?
复习巩固
9. 某药店出售消毒免洗手液和口罩,免洗手消毒液每瓶20元,每包口罩5元,该药店有两种优惠方法:(1)买一瓶消毒免洗手液送一包口罩;(2)按总价的92%付款.
小明需要购买防疫物资做开学准备,需购买4瓶消毒免洗手液、若干包口罩(不少于4包),请问小明买同样多的口罩时,用哪种优惠方法购买省钱?
复习巩固
解:设小明需要购买x(x ? 4)包口罩,
记优惠方法(1)需要花费为y1
①????1>?????2 则5????+60>4.6????+73.6
?
????>34
?
②????1<?????2 则5????+60<4.6????+73.6
?
????<34
?
③????1=?????2?则5????+60=4.6????+73.6
?
????=34
?
答:当小明购买口罩数量大于34包时,选择优惠方式二;当小明购买口罩不少于四包,但小于34包时,选择优惠方式一;当小明买口罩数量等于34包时,两种优惠方式都可以.
4?????<34
?
分析:哪种“省钱”→
比较两种方式总价
→ 缺少口罩数量
→ 设x
y1=20×4+5?????4=5????+60
?
y2 =20×4+5????×0.92=4.6????+73.6
?
记优惠方法(2)需要花费为y2
选择优惠方式二
?
选择优惠方式一
?
两种优惠方式都可以
?
3、在实际问题中利用不等式解决问题.
2、解一元一次不等式(组).
课堂小结:
(1)不等式的性质.
(2)用数轴表示不等式的解集,借助数轴求出不等组解集.
(3)解不等式组口诀.
(4)含参数的不等式相关问题.
找、设、列、解、验、答.
数形结合、转化思想
1、一元一次不等式(组)定义.
第11章 一元一次不等式
谢 谢!
知识回顾:
生活中的不等式
不等式的基本性质
不等式的解集
用一元一次不等式解决问题
解一元一次不等式
一元一次不等式
一元一次不等式组
一元一次不等式组解集
一元一次不等式解集
不等式的解集
2.如何在数轴上表示不等式的解集?
知识回顾:
-3
-2
-1
3
1
0
2
在数轴上表示????>?2的解集
?
1.什么是不等式的解集?
能使不等式成立的未知数的值叫做不等式的解.
一个含有未知数的不等式的所有的解,组成这个不等式的解的集合,简称这个不等式的解集.
不等式的基本性质
1.不等式的基本性质1:
不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
知识回顾:
2.不等式的基本性质2:
不等式的两边都乘(或除以)同一个正数,不等号的方向不变;
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
一元一次不等式
只含有一个未知数,并且未知数的次数都是1,系数不等于0,这样的不等式叫做一元一次不等式.
知识回顾:
去分母、去括号、移项、合并同类项、(含未知数项的)系数化为1.通过这些步骤把一元一次不等式逐步转化为x>a(x≥a)或x<a(x≤a)的形式.
解一元一次不等式
用一元一次不等式解决问题的步骤:
1.认真审题,分清已知量、未知量及其关系,找出题中不等关系,要抓住题设中的关键字词,如“大于”、“小于”、“不小于”、“不大于”等的含义.
2.设出适当的未知数.
3.根据题中的不等关系,列出不等式.
4.解出所列不等式的解集.
5.写出答案,并检验答案是否符合题意.
知识回顾:
一元一次不等式组
1.定义
不等式组中所有不等式的解集的公共部分叫做不等式组的解集.
2.解一元一次不等式组先分别求出不等式组中每个不等式的解集, 再求出这几个不等式解集的公共部分.
知识回顾:
把几个含有同一个未知数的一次不等式联立在一起,就组成了一个一元一次不等式组.
不等式组解集
知识回顾:
两个一元一次不等式所组成的不等式组的解集情况见下表(其中a<b):
????>????
?
?????
?????
无解
?
复习巩固
解:(1)a?1?0
?
1.用不等式表示:
(1)a与1的差是负数;
(2)x的2倍大于x的三倍与1的和
(3)代数式4x+1的值不小于2
?
(2)2x ?3x+1
(3)4x +1 ?2
复习巩固
(1)a?1?0
?
2.解不等式:
?
(2)2x ?3x+1
(3)4x +1 ?2
解:(1)a?1?0
?
a ? 1
(2) 2x ?3x+1
x ? ?1
?
(3)4x +1 ?2
4x ?1
x ?14
?
??x > 1
?
复习巩固
(1)3?????3<?????15
?
3.解下列不等式,并把它们的解集分别在数轴上表示出来
?
(2)5(x?1) <2(7x+2)
?
解:(1) 3x ??9<?????15
?
(2)?????12<7????+25
?
3x ?????<9?15
?
2????<?6
?
????<?3
?
5x?5 <14x+4
?
?9x <9
?
x >?1
?
-3
-2
-1
3
1
0
2
-5
-4
0
-2
-3
-1
4. 解下列不等式组.
复习巩固
(1)&2????+4>0,????????①&1?2????>0.????????②
?
解:(1)解不等式①,得
????<12
?
????>?2
?
解不等式②,得
不等式组的解集是
?2?
在数轴上表示出不等式组的解集
(2)&?????24>?????13,????????①&2(????+1)>????+3.????????②
?
-2
-1
1
0
12
?
4. 解下列不等式组.
复习巩固
解:(1)解不等式①,得
?????> 2
?
3?????6>4?????4
?
解不等式②,得
不等式组无解
在数轴上表示出不等式组的解集
(2)&?????24>?????13,???????????????①&2(????+1)>????+3.?②
?
?????
2????+2>????+3
?
????>1
?
3(?????2)>4(?????1)
?
-2
-1
1
0
5. 求不等式组&3?????6<4?????,???①&?????1>4?????10.?②的非负整数解.
?
复习巩固
解:解不等式①,得
解不等式②,得
4????<10
?
9>3????
?
????<2.5
?
∴不等式组的解集是
????<3
?
????<2.5
?
∴不等式组的非负整数解是:0,1,2
6.已知不等式组&????>1,???①&?????
复习巩固
不等式组无解,则
-1
1
0
2
在数轴上表示不等式① 的解集
?????1
?
????<1
?
a
变式1.已知不等式组&????>1,???①&?????
复习巩固
不等式组只有一个整数解,则整数解是 2
在数轴上表示不等式① 的解集
2?
1
0
2
3
则a的取值范围是
2?
a
7.已知关于x方程?????2?????????=2的解是正数,求a的取值范围.
?
复习巩固
解:解方程得
由题意得:x > 0
?
?????2????+????=2
?
则?????2>0
?
?????+????=2
?
????=?????2
?
????>2
?
变式1.已知关于x方程?????2?????????=2的解是负数,求正整数a的值.
?
复习巩固
解:解方程得
由题意得:x <0
?
?????2????+????=2
?
则?????2<0
?
?????+????=2
?
????=?????2
?
????<2
?
∵a是正整数
∴a的值是1
变式2.已知关于x,y方程组????+????=2????+1??①?????????=4?????3??②的解x、y是正数,求a的取值范围.
?
复习巩固
解:① +?②得:2????=6?????2
?
由题意得:x >0, y >0
?
则3?????1>0?????+2>0
?
解得 13?
????=3?????1
?
① ??②得:2????=?2????+4
?
????=?????+2
?
变式3.已知关于x,y方程组2????+????=2?3?????①????+2????=4?????????????②的解满足x+y>?2,
求满足条件的m的所有正整数的值.
?
复习巩固
解:① +?②得:3????+3????=6?3????
?
由题意得:x +?????> ?2
?
则2?????>?2
?
????<4
?
????+????=2?????
?
?????>?4
?
∴m的正整数值是1,2,3
8. 某车工计划在15天内至少加工零件408个,前三天每天加工零件24个.此后,该车工平均每天至少需要加工零件多少个,才能在规定的实际完成任务?
复习巩固
解:设以后平均每天加工零件x个
24×3+12?????408
?
根据题意可得:
?????28
?
答:该车工平均每天至少需要加工零件28个
9. 某药店出售消毒免洗手液和口罩,免洗手消毒液每瓶20元,每包口罩5元,该药店有两种优惠方法:
(1)买一瓶消毒免洗手液送一包口罩;(2)按总价的92%付款.
小明需要购买防疫物资做开学准备,需购买4瓶消毒免洗手液、若干包口罩(不少于4包),请问小明买同样多的口罩时,用哪种优惠方法购买省钱?
复习巩固
9. 某药店出售消毒免洗手液和口罩,免洗手消毒液每瓶20元,每包口罩5元,该药店有两种优惠方法:(1)买一瓶消毒免洗手液送一包口罩;(2)按总价的92%付款.
小明需要购买防疫物资做开学准备,需购买4瓶消毒免洗手液、若干包口罩(不少于4包),请问小明买同样多的口罩时,用哪种优惠方法购买省钱?
复习巩固
解:设小明需要购买x(x ? 4)包口罩,
记优惠方法(1)需要花费为y1
①????1>?????2 则5????+60>4.6????+73.6
?
????>34
?
②????1<?????2 则5????+60<4.6????+73.6
?
????<34
?
③????1=?????2?则5????+60=4.6????+73.6
?
????=34
?
答:当小明购买口罩数量大于34包时,选择优惠方式二;当小明购买口罩不少于四包,但小于34包时,选择优惠方式一;当小明买口罩数量等于34包时,两种优惠方式都可以.
4?????<34
?
分析:哪种“省钱”→
比较两种方式总价
→ 缺少口罩数量
→ 设x
y1=20×4+5?????4=5????+60
?
y2 =20×4+5????×0.92=4.6????+73.6
?
记优惠方法(2)需要花费为y2
选择优惠方式二
?
选择优惠方式一
?
两种优惠方式都可以
?
3、在实际问题中利用不等式解决问题.
2、解一元一次不等式(组).
课堂小结:
(1)不等式的性质.
(2)用数轴表示不等式的解集,借助数轴求出不等组解集.
(3)解不等式组口诀.
(4)含参数的不等式相关问题.
找、设、列、解、验、答.
数形结合、转化思想
1、一元一次不等式(组)定义.
第11章 一元一次不等式
谢 谢!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
