人教版数学七年级下册课件:5.1.1相交线(18张PPT)
文档属性
| 名称 | 人教版数学七年级下册课件:5.1.1相交线(18张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 121.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览







文档简介
(共18张PPT)
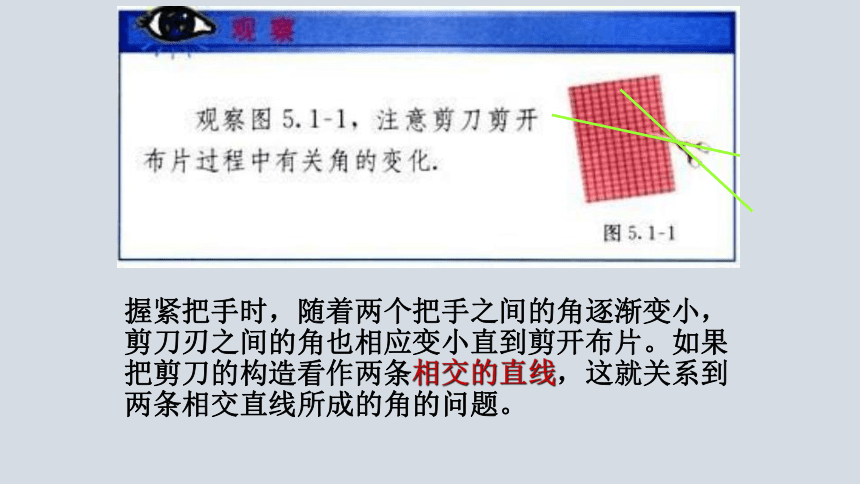
握紧把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角也相应变小直到剪开布片。如果把剪刀的构造看作两条相交的直线,这就关系到两条相交直线所成的角的问题。
5.1.1
相交线
自学指导
自学课本P2-3页练习前,思考下列问题:
1、第2页的探究问题你能回答吗?
2、什么是邻补角?它与补角有什么异同?
你能找出图5.1—2中的邻补角吗?
3、什么是对顶角?请找出图5.1—2中的对顶角。
4、互为邻补角两个角有怎样的数量关系?
对顶角呢?
5、完成P3页练习
任意画两条相交直线,
∠1和∠2
存在怎样的位置关系?
∠2和∠3呢?
O
A
B
C
D
)
(
1
3
4
2
)
(
∠1和∠2有一条公共边OC,另一边互为反向延长线(∠1和∠2互补)。
O
A
B
C
D
)
(
1
3
4
2
)
(
如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角。
如果∠
1
与∠
2
互为邻补角,则∠
1
+∠2=
°;如果∠
1
+∠2
=180,则∠
1
与∠2
是邻补角。
邻补角是有特殊位置的两个互补的角。
邻补角:
不一定
180
图中还有没有邻补角?
∠1和∠3有怎样的位置关系?
O
A
B
C
D
)
(
1
3
4
2
)
(
∠1与∠3有一个公共顶点O,并且两边互为反向延长线,
所以互为对顶角。
对顶角:如果两个角有一个公共点,并且其中一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角。
图中还有没有对顶角?
答:∠2和∠4也是对顶角。
O
A
B
C
D
)
(
1
3
4
2
)
(
对顶角的性质
对顶角相等
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1、有公共顶点
位置关系
邻补角
对顶角
互补
2、有一条公共边
3、另一边互为反向延长线
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
大小关系
相等
B
A
C
D
O
1
2
3
4
1
3
1
2
解:∠2=180°-∠1
=180°-
35°
=145°
∴∠3=∠1=35°
∠4=∠2=145°
若∠1+∠3=50°
呢?
若∠1=
m°呢?
例1、如图,直线a、b相交,∠1=35°,求
∠2、∠3、∠
4的度数。
例2、如图,若∠1:∠2=2:7
,求各角的度数。
解:设∠1=2x°,则∠2=7x
°
根据邻补角的定义,得
2x+7x=180
x=20
则∠1=40°,
∠2=140°
根据对顶角相等,得
∠3=40°,
∠4=140°
1、判断题
有公共顶点且相等的两个角是对顶角。(
)
两条直线相交,有两组对顶角。
(
)
两条直线相交所构成的四个角中有一个角是直角,
那么其余的三个角也是直角。
(
)
×
√
√
2、填空题
一个角的对顶角有
个,邻补角最多有
个,
而补角则可以有
个。
一
两
无数
3、左图中∠AOC的对顶角是
,
邻补角是
.
∠DOB
∠AOD和∠COB
1
A
C
B
D
E
2
)
O
)
4、如图1,∠2与∠3互为邻补角,∠1=∠2,则∠1与∠3的关系为
。
图1
互补
5、三条直线
a、b、c
相交于O点,∠1=40°,∠2=30°,求∠3的度数
c
b
a
1
2
3
4
解:∵∠4
=∠2=30°(对顶角相等
)
∴∠3=180
°-∠4-∠1
=180°-30°-
40°
=110°(补角定义)
6、已知直线AB、CD相交于O点,OA平分∠EOC,∠EOC=70°,求∠BOD和∠BOC的度数。
E
O
A
B
C
D
解:∵OA平分∠EOC
(已知)
∴∠AOC=35°(角平分线定义)
∴∠BOD=∠AOC=35°(对顶角相等)
∠BOC=180°-∠AOC
=108°-35°=145°(邻补角定义)
角的名称
邻补角
对顶角
位置关系
2、有一条公共边
3、另一边互为反向延长线
1、有公共顶点
1、有公共顶点
2、没有公共边
3、两边互为反向延长线
性质
邻补角互补
对顶角相等
相同点
都有一个公共顶点,它们都是成对出现的
不同点
对顶角没有公共边而邻补角有一条公共边;两条直线相交时,一个角的对顶角只有一个,而一个角的邻补角有两个
知识回顾:
课堂检测
1.如图所示,∠1和∠2是对顶角的图形有(
)
A.1个
B.2个
C.3个
D.4个
2.如图.三条直线AB,CD,EF相交于一点O,
∠AOD的对顶角是_____,∠AOC的邻补角是_______,若∠AOC=50°,则BOD=______,∠COB=_______,∠AOE+∠DOB+∠COF=_____。
3.如图,直线a,b,c两两相交,∠1=2∠3,∠2=68°,求∠4的度数
ABC组
课本第7页1、
2、
8、
9题;
D组
课本第7页1、
2、
8题;
作业布置
握紧把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角也相应变小直到剪开布片。如果把剪刀的构造看作两条相交的直线,这就关系到两条相交直线所成的角的问题。
5.1.1
相交线
自学指导
自学课本P2-3页练习前,思考下列问题:
1、第2页的探究问题你能回答吗?
2、什么是邻补角?它与补角有什么异同?
你能找出图5.1—2中的邻补角吗?
3、什么是对顶角?请找出图5.1—2中的对顶角。
4、互为邻补角两个角有怎样的数量关系?
对顶角呢?
5、完成P3页练习
任意画两条相交直线,
∠1和∠2
存在怎样的位置关系?
∠2和∠3呢?
O
A
B
C
D
)
(
1
3
4
2
)
(
∠1和∠2有一条公共边OC,另一边互为反向延长线(∠1和∠2互补)。
O
A
B
C
D
)
(
1
3
4
2
)
(
如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角。
如果∠
1
与∠
2
互为邻补角,则∠
1
+∠2=
°;如果∠
1
+∠2
=180,则∠
1
与∠2
是邻补角。
邻补角是有特殊位置的两个互补的角。
邻补角:
不一定
180
图中还有没有邻补角?
∠1和∠3有怎样的位置关系?
O
A
B
C
D
)
(
1
3
4
2
)
(
∠1与∠3有一个公共顶点O,并且两边互为反向延长线,
所以互为对顶角。
对顶角:如果两个角有一个公共点,并且其中一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角。
图中还有没有对顶角?
答:∠2和∠4也是对顶角。
O
A
B
C
D
)
(
1
3
4
2
)
(
对顶角的性质
对顶角相等
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1、有公共顶点
位置关系
邻补角
对顶角
互补
2、有一条公共边
3、另一边互为反向延长线
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
大小关系
相等
B
A
C
D
O
1
2
3
4
1
3
1
2
解:∠2=180°-∠1
=180°-
35°
=145°
∴∠3=∠1=35°
∠4=∠2=145°
若∠1+∠3=50°
呢?
若∠1=
m°呢?
例1、如图,直线a、b相交,∠1=35°,求
∠2、∠3、∠
4的度数。
例2、如图,若∠1:∠2=2:7
,求各角的度数。
解:设∠1=2x°,则∠2=7x
°
根据邻补角的定义,得
2x+7x=180
x=20
则∠1=40°,
∠2=140°
根据对顶角相等,得
∠3=40°,
∠4=140°
1、判断题
有公共顶点且相等的两个角是对顶角。(
)
两条直线相交,有两组对顶角。
(
)
两条直线相交所构成的四个角中有一个角是直角,
那么其余的三个角也是直角。
(
)
×
√
√
2、填空题
一个角的对顶角有
个,邻补角最多有
个,
而补角则可以有
个。
一
两
无数
3、左图中∠AOC的对顶角是
,
邻补角是
.
∠DOB
∠AOD和∠COB
1
A
C
B
D
E
2
)
O
)
4、如图1,∠2与∠3互为邻补角,∠1=∠2,则∠1与∠3的关系为
。
图1
互补
5、三条直线
a、b、c
相交于O点,∠1=40°,∠2=30°,求∠3的度数
c
b
a
1
2
3
4
解:∵∠4
=∠2=30°(对顶角相等
)
∴∠3=180
°-∠4-∠1
=180°-30°-
40°
=110°(补角定义)
6、已知直线AB、CD相交于O点,OA平分∠EOC,∠EOC=70°,求∠BOD和∠BOC的度数。
E
O
A
B
C
D
解:∵OA平分∠EOC
(已知)
∴∠AOC=35°(角平分线定义)
∴∠BOD=∠AOC=35°(对顶角相等)
∠BOC=180°-∠AOC
=108°-35°=145°(邻补角定义)
角的名称
邻补角
对顶角
位置关系
2、有一条公共边
3、另一边互为反向延长线
1、有公共顶点
1、有公共顶点
2、没有公共边
3、两边互为反向延长线
性质
邻补角互补
对顶角相等
相同点
都有一个公共顶点,它们都是成对出现的
不同点
对顶角没有公共边而邻补角有一条公共边;两条直线相交时,一个角的对顶角只有一个,而一个角的邻补角有两个
知识回顾:
课堂检测
1.如图所示,∠1和∠2是对顶角的图形有(
)
A.1个
B.2个
C.3个
D.4个
2.如图.三条直线AB,CD,EF相交于一点O,
∠AOD的对顶角是_____,∠AOC的邻补角是_______,若∠AOC=50°,则BOD=______,∠COB=_______,∠AOE+∠DOB+∠COF=_____。
3.如图,直线a,b,c两两相交,∠1=2∠3,∠2=68°,求∠4的度数
ABC组
课本第7页1、
2、
8、
9题;
D组
课本第7页1、
2、
8题;
作业布置
