沪科版(2012)初中数学八年级下册 19.1多边形内角和 教案
文档属性
| 名称 | 沪科版(2012)初中数学八年级下册 19.1多边形内角和 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 898.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览

文档简介
19.1 多边形内角和
学习目标
1.理解并掌握多边形的内角、外角等概念;
2.能通过不同方法探索多边形的内角和公式,并会应用它们进行有关计算.(重点、难点)
教学过程
一、情境导入
观察下列图片,你能找出哪些我们熟悉的图形?
今天我们给图形取了一个统一的名字——多边形,那么什么是多边形?如何定义多边形呢?
二、合作探究
探究:多边形内角和
1、
多边形的概念
一个长方形剪去一个角,则它有可能是________边形.
解析:如图所示:沿对角线剪去时,可得到三角形;沿一个顶点和另一边上的一点剪时,可得到四边形;当沿相邻两边上的任意两点(不包含两端点)剪时,可得到五边形.故填:三或四或五.
方法总结:掌握多边形的概念是解决此类问题的关键,但注意分类讨论不要遗漏.
2、
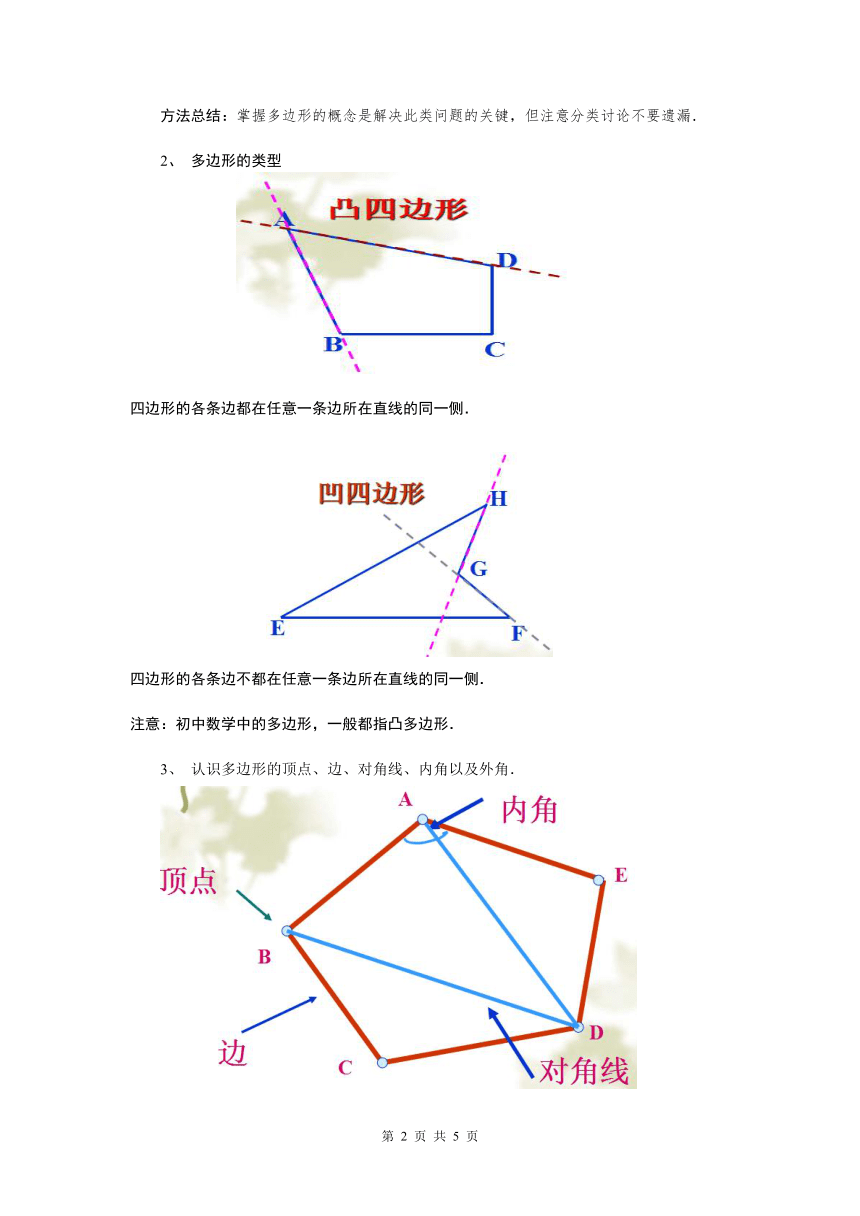
多边形的类型
四边形的各条边都在任意一条边所在直线的同一侧.
四边形的各条边不都在任意一条边所在直线的同一侧.
注意:初中数学中的多边形,一般都指凸多边形.
3、
认识多边形的顶点、边、对角线、内角以及外角.
可表示为:五边形ABCDE或五边形DCBAE等。对角线:连接多边形不相邻的两个顶点的线段。
多边形的内角:多边形中相邻的夹角。
多边形的外角:多边形的边与它的邻边的延长线组成的角。
4、多边形的内角和
回顾:①三角形的内角和是_____.
②正方形、长方形的内角和是_____.猜想:任意四边形的内角和是_____。
验证:画一个任意四边形,用量角器量出它的四个内角的度数,计算内角和。
结论:任意四边形的内角和是3600
怎样证明任意四边形的内角和是3600
?
四边形内角和等于两三角形内角的和:2×180
°=360°
还有其他方法吗?
结论:任意四边形的内角和是3600
你能用以上方法求出五边形的内角和吗?
从顶点A可以画
2
条对角线。五边形被分成了
3
个三角形。那么这个五边形的内角和就是三个三角形的内角和之和:180°×3=540°
六边形呢?
三边形:一个三角形
1x1800
四边形:两个三角形
2x1800
五边形:三个三角形
3x1800
六边形:四个三角形
4x1800
以此类推。。。。。
结论:n边形的内角和等于(n-2).180°
三、知识应用
例1、求十边形的内角和的度数。
解:(10-2)×180°
=1440°
答:十边形的内角和为1440°。
例2、若一个多边形的内角和是1080°,求这个多边形的边数。
解:设这个多边形的边数为n,可列方程
(n-2)×180°=
1080°.
解得n=8
答:这个多边形是八边形。
4、练一练
1、
边形内角和是四边形内角和的2倍。
2、一个五边形的三个内角是直角,另两个内角都是n°,则n=
。
3、多边形的边数每增加1,内角和增加多少度?
4、小明在计算多边形的内角和时求得的度数是1000°,他的答案正确吗?为什么?
5、已知四边形4个内角的度数比是1︰2︰3︰4,那么这个四边形中最大角的度数是
。
5、课堂小结:这节课学习了什么?有哪些收获?
6、作业布置:
P73
练习
第1、2题
P74课外作业
习题第1、5、7题
第
5
页
共
5
页
学习目标
1.理解并掌握多边形的内角、外角等概念;
2.能通过不同方法探索多边形的内角和公式,并会应用它们进行有关计算.(重点、难点)
教学过程
一、情境导入
观察下列图片,你能找出哪些我们熟悉的图形?
今天我们给图形取了一个统一的名字——多边形,那么什么是多边形?如何定义多边形呢?
二、合作探究
探究:多边形内角和
1、
多边形的概念
一个长方形剪去一个角,则它有可能是________边形.
解析:如图所示:沿对角线剪去时,可得到三角形;沿一个顶点和另一边上的一点剪时,可得到四边形;当沿相邻两边上的任意两点(不包含两端点)剪时,可得到五边形.故填:三或四或五.
方法总结:掌握多边形的概念是解决此类问题的关键,但注意分类讨论不要遗漏.
2、
多边形的类型
四边形的各条边都在任意一条边所在直线的同一侧.
四边形的各条边不都在任意一条边所在直线的同一侧.
注意:初中数学中的多边形,一般都指凸多边形.
3、
认识多边形的顶点、边、对角线、内角以及外角.
可表示为:五边形ABCDE或五边形DCBAE等。对角线:连接多边形不相邻的两个顶点的线段。
多边形的内角:多边形中相邻的夹角。
多边形的外角:多边形的边与它的邻边的延长线组成的角。
4、多边形的内角和
回顾:①三角形的内角和是_____.
②正方形、长方形的内角和是_____.猜想:任意四边形的内角和是_____。
验证:画一个任意四边形,用量角器量出它的四个内角的度数,计算内角和。
结论:任意四边形的内角和是3600
怎样证明任意四边形的内角和是3600
?
四边形内角和等于两三角形内角的和:2×180
°=360°
还有其他方法吗?
结论:任意四边形的内角和是3600
你能用以上方法求出五边形的内角和吗?
从顶点A可以画
2
条对角线。五边形被分成了
3
个三角形。那么这个五边形的内角和就是三个三角形的内角和之和:180°×3=540°
六边形呢?
三边形:一个三角形
1x1800
四边形:两个三角形
2x1800
五边形:三个三角形
3x1800
六边形:四个三角形
4x1800
以此类推。。。。。
结论:n边形的内角和等于(n-2).180°
三、知识应用
例1、求十边形的内角和的度数。
解:(10-2)×180°
=1440°
答:十边形的内角和为1440°。
例2、若一个多边形的内角和是1080°,求这个多边形的边数。
解:设这个多边形的边数为n,可列方程
(n-2)×180°=
1080°.
解得n=8
答:这个多边形是八边形。
4、练一练
1、
边形内角和是四边形内角和的2倍。
2、一个五边形的三个内角是直角,另两个内角都是n°,则n=
。
3、多边形的边数每增加1,内角和增加多少度?
4、小明在计算多边形的内角和时求得的度数是1000°,他的答案正确吗?为什么?
5、已知四边形4个内角的度数比是1︰2︰3︰4,那么这个四边形中最大角的度数是
。
5、课堂小结:这节课学习了什么?有哪些收获?
6、作业布置:
P73
练习
第1、2题
P74课外作业
习题第1、5、7题
第
5
页
共
5
页
