2.2.2椭圆的简单几何性质(2)-人教A版高中数学选修2-1课件(18张)
文档属性
| 名称 | 2.2.2椭圆的简单几何性质(2)-人教A版高中数学选修2-1课件(18张) |  | |
| 格式 | ppt | ||
| 文件大小 | 488.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 13:31:27 | ||
图片预览



文档简介
2.2.2椭圆的简单几何性质
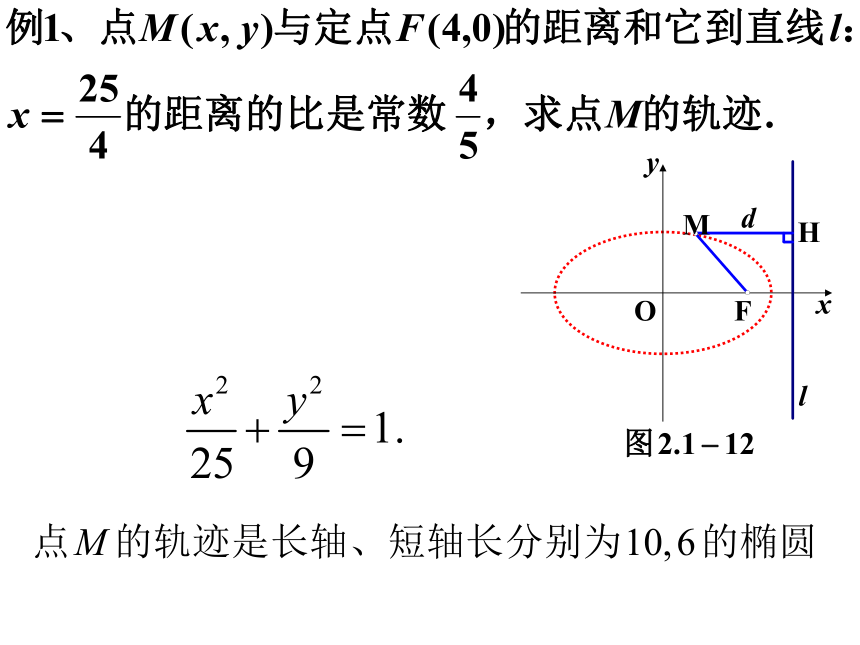
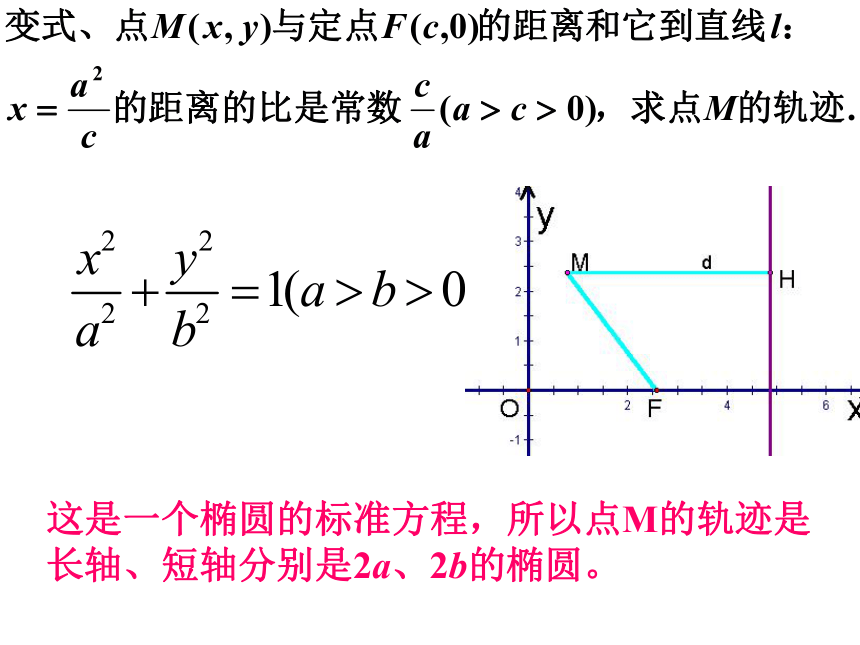
这是一个椭圆的标准方程,所以点M的轨迹是长轴、短轴分别是2a、2b的椭圆。
F
F’
l
I’
x
o
y
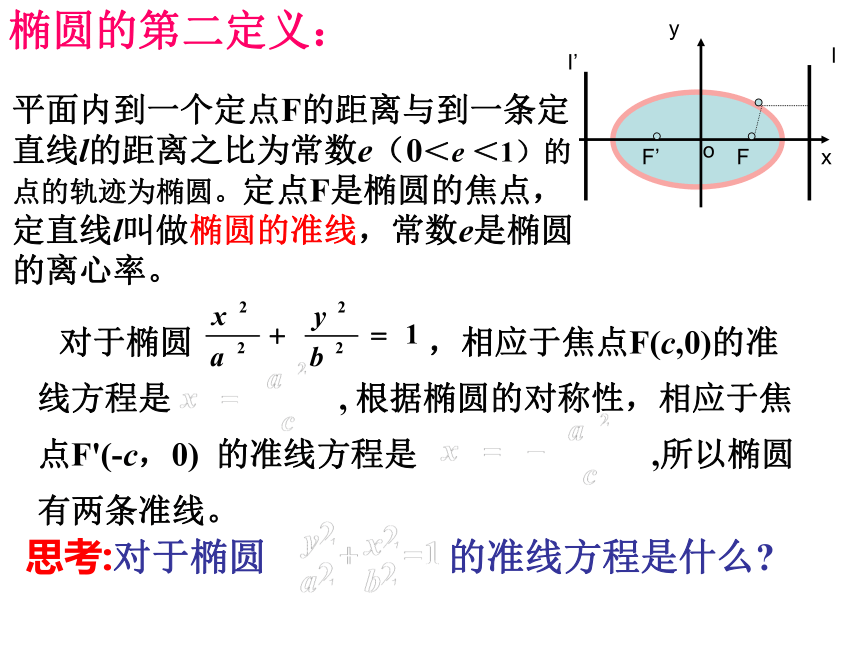
平面内到一个定点F的距离与到一条定直线l的距离之比为常数e(0<e <1)的点的轨迹为椭圆。定点F是椭圆的焦点,定直线l叫做椭圆的准线,常数e是椭圆的离心率。
对于椭圆 ,相应于焦点F(c,0)的准线方程是 , 根据椭圆的对称性,相应于焦点F'(-c,0) 的准线方程是 ,所以椭圆有两条准线。
椭圆的第二定义:
思考:对于椭圆 的准线方程是什么?
点与椭圆的位置关系及判断:
1.点在椭圆上
2.点在椭圆外
3.点在椭圆内
点P(x0,y0)
椭圆
直线和椭圆的位置关系
直线与椭圆的位置关系及判断一:
1.相离:
2.相切:
3.相交:
直线与椭圆无交点
直线与椭圆有且只有一个交点
直线与椭圆有两个交点
几何方法
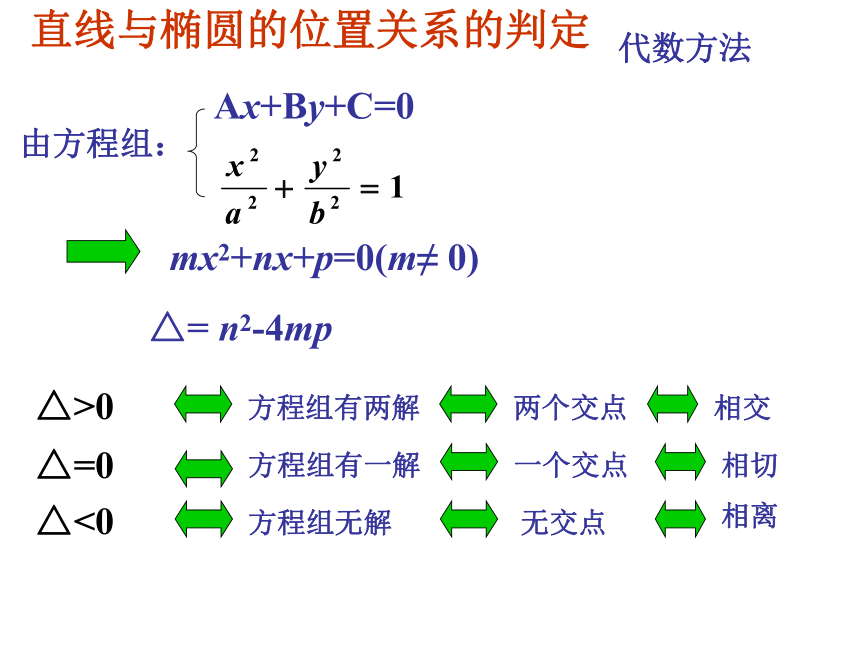
直线与椭圆的位置关系的判定
mx2+nx+p=0(m≠ 0)
Ax+By+C=0
由方程组:
△<0
方程组无解
相离
无交点
△=0
方程组有一解
相切
一个交点
△>0
相交
方程组有两解
两个交点
代数方法
△= n2-4mp
针对练习
针对练习
l
m
m
针对练习
解:设A(x1,y1),B(x2,y2),
∵M(2,1)为AB的中点,
∴x1+x2=4,y1+y2=2
又∵A、B两点在椭圆上,
∴x12+4y12=16,x22+4y22=16,
两式相减得x12-x22+4(y12-y22)=0,
故所求弦AB的方程是x+2y-4=0
针对练习
2、弦长公式:
设直线 l与椭圆C 相交于A( x1 ,y1) ,B( x2,y2 ),
则 |AB|= , 其中k是直线的斜率
1、判断直线与椭圆位置关系的方法:
解方程组消去其中一元得一元二次型方程
△< 0 相离
△= 0 相切
△> 0 相交
3、处理弦中点问题:“点差法”、“韦达定理”
小结
这是一个椭圆的标准方程,所以点M的轨迹是长轴、短轴分别是2a、2b的椭圆。
F
F’
l
I’
x
o
y
平面内到一个定点F的距离与到一条定直线l的距离之比为常数e(0<e <1)的点的轨迹为椭圆。定点F是椭圆的焦点,定直线l叫做椭圆的准线,常数e是椭圆的离心率。
对于椭圆 ,相应于焦点F(c,0)的准线方程是 , 根据椭圆的对称性,相应于焦点F'(-c,0) 的准线方程是 ,所以椭圆有两条准线。
椭圆的第二定义:
思考:对于椭圆 的准线方程是什么?
点与椭圆的位置关系及判断:
1.点在椭圆上
2.点在椭圆外
3.点在椭圆内
点P(x0,y0)
椭圆
直线和椭圆的位置关系
直线与椭圆的位置关系及判断一:
1.相离:
2.相切:
3.相交:
直线与椭圆无交点
直线与椭圆有且只有一个交点
直线与椭圆有两个交点
几何方法
直线与椭圆的位置关系的判定
mx2+nx+p=0(m≠ 0)
Ax+By+C=0
由方程组:
△<0
方程组无解
相离
无交点
△=0
方程组有一解
相切
一个交点
△>0
相交
方程组有两解
两个交点
代数方法
△= n2-4mp
针对练习
针对练习
l
m
m
针对练习
解:设A(x1,y1),B(x2,y2),
∵M(2,1)为AB的中点,
∴x1+x2=4,y1+y2=2
又∵A、B两点在椭圆上,
∴x12+4y12=16,x22+4y22=16,
两式相减得x12-x22+4(y12-y22)=0,
故所求弦AB的方程是x+2y-4=0
针对练习
2、弦长公式:
设直线 l与椭圆C 相交于A( x1 ,y1) ,B( x2,y2 ),
则 |AB|= , 其中k是直线的斜率
1、判断直线与椭圆位置关系的方法:
解方程组消去其中一元得一元二次型方程
△< 0 相离
△= 0 相切
△> 0 相交
3、处理弦中点问题:“点差法”、“韦达定理”
小结
